- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Мультиколлинеарность. Понятие, признаки, методы устранения презентация
Содержание
- 1. Мультиколлинеарность. Понятие, признаки, методы устранения
- 2. Мультиколлинеарность Мультиколлинеарность – совместная, или
- 3. Полная мультиколлинеарность и ее последствия
- 4. Реальная (частичная) мультиколлинеарность Слайд №3
- 5. Внешние признаки реальной мультиколлинеарности неоправданно большие с
- 6. Формальные признаки мультиколлинеарности среди значимых коэффициентов парной
- 7. Анализ внешних признаков мультиколлинеарности Оценка
- 8. Значения оценок коэффициентов уравнения регрессии соответствуют
- 9. 3. Наличие незначимых коэффициентов при переменных Х1,
- 10. Анализ формальных признаков мультиколлинеарности 1. Наличие значимых
- 11. 2. Наличие высоких коэффициентов детерминации Продолжение слайда №7
- 12. 3. Малость определителя матрицы
- 13. Методы устранения мультиколлинеарности 1. . Метод
- 14. Метод пошаговой регрессии Слайд №9 1. Метод пошаговой регрессии с включением переменных
- 15. Продолжение слайда №9
- 16. Продолжение слайда №9
- 17. Метод пошаговой регрессии с исключением переменных Продолжение слайда №9
- 18. Шаг 1. Выбираем первую переменную, включаемую
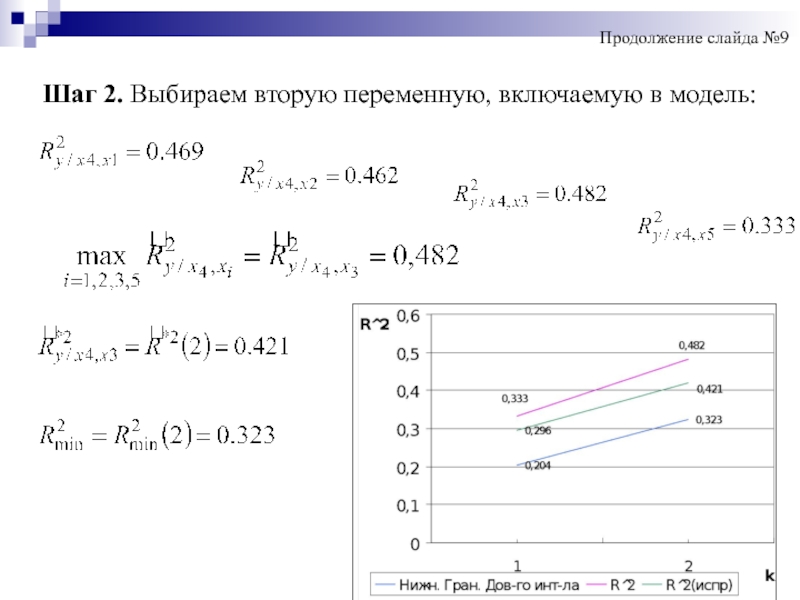
- 19. Шаг 2. Выбираем вторую переменную, включаемую в модель: Продолжение слайда №9
- 20. Шаг 3. Выбираем третью переменную, включаемую в
- 21. - существенные объясняющие переменные
- 22. Метод ридж-регрессии Слайд №10
Мультиколлинеарность Мультиколлинеарность – совместная, или множественная, взаимозависимость объясняющих переменных. Выделяют: Полную мультиколлинеарность - если существует функциональная линейная зависимость между объясняющими переменными, определяется нарушением одного из требований КЛММР, а
Слайд 2Мультиколлинеарность
Мультиколлинеарность – совместная, или множественная,
взаимозависимость объясняющих переменных. Выделяют:
Полную мультиколлинеарность -
если существует функциональная линейная зависимость между объясняющими переменными, определяется нарушением одного из требований КЛММР, а именно, требования к рангу матрицы Х .
Реальная (или частичная) мультиколлинеарность возникает в случаях существования достаточно тесных линейных статистических связей между объясняющими переменными.
Реальная (или частичная) мультиколлинеарность возникает в случаях существования достаточно тесных линейных статистических связей между объясняющими переменными.
Слайд №1
Слайд 3Полная мультиколлинеарность и ее последствия
Когда между объясняющими переменными
существует функциональная зависимость (полная мультиколлинеарность), то матрица объясняющих переменных (матрица Х) вырождена, так как ранг матрицы Х меньше к+1, что в свою очередь, приводит к вырожденности ,а это значит не существует обратная к этой матрице, и следовательно невозможно оценить коэффициенты методом наименьших квадратов.
Слайд №2
Слайд 5Внешние признаки реальной мультиколлинеарности
неоправданно большие с экономической точки зрения значения оценок
коэффициентов уравнения регрессии;
небольшие изменения исходных статистических данных приводит к существенному изменению оценок коэффициентов модели, вплоть до изменения их знаков;
неправильные с экономической точки зрения знаки отдельных коэффициентов регрессии;
среди коэффициентов уравнения регрессии много (может быть все) незначимы, а модель значима;
стандартные отклонения велики на столько, что сравнимы или даже превосходят сами коэффициенты;
доверительные интервалы для коэффициентов уравнения регрессии содержат внутри себя точку ноль.
небольшие изменения исходных статистических данных приводит к существенному изменению оценок коэффициентов модели, вплоть до изменения их знаков;
неправильные с экономической точки зрения знаки отдельных коэффициентов регрессии;
среди коэффициентов уравнения регрессии много (может быть все) незначимы, а модель значима;
стандартные отклонения велики на столько, что сравнимы или даже превосходят сами коэффициенты;
доверительные интервалы для коэффициентов уравнения регрессии содержат внутри себя точку ноль.
Слайд №4
Слайд 6Формальные признаки мультиколлинеарности
среди значимых коэффициентов парной или частной корреляции объясняющих переменных
есть такие, которые по абсолютной величине достаточно велики (превышают 0,75- 0,8);
достаточно высокие значение множественного коэффициента корреляции (детерминации) одной из объясняющих переменных на другие ;
необходимым условием плохой обусловленности является малость определителя матрицы . Если значение оказывается близким к нулю, то свидетельствует о наличии мультиколлинеарности.
достаточным условием плохой обусловленности (мультиколлинеарности) является большое значение числа обусловленности.
достаточно высокие значение множественного коэффициента корреляции (детерминации) одной из объясняющих переменных на другие ;
необходимым условием плохой обусловленности является малость определителя матрицы . Если значение оказывается близким к нулю, то свидетельствует о наличии мультиколлинеарности.
достаточным условием плохой обусловленности (мультиколлинеарности) является большое значение числа обусловленности.
Слайд №5
Слайд 7
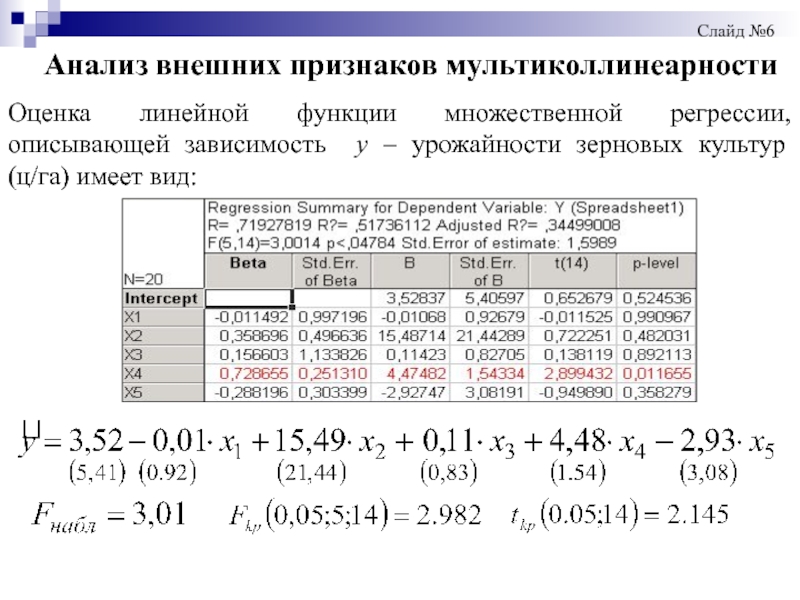
Анализ внешних признаков мультиколлинеарности
Оценка линейной функции множественной регрессии, описывающей зависимость y
– урожайности зерновых культур (ц/га) имеет вид:
Слайд №6
Слайд 8
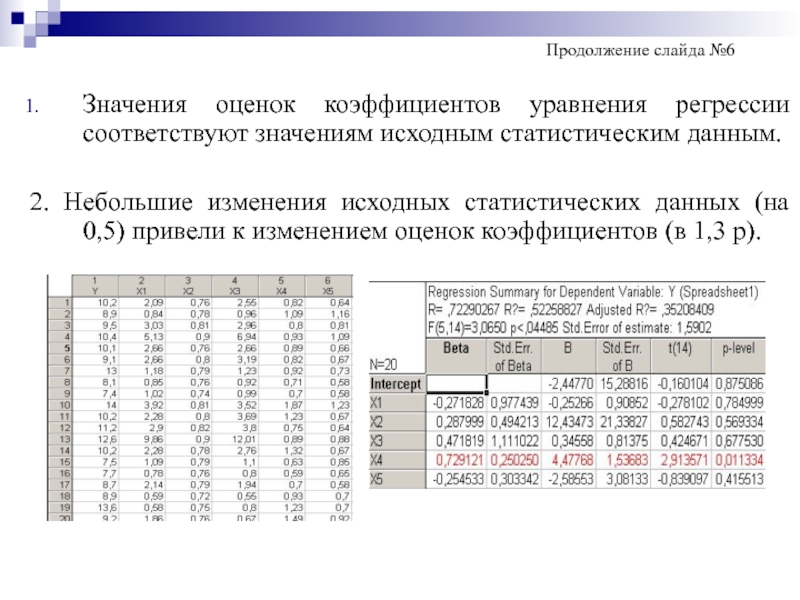
Значения оценок коэффициентов уравнения регрессии соответствуют значениям исходным статистическим данным.
2.
Небольшие изменения исходных статистических данных (на 0,5) привели к изменением оценок коэффициентов (в 1,3 р).
Продолжение слайда №6
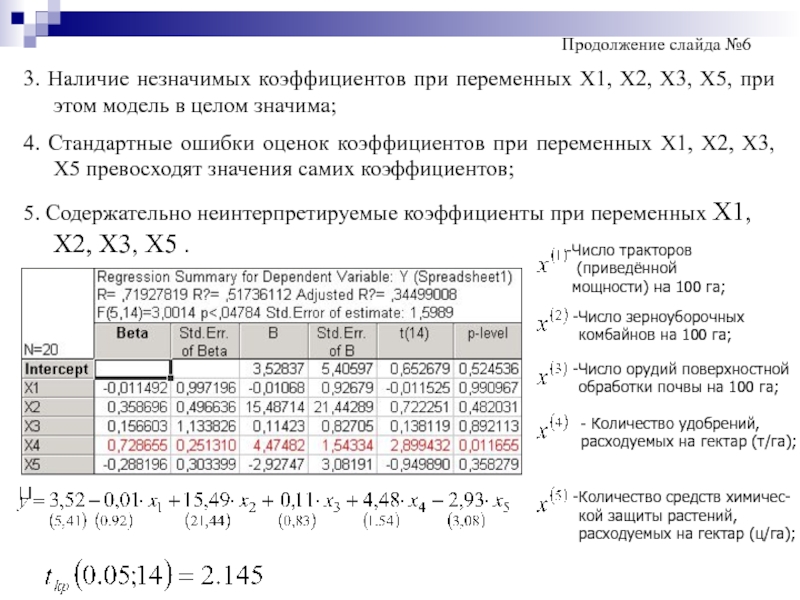
Слайд 93. Наличие незначимых коэффициентов при переменных Х1, Х2, Х3, Х5, при
этом модель в целом значима;
4. Стандартные ошибки оценок коэффициентов при переменных Х1, Х2, Х3, Х5 превосходят значения самих коэффициентов;
5. Содержательно неинтерпретируемые коэффициенты при переменных Х1, Х2, Х3, Х5 .
4. Стандартные ошибки оценок коэффициентов при переменных Х1, Х2, Х3, Х5 превосходят значения самих коэффициентов;
5. Содержательно неинтерпретируемые коэффициенты при переменных Х1, Х2, Х3, Х5 .
Продолжение слайда №6
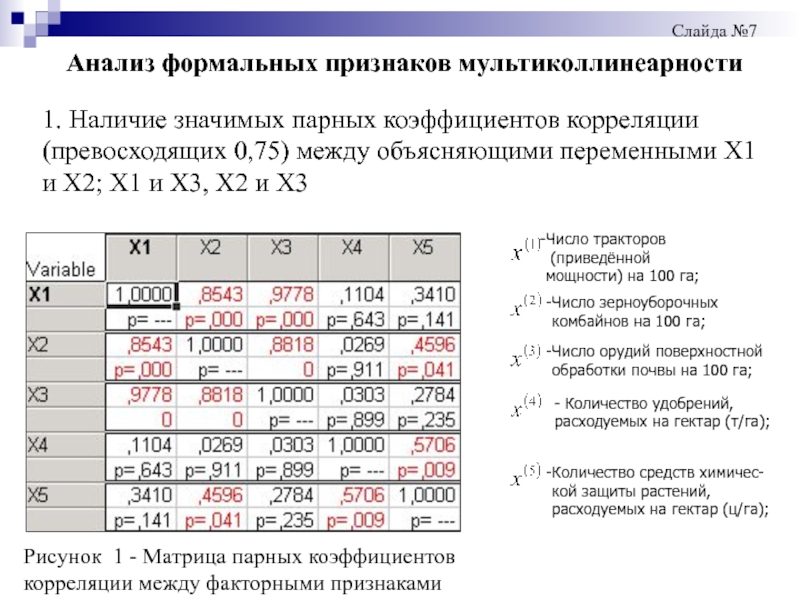
Слайд 10Анализ формальных признаков мультиколлинеарности
1. Наличие значимых парных коэффициентов корреляции (превосходящих 0,75)
между объясняющими переменными Х1 и Х2; Х1 и Х3, Х2 и Х3
Рисунок 1 - Матрица парных коэффициентов
корреляции между факторными признаками
Слайда №7
Слайд 123. Малость определителя матрицы
4. Большое значение числа обусловленности матрицы
Продолжение слайда №7
Слайд 13Методы устранения мультиколлинеарности
1. . Метод пошаговой регрессии :
- с включением
переменных
- с исключением переменных
2. Метод «ридж-регрессии
3. Метод главных компонент
- с исключением переменных
2. Метод «ридж-регрессии
3. Метод главных компонент
Слайда №8
Слайд 18
Шаг 1. Выбираем первую переменную, включаемую в модель:
Поправленный на несмещённость коэффициент
детерминации:
Нижняя граница доверительного интервала
Пример реализации метода пошаговой регрессии
Продолжение слайда №9
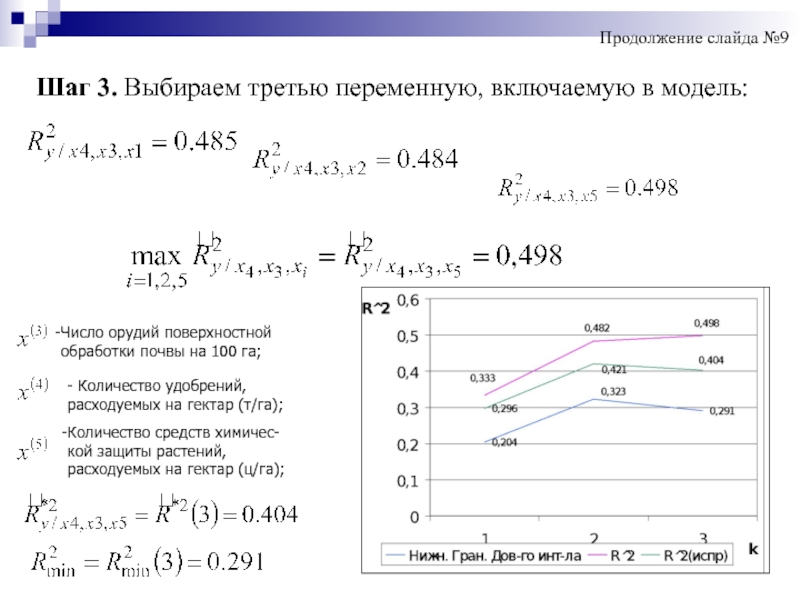
Слайд 20Шаг 3. Выбираем третью переменную, включаемую в модель:
Число орудий поверхностной
обработки
почвы на 100 га;
- Количество удобрений,
расходуемых на гектар (т/га);
Количество средств химичес-
кой защиты растений,
расходуемых на гектар (ц/га);
Продолжение слайда №9
Слайд 21
- существенные объясняющие переменные x3, x4:
Y – Урожайность зерновых культур (ц/га);
Продолжение
слайда №9
