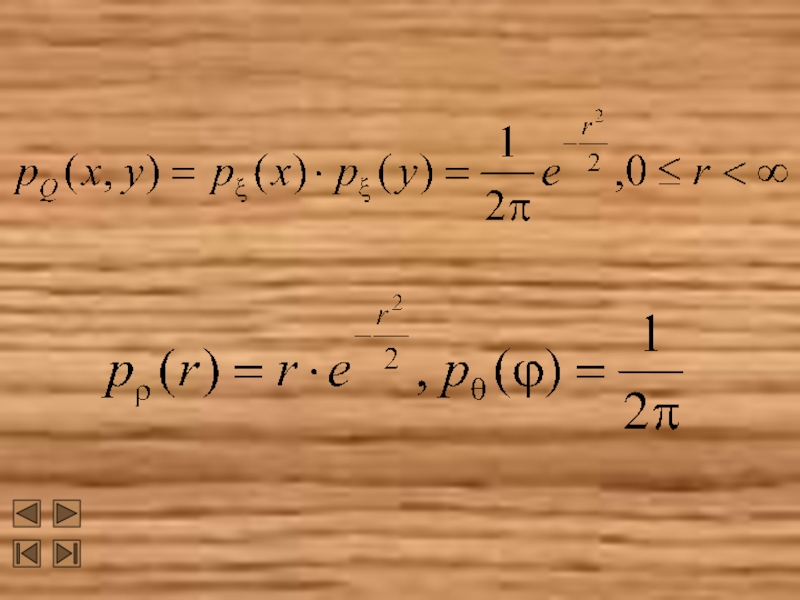- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Моделирование случайных событий презентация
Содержание
- 2. Моделирование случайных событий
- 3. Моделирование случайных событий 3.
- 4. Моделирование случайных событий 4.
- 5. Моделирование непрерывных случайных величин ξ ~ p(x) на (a,b)
- 6. Моделирование непрерывных случайных величин
- 7. Доказательство теоремы 2
- 8. Преобразования случайных величин
- 9. Моделирование n-мерной случайной точки с независимыми
- 10. Моделирование n-мерной случайной точки с независимыми
- 11. Моделирование n-мерной случайной точки с независимыми
- 12. Замена переменных
- 13. Преобразования вида Пусть γ1 и
- 14. Q(ξ, η) имеет плотность Применение полярных координат
- 15. Применение полярных координат
- 16. Якобиан = Применение полярных координат
- 17. Применение полярных координат
- 18. Моделирование нормальной случайной величины Пример: Смоделировать сл.в. ξ~N(0,1)
- 20. Моделирование нормальной случайной величины
- 21. Моделирование нормальной случайной величины
- 22. Метод суперпозиции Ck>0 P(η=k)=Ck
- 23. Метод суперпозиции
- 24. Метод суперпозиции
- 25. Преобразования вида P(γ
- 26. Преобразования вида ξ(n)=-ln(γ1γ2…γn)
- 27. Преобразования вида γ1
- 28. Приближенное моделирование нормального распределения для n=12
- 29. Методы отбора , если QЄB
- 30. Методы отбора ξ=η, если η∈(a`,b`)
- 31. Методы отбора
- 32. Метод Неймана
- 33. Метод Неймана Сл.в. ξ, определенная условием ξ=ξ′, если η’
- 34. Метод Неймана
- 35. Метод Неймана
Моделирование случайных событий ξ ξ Попарно несовместны (A1, A2,…, An), P(Ai)=pi
Слайд 4Моделирование случайных событий
4.
А и В – зависимые
совместные события
Р(А)=рА
Р(В)=рВ Р(АВ)=рАВ
р1=рАВ р2=рА-рАВ
р3=рВ-рАВ
р4=1-рА-рВ+рАВ
Слайд 6Моделирование непрерывных случайных величин
Теорема 2: Сл.в.ξ, удовлетворяющая уравнению
F(ξ)=γ, (2)
имеет плотность распределения p(x).
Доказательство: т.к. функция F(x) строго возрастает в интервале (a,b) от F(a)=0 до F(b)=1, то уравнение (2) имеет единственный корень при каждом γ.
имеет плотность распределения p(x).
Доказательство: т.к. функция F(x) строго возрастает в интервале (a,b) от F(a)=0 до F(b)=1, то уравнение (2) имеет единственный корень при каждом γ.
Слайд 8Преобразования случайных величин
Пример: Экспоненциальная случайная величина ξ
определена на (0, ∞)
с плотностью
p(x)=a*exp(-ax)
p(x)=a*exp(-ax)
Слайд 9Моделирование n-мерной случайной точки
с независимыми координатами
Координаты n-мерной сл. т. Q
Слайд 10Моделирование n-мерной случайной точки
с независимыми координатами
Плотность вероятностей т. Q постоянна
в П:
Пример: Сл.т. Q в декартовых координатах (ξ1,ξ2) р.р. в прямоугольнике П
Слайд 11Моделирование n-мерной случайной точки
с независимыми координатами
Следовательно, ξ1 и ξ2 равномерно
распределены в интервалах (a1,b1), (a2,b2). И эти координаты независимы. Тогда
Тогда
Слайд 13Преобразования вида
Пусть γ1 и γ2 -
два независимых случайных числа.
Могут существовать функции g(x,y) такие,
что случайная величина g(γ1,γ2)
имеет функцию распределения F(x)
Могут существовать функции g(x,y) такие,
что случайная величина g(γ1,γ2)
имеет функцию распределения F(x)
