- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Моделирование систем и процессов. Марковские процессы. (Лекция 3) презентация
Содержание
- 1. Моделирование систем и процессов. Марковские процессы. (Лекция 3)
- 2. Цепочка состояний устройства (системы) Марковская цепь
- 3. Методологические проблемы описания цепочки состояний: В
- 4. Марковские случайные процессы Марковские процессы - для
- 6. Размеченный граф состояний и переходов Граф состояний
- 7. Марковская цепь называется однородной, если переходные вероятности
- 8. Графическое отображение конечной цепи Маркова
- 9. Свойство эргодичности однородной цепи Маркова означает, что
- 10. Дискретные марковские процессы с непрерывным временем: Случайный
- 11. Пуассоновский процесс Стационарный, без последействия и
Цепочка состояний устройства (системы) Марковская цепь – случайный марковский процесс с дискретными состояниями и дискретным временем.
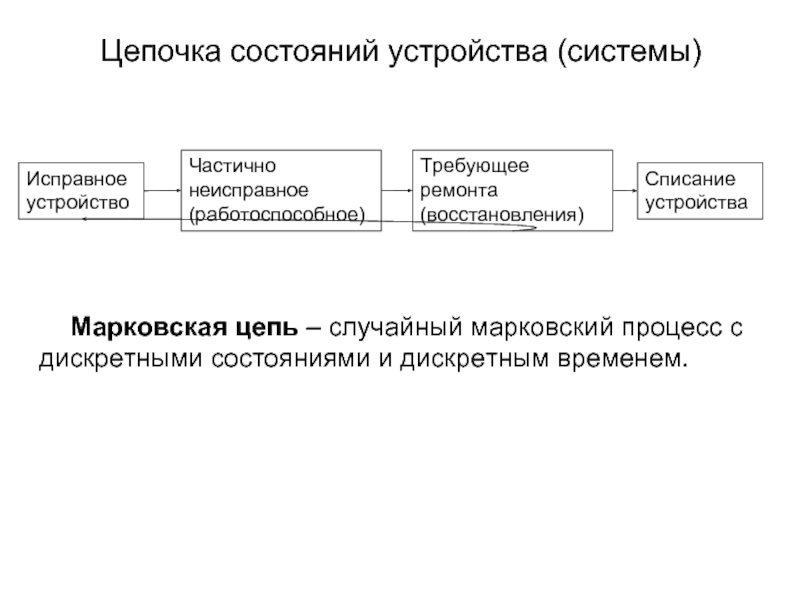
Слайд 2Цепочка состояний устройства (системы)
Марковская цепь – случайный марковский процесс с дискретными
состояниями и дискретным временем.
Слайд 3Методологические проблемы описания цепочки состояний:
В естественных условиях процессы старения происходят непрерывно.
Любое
техническое устройство не работает постоянно, работает с различной нагрузкой.
Системы рассматривается в вероятностной постановке. Переход из одного состояния в другое носит вероятностный характер
Системы рассматривается в вероятностной постановке. Переход из одного состояния в другое носит вероятностный характер
Слайд 4Марковские случайные процессы
Марковские процессы - для каждого момента времени ti вероятность
любого состояния системы в будущем (при t>ti) зависит только от ее состояния в настоящем (при t=ti) и не зависит от того, когда и каким образом система пришла в это состояние.
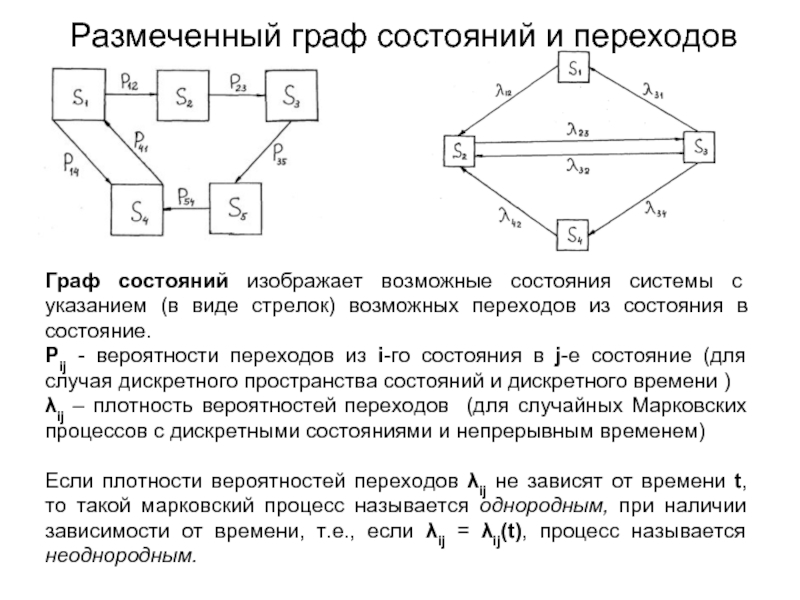
Слайд 6Размеченный граф состояний и переходов
Граф состояний изображает возможные состояния системы с
указанием (в виде стрелок) возможных переходов из состояния в состояние.
Pij - вероятности переходов из i-го состояния в j-e состояние (для случая дискретного пространства состояний и дискретного времени )
λij – плотность вероятностей переходов (для случайных Марковских процессов с дискретными состояниями и непрерывным временем)
Если плотности вероятностей переходов λij не зависят от времени t, то такой марковский процесс называется однородным, при наличии зависимости от времени, т.е., если λij = λij(t), процесс называется неоднородным.
Pij - вероятности переходов из i-го состояния в j-e состояние (для случая дискретного пространства состояний и дискретного времени )
λij – плотность вероятностей переходов (для случайных Марковских процессов с дискретными состояниями и непрерывным временем)
Если плотности вероятностей переходов λij не зависят от времени t, то такой марковский процесс называется однородным, при наличии зависимости от времени, т.е., если λij = λij(t), процесс называется неоднородным.
Слайд 7Марковская цепь называется однородной, если переходные вероятности не зависят от номера
шага (не зависят от момента времени перехода). При зависимости переходных вероятностей от номера шага Марковская цепь называется неоднородной.
Однородная конечная цепь Маркова
Свойство матрицы Рij - сумма членов, стоящих в каждой строке, равна единице
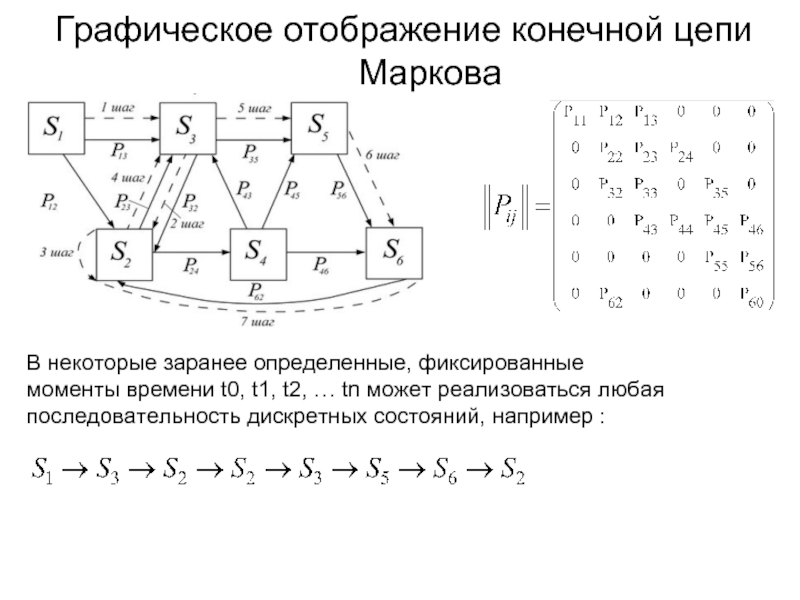
Слайд 8Графическое отображение конечной цепи Маркова
В некоторые заранее определенные, фиксированные моменты времени
t0, t1, t2, … tn может реализоваться любая последовательность дискретных состояний, например :
Слайд 9Свойство эргодичности однородной цепи Маркова означает, что переходные вероятности Pij(t) при
достаточно большом T стремятся независимо от i-го состояния к некоторой стационарной величине.
Другими словами, эргодическая цепь Маркова – это однородная по времени цепь Маркова S(t), обладающая следующим свойством: существуют независимые от i величины:
Это означает, что матрица Pij превращена в матрицу из одной строки
Другими словами, эргодическая цепь Маркова – это однородная по времени цепь Маркова S(t), обладающая следующим свойством: существуют независимые от i величины:
Это означает, что матрица Pij превращена в матрицу из одной строки
Эргодическая цепь Маркова
Слайд 10Дискретные марковские процессы с непрерывным временем:
Случайный поток событий - последовательность однородных
событий, следующих один за другим в какие-то случайные моменты времени.
Интенсивность λ(или «плотность») потока событий- это среднее число событий в единицу времени.
Если λ=const, то поток событий является стационарным , если λ=λ(t) , т.е. зависит от времени, то поток событий является нестационарным.
Экспоненциальный закон распределения:
Интенсивность λ(или «плотность») потока событий- это среднее число событий в единицу времени.
Если λ=const, то поток событий является стационарным , если λ=λ(t) , т.е. зависит от времени, то поток событий является нестационарным.
Экспоненциальный закон распределения:
Слайд 11Пуассоновский процесс
Стационарный, без последействия и ординарный поток событий называется простейшим,
или стационарным пуассоновским потоком. Термин пуассоновский поток означает, что число событий, попадающих на участок τ, распределено по закону Пуассона
