- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Моделирование экономических процессов. Анализ решения моделей презентация
Содержание
- 1. Моделирование экономических процессов. Анализ решения моделей
- 2. Анализ чувствительности решения Должен дать ответ на
- 3. Анализ чувствительности решения Если изменить значение правых
- 4. Математическая модель z = 2000x1 + 2500x2 –> max x1+x2 =200, x2
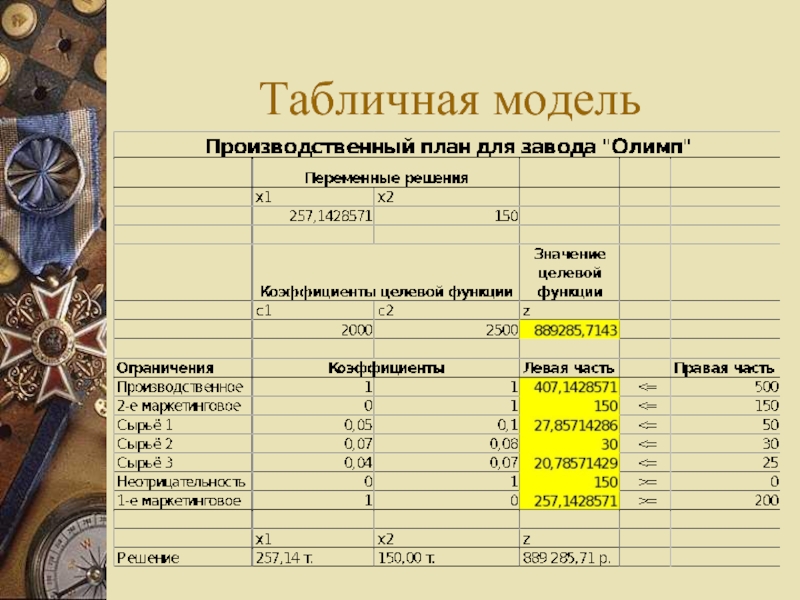
- 5. Табличная модель
- 6. Отчеты «Поиск решения» Для линейных и не
- 7. Отчет по результатам
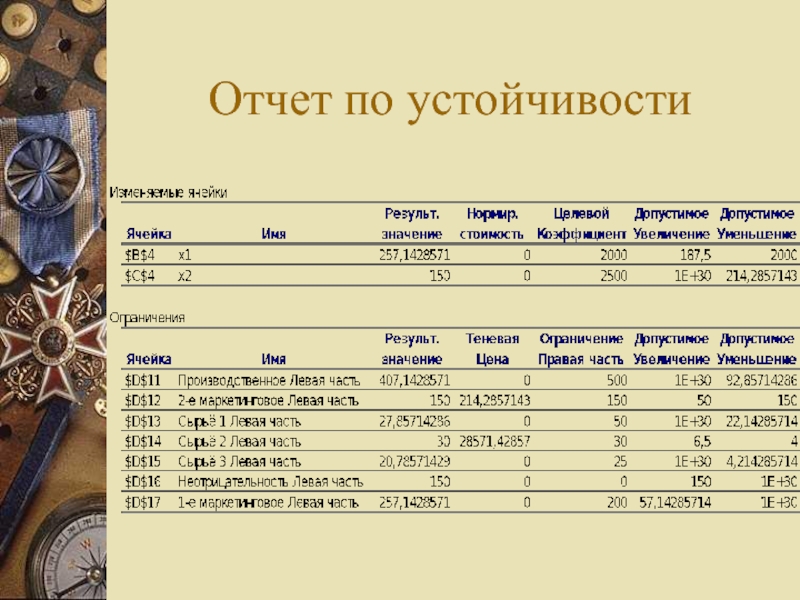
- 8. Отчет по устойчивости
- 9. Таблица «Изменяемые ячейки» Адреса изменяемых ячеек; Их
- 10. Таблица «Изменяемые ячейки» Нормированная стоимость – это
- 11. Таблица «Изменяемые ячейки» Целевой коэффициент – коэффициент,
- 12. Таблица «Ограничения» Адреса ячеек, на значения которых
- 13. Таблица «Ограничения» Теневая цена показывает, на сколько
- 14. Таблица «Ограничения» Значения правых частей ограничений; Значения
- 15. Отчет по пределам В данном отчете показано,
- 16. Сценарии Сценарий – это сохранённые как единое
- 17. Анализ решения целочисленной модели В тех случаях,
- 18. Анализ решения целочисленной модели Решать задачу как
- 19. Анализ решения целочисленной модели Можно считать, что
- 20. Анализ решения целочисленной модели Можно рассматривать результаты
- 21. Анализ решения нелинейной модели Основная проблема анализа
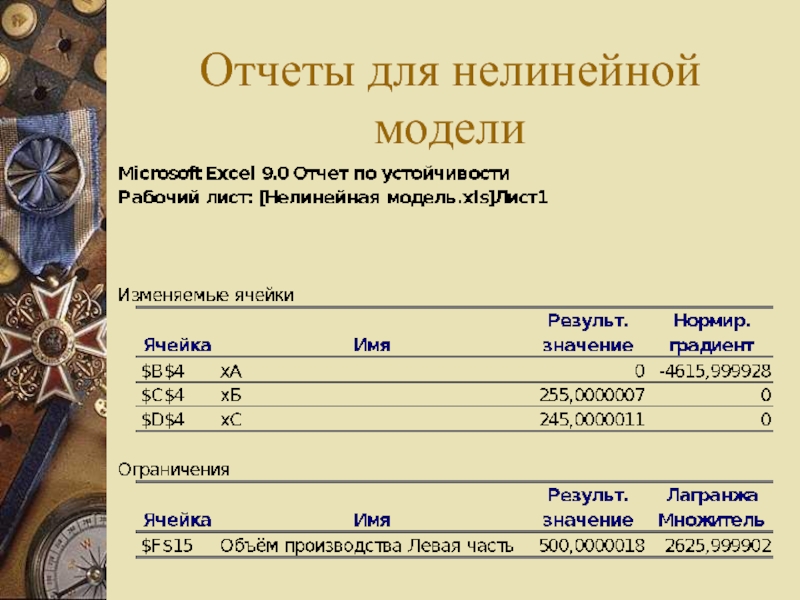
- 22. Отчеты для нелинейной модели
- 23. Отчет по устойчивости для нелинейной модели Нормированный
- 24. Отчет по устойчивости для нелинейной модели Множитель
Слайд 2Анализ чувствительности решения
Должен дать ответ на следующие вопросы:
В каких пределах могут
изменяться параметры модели так, чтобы сохранилось полученное решение?
Какие ограничения связанные (т.е. Лимитируют (сдерживают целевую функцию), а какие ограничения не влияют на решение?
Какие ограничения связанные (т.е. Лимитируют (сдерживают целевую функцию), а какие ограничения не влияют на решение?
Слайд 3Анализ чувствительности решения
Если изменить значение правых частей связанных ограничений, то на
сколько может измениться значение целевой функции?
Если значение какой-то переменной решения равно нулю, то при каких условиях она может принять положительное значение?
Если значение какой-то переменной решения равно нулю, то при каких условиях она может принять положительное значение?
Слайд 6Отчеты «Поиск решения»
Для линейных и не линейных моделей:
Отчет по результатам
Отчет по
устойчивости (разные)
Отчет по пределам
Для целочисленных моделей только отчет по результатам
Отчет по пределам
Для целочисленных моделей только отчет по результатам
Слайд 9Таблица «Изменяемые ячейки»
Адреса изменяемых ячеек;
Их имена (созданные заранее или составленные из
заголовков строк и столбцов, на пересечении которых находятся изменяемые ячейки);
Значение переменных в этих ячейках, найденные средством «Поиск решения»
Значение переменных в этих ячейках, найденные средством «Поиск решения»
Слайд 10Таблица «Изменяемые ячейки»
Нормированная стоимость – это значение равно нулю, если значение
соответствующей переменной находится в границах своего возможного изменения, но не достигает этих границ (учитываются границы, которые задаются явно в виде неравенств типа x>=0 или x<=100). Если переменная равна значению одной из своих явно заданных границ, то значение нормированной стоимости показывает, на сколько изменится значение целевой функции, если значение этой переменной увеличится на единицу.
Слайд 11Таблица «Изменяемые ячейки»
Целевой коэффициент – коэффициент, стоящий при данной изменяемой переменной
в формуле целевой функции;
Значения в столбцах Допустимое увеличение и Допустимое уменьшение показывают, в каких пределах может изменяться целевой коэффициент при условии, что найденные значения переменных останутся неизменными.
Значения в столбцах Допустимое увеличение и Допустимое уменьшение показывают, в каких пределах может изменяться целевой коэффициент при условии, что найденные значения переменных останутся неизменными.
Слайд 12Таблица «Ограничения»
Адреса ячеек, на значения которых наложены ограничения;
Их имена (созданные заранее
или составленные из заголовков строк и столбцов, на пересечении которых находятся изменяемые ячейки);
Значения в этих ячейках, найденные средством «Поиск решения»
Значения в этих ячейках, найденные средством «Поиск решения»
Слайд 13Таблица «Ограничения»
Теневая цена показывает, на сколько изменится значение целевой функции, если
на единицу изменится значение правой части данного ограничения; теневая цена отлична от нуля только тогда, когда данное ограничение в оптимальном решении является связанным
Слайд 14Таблица «Ограничения»
Значения правых частей ограничений;
Значения в столбцах Допустимое увеличение и Допустимое
уменьшение показывают пределы изменения правой части ограничения, в которых действует приведенное значение теневой цены данного ограничения.
Слайд 15Отчет по пределам
В данном отчете показано, в каких пределах с учетом
всех ограничений могут изменяться переменные (значения в столбцах Верхний предел и Нижний предел) и какие при этом значения будет принимать целевая функция (значения в столбцах Целевой результат)
Слайд 16Сценарии
Сценарий – это сохранённые как единое целое значения ячеек рабочего листа,
содержащие значения и формулы. Excel имеет возможность быстрого переключения между различными сценариями. В сценариях сохраняются константы, т.е. Такие значения, которые в ячейки рабочего листа введены напрямую, а не вычислены по формулам. Значения переменных так же считаются константами.
Слайд 17Анализ решения целочисленной модели
В тех случаях, когда дробные значения переменных решения
не имеют смысла, существуют следующие подходы:
Добавить в модель условие целочисленности, которое требует, чтобы одна или несколько переменных решения принимали только целые значения. При этом с помощью Поиск решения можно найти оптимальное решение, но анализировать трудно , т.к. создастся только отчет по устойчивости
Добавить в модель условие целочисленности, которое требует, чтобы одна или несколько переменных решения принимали только целые значения. При этом с помощью Поиск решения можно найти оптимальное решение, но анализировать трудно , т.к. создастся только отчет по устойчивости
Слайд 18Анализ решения целочисленной модели
Решать задачу как обычную линейную модель, а затем
округлить все переменные решения, которые должны быть целыми. Однако, эта тактика может привести к недопустимым или неоптимальным решениям. Если решения обычной и целочисленной моделей близки, то отчет по устойчивости для обычной модели можно использовать для анализа чувствительности решения целочисленной модели
Слайд 19Анализ решения целочисленной модели
Можно считать, что решения линейной модели без условия
целочисленности задают средний уровень производства за какой-то период. Например, решение «ежемесячно производить 2,5 паровоза» можно реализовать следующим образом: каждый нечетный месяц производится 2 паровоза, а половина паровоза переходит на следующий месяц как полуфабрикат; каждый четный месяц производится 3 паровоза.
Слайд 20Анализ решения целочисленной модели
Можно рассматривать результаты решения простой линейной модели только
как ориентиры для планирования, а не как оперативные решения, которые следует реализовывать. В таком случе эти результаты будут служить основой для принятия окончательного решения, которое неизбежно будет учитывать другие факторы реальной ситуации. Весьма вероятно, что эти факторы все равно приведут к отклонению окончательных решений от нецелочисленных решений
Слайд 21Анализ решения нелинейной модели
Основная проблема анализа решений нелинейной модели состоит в
том, что нельзя быть уверенным, что найденное решение действительно оптимальное и что нет других лучших решений. Поэтому следует проводить повторные решения при различных начальных условиях и анализировать наилучшее из найденных решений. Остальные варианты решений могут дать хороший результат по другим критериям (например, меньше затрат)
Слайд 23Отчет по устойчивости для нелинейной модели
Нормированный градиент – это значение равно
нулю, если значение соответствующей переменной находится в границах своего возможного изменения, но не достигает этих границ (учитываются явно заданные границы, например x>=0 x<=100) Если переменная равна значению одной из своих явно заданных границ, то значение нормированного градиента показывает мгновенную скорость изменения целевой функции при изменении значения этой переменной.
Слайд 24Отчет по устойчивости для нелинейной модели
Множитель Лагранжа показывает мгновенную скорость изменения
значения целевой функции при изменении значения правой части данного ограничения. Множитель Лагранжа отличен от нуля только тогда, когда данное ограничение в оптимальном решении является связанным