- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Модели временных рядов. (Лекция 7) презентация
Содержание
- 1. Модели временных рядов. (Лекция 7)
- 2. ПЛАН ЛЕКЦИИ
- 3. ПОНЯТИЕ ВРЕМЕННОГО РЯДА. ОБЩИЙ ВИД МОДЕЛИ ВРЕМЕННОГО
- 4. ПОНЯТИЕ ВРЕМЕННОГО РЯДА. ОБЩИЙ ВИД МОДЕЛИ ВРЕМЕННОГО
- 5. ПОНЯТИЕ ВРЕМЕННОГО РЯДА. ОБЩИЙ ВИД МОДЕЛИ ВРЕМЕННОГО
- 6. ПОНЯТИЕ ВРЕМЕННОГО РЯДА. ОБЩИЙ ВИД МОДЕЛИ
- 7. ПОНЯТИЕ ВРЕМЕННОГО РЯДА. ОБЩИЙ ВИД МОДЕЛИ ВРЕМЕННОГО РЯДА.
- 8. ПОНЯТИЕ ВРЕМЕННОГО РЯДА. ОБЩИЙ ВИД МОДЕЛИ ВРЕМЕННОГО
- 9. ПОНЯТИЕ ВРЕМЕННОГО РЯДА. ОБЩИЙ ВИД МОДЕЛИ ВРЕМЕННОГО
- 10. 2. ПРОВЕРКА ГИПОТЕЗЫ СУЩЕСТВОВАНИЯ ТЕНДЕНЦИИ.
- 11. 2. ПРОВЕРКА ГИПОТЕЗЫ СУЩЕСТВОВАНИЯ ТЕНДЕНЦИИ.
- 12. 2. ПРОВЕРКА ГИПОТЕЗЫ СУЩЕСТВОВАНИЯ ТЕНДЕНЦИИ.
- 13. 2. ПРОВЕРКА ГИПОТЕЗЫ СУЩЕСТВОВАНИЯ ТЕНДЕНЦИИ.
- 14. 2. ПРОВЕРКА ГИПОТЕЗЫ СУЩЕСТВОВАНИЯ ТЕНДЕНЦИИ.
- 15. 3. СТАЦИОНАРНЫЕ ВРЕМЕННЫЕ РЯДЫ И ИХ ХАРАКТЕРИСТИКИ.
- 16. 3. СТАЦИОНАРНЫЕ ВРЕМЕННЫЕ РЯДЫ И ИХ ХАРАКТЕРИСТИКИ.
- 17. 3. СТАЦИОНАРНЫЕ ВРЕМЕННЫЕ РЯДЫ И ИХ ХАРАКТЕРИСТИКИ.
- 18. 3. СТАЦИОНАРНЫЕ ВРЕМЕННЫЕ РЯДЫ И ИХ ХАРАКТЕРИСТИКИ.
- 19. 3. СТАЦИОНАРНЫЕ ВРЕМЕННЫЕ РЯДЫ И ИХ ХАРАКТЕРИСТИКИ.
- 20. 3. СТАЦИОНАРНЫЕ ВРЕМЕННЫЕ РЯДЫ И ИХ ХАРАКТЕРИСТИКИ.
- 21. 3. СТАЦИОНАРНЫЕ ВРЕМЕННЫЕ РЯДЫ И ИХ ХАРАКТЕРИСТИКИ.
- 22. 4. ВЫЯВЛЕНИЕ СТРУКТУРЫ ВРЕМЕННОГО РЯДА.
- 23. 4. ВЫЯВЛЕНИЕ СТРУКТУРЫ ВРЕМЕННОГО РЯДА.
- 24. 4. ВЫЯВЛЕНИЕ СТРУКТУРЫ ВРЕМЕННОГО РЯДА.
- 25. 4. ВЫЯВЛЕНИЕ СТРУКТУРЫ ВРЕМЕННОГО РЯДА.
- 26. 4. ВЫЯВЛЕНИЕ СТРУКТУРЫ ВРЕМЕННОГО РЯДА.
Слайд 3ПОНЯТИЕ ВРЕМЕННОГО РЯДА.
ОБЩИЙ ВИД МОДЕЛИ ВРЕМЕННОГО РЯДА.
Это последовательность наблюдений Y
Временной (динамический) ряд
Слайд 4ПОНЯТИЕ ВРЕМЕННОГО РЯДА.
ОБЩИЙ ВИД МОДЕЛИ ВРЕМЕННОГО РЯДА.
Каждый уровень временного ряда
Отдельные наблюдения называются
уровнями ряда.
Обозначим их
yt (t=1,2,…,n), (1)
где n – число уровней
Длительные (формируют тенденцию ряда)
Кратковременные – циклические колебания
Случайные факторы
Слайд 5ПОНЯТИЕ ВРЕМЕННОГО РЯДА.
ОБЩИЙ ВИД МОДЕЛИ ВРЕМЕННОГО РЯДА.
В большинстве случаев фактический
Слайд 6
ПОНЯТИЕ ВРЕМЕННОГО РЯДА.
ОБЩИЙ ВИД МОДЕЛИ ВРЕМЕННОГО РЯДА.
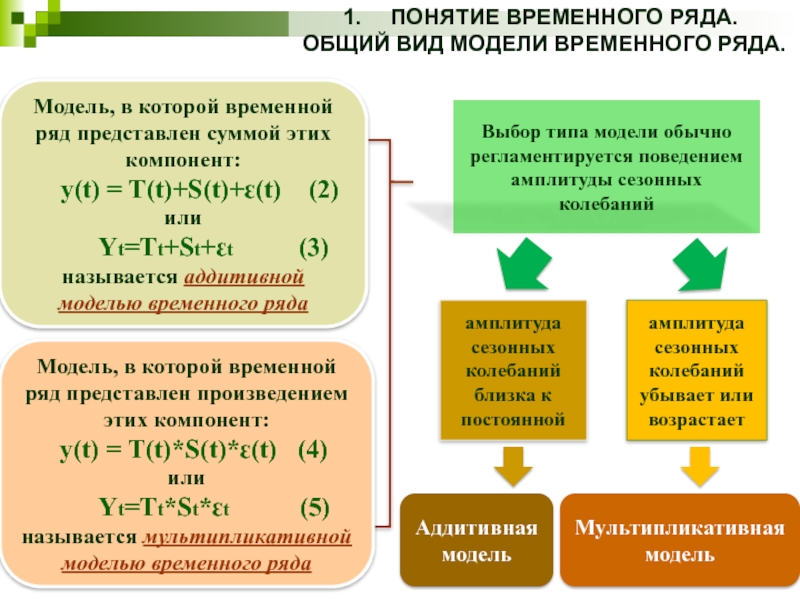
Модель, в которой временной
y(t) = T(t)+S(t)+ԑ(t) (2) или
Yt=Tt+St+ԑt (3)
называется аддитивной моделью временного ряда
Модель, в которой временной ряд представлен произведением этих компонент:
y(t) = T(t)*S(t)*ԑ(t) (4)
или
Yt=Tt*St*ԑt (5)
называется мультипликативной моделью временного ряда
Выбор типа модели обычно регламентируется поведением амплитуды сезонных колебаний
амплитуда сезонных колебаний близка к постоянной
амплитуда сезонных колебаний убывает или возрастает
Аддитивная модель
Мультипликативная модель
Слайд 8ПОНЯТИЕ ВРЕМЕННОГО РЯДА.
ОБЩИЙ ВИД МОДЕЛИ ВРЕМЕННОГО РЯДА.
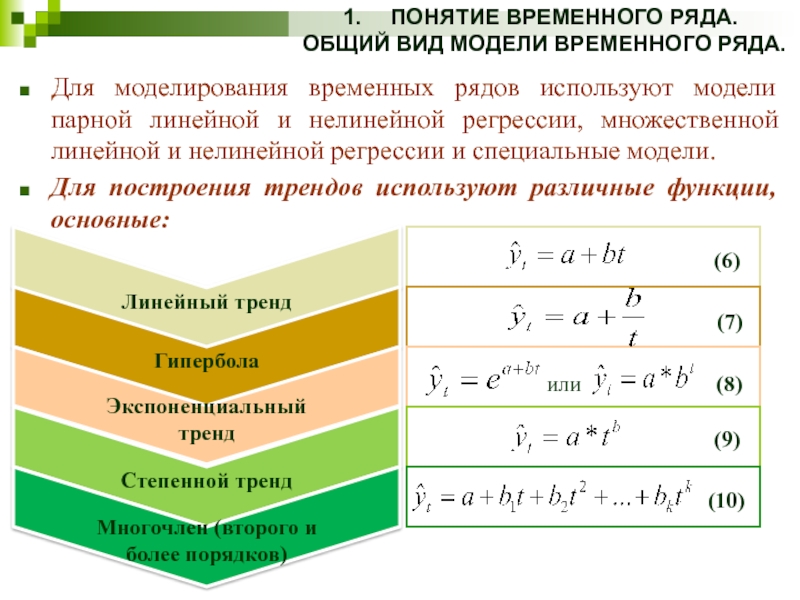
Для моделирования временных рядов
Для построения трендов используют различные функции, основные:
Слайд 9ПОНЯТИЕ ВРЕМЕННОГО РЯДА.
ОБЩИЙ ВИД МОДЕЛИ ВРЕМЕННОГО РЯДА.
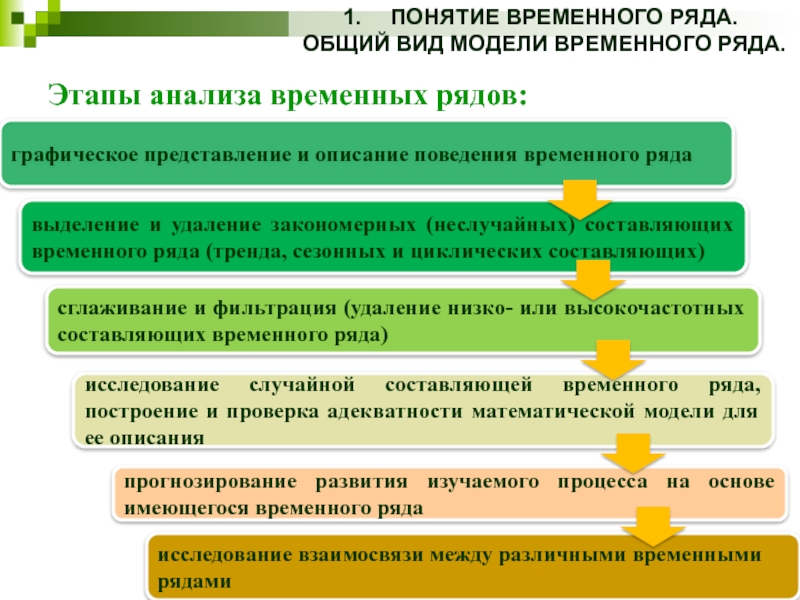
Этапы анализа временных рядов:
графическое
выделение и удаление закономерных (неслучайных) составляющих временного ряда (тренда, сезонных и циклических составляющих)
сглаживание и фильтрация (удаление низко- или высокочастотных составляющих временного ряда)
исследование случайной составляющей временного ряда, построение и проверка адекватности математической модели для ее описания
прогнозирование развития изучаемого процесса на основе имеющегося временного ряда
исследование взаимосвязи между различными временными рядами
Слайд 102. ПРОВЕРКА ГИПОТЕЗЫ СУЩЕСТВОВАНИЯ ТЕНДЕНЦИИ.
Прогнозирование временных рядов целесообразно начинать с
Поэтому в этих случаях необходимо выяснить, существует ли тенденция во временном ряду или она отсутствует.
Слайд 112. ПРОВЕРКА ГИПОТЕЗЫ СУЩЕСТВОВАНИЯ ТЕНДЕНЦИИ.
Для временного ряда рассмотрим критерий «восходящих
(11)
При этом, если последующее наблюдение равно предыдущему, то учитывается только одно наблюдение.
Слайд 122. ПРОВЕРКА ГИПОТЕЗЫ СУЩЕСТВОВАНИЯ ТЕНДЕНЦИИ.
ТАБЛИЦА 1
Квадратные скобки неравенства в (12) означают целую часть числа.
Слайд 132. ПРОВЕРКА ГИПОТЕЗЫ СУЩЕСТВОВАНИЯ ТЕНДЕНЦИИ.
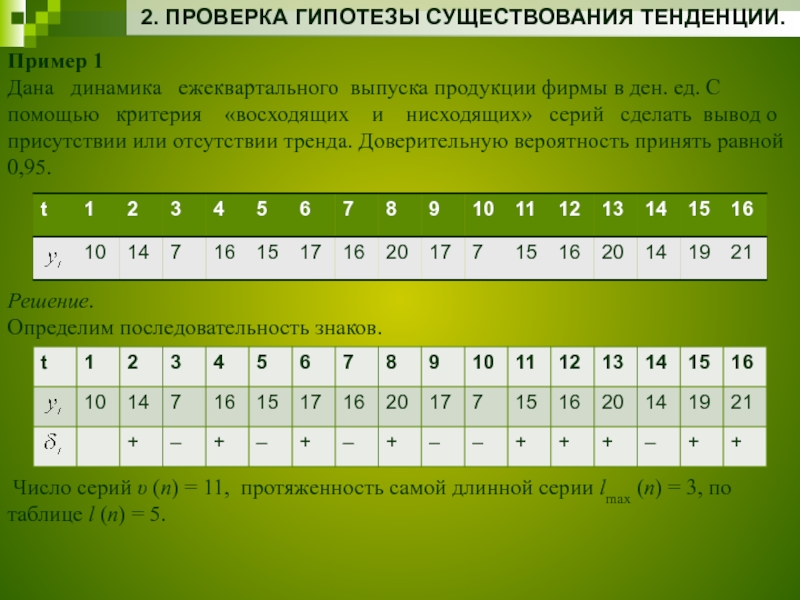
Пример 1
Дана динамика ежеквартального
Слайд 142. ПРОВЕРКА ГИПОТЕЗЫ СУЩЕСТВОВАНИЯ ТЕНДЕНЦИИ.
Запишем систему неравенств:
Оба неравенства выполняются, поэтому
Слайд 153. СТАЦИОНАРНЫЕ ВРЕМЕННЫЕ РЯДЫ И ИХ ХАРАКТЕРИСТИКИ.
Важное значение в анализе временных
Временной ряд yt(t=1,2,…,n) называется стационарным, если совместное распределение вероятностей n наблюдений y1,y2,…,yn такое же, как и n наблюдений y1+r,y2+r,…,yn+r при любых n, t и τ. Другими словами, свойства строго стационарных рядов yt не зависят от момента t, т.е. закон распределения и его числовые характеристики не зависят от t.
Слайд 163. СТАЦИОНАРНЫЕ ВРЕМЕННЫЕ РЯДЫ И ИХ ХАРАКТЕРИСТИКИ.
Следовательно, математическое ожидание My(t)=a, среднее
(14)
(13)
Слайд 173. СТАЦИОНАРНЫЕ ВРЕМЕННЫЕ РЯДЫ И ИХ ХАРАКТЕРИСТИКИ.
Между значениями временного ряда на
Корреляционная зависимость между последовательными уровнями временного ряда называется автокорреляцией уровней временного ряда
Слайд 183. СТАЦИОНАРНЫЕ ВРЕМЕННЫЕ РЯДЫ И ИХ ХАРАКТЕРИСТИКИ.
Степень тесноты связи между последовательностями
(13)
Т.к. p(τ) измеряет корреляцию между членами одного и того же ряда, его называют коэффициентом автокорреляции, а зависимость p(τ) – автокорреляционной функцией.
Слайд 193. СТАЦИОНАРНЫЕ ВРЕМЕННЫЕ РЯДЫ И ИХ ХАРАКТЕРИСТИКИ.
Статистической оценкой p(τ) является выборочный коэффициент автокорреляции r(τ), определяемый по формуле:
Слайд 203. СТАЦИОНАРНЫЕ ВРЕМЕННЫЕ РЯДЫ И ИХ ХАРАКТЕРИСТИКИ.
При расчете r(τ) следует помнить,
Слайд 213. СТАЦИОНАРНЫЕ ВРЕМЕННЫЕ РЯДЫ И ИХ ХАРАКТЕРИСТИКИ.
Наряду с автокорреляционной функцией при
Слайд 234. ВЫЯВЛЕНИЕ СТРУКТУРЫ ВРЕМЕННОГО РЯДА.
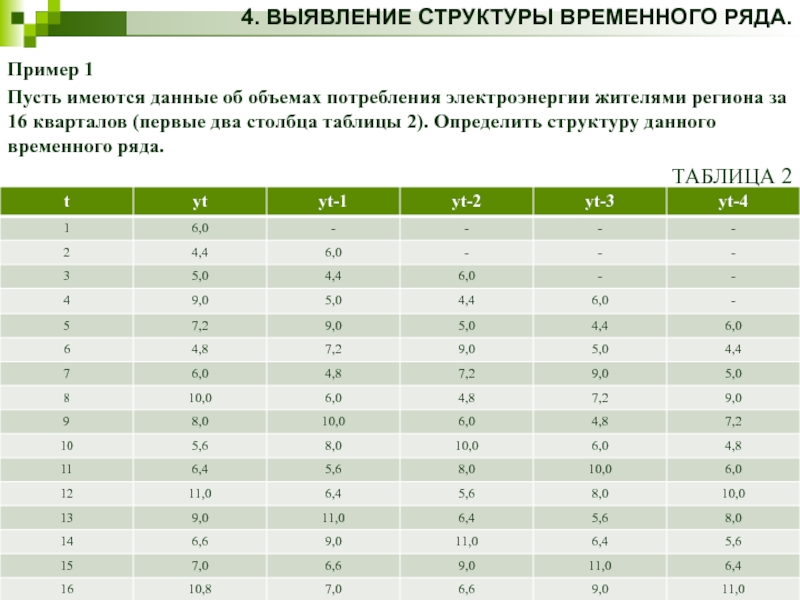
Пример 1
Пусть имеются данные об объемах потребления
ТАБЛИЦА 2
Слайд 244. ВЫЯВЛЕНИЕ СТРУКТУРЫ ВРЕМЕННОГО РЯДА.
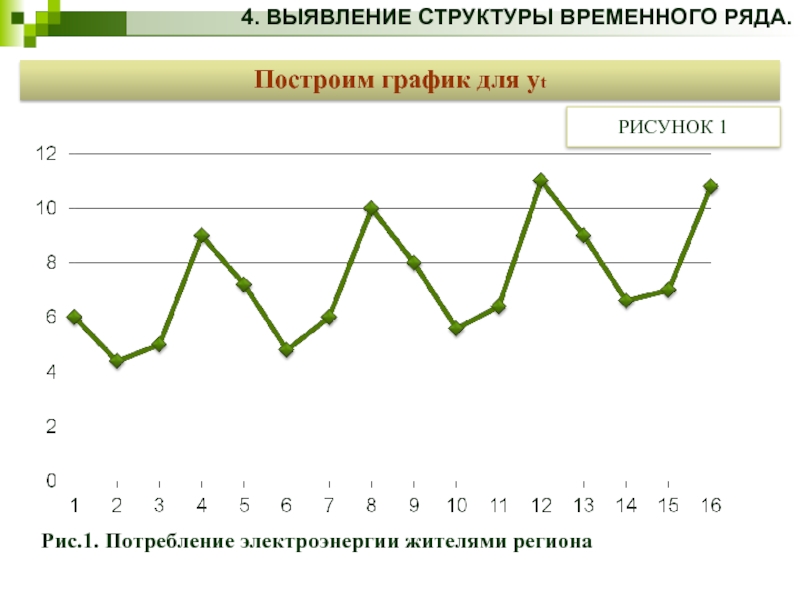
Рис.1. Потребление электроэнергии жителями региона
Построим график для
РИСУНОК 1
Слайд 264. ВЫЯВЛЕНИЕ СТРУКТУРЫ ВРЕМЕННОГО РЯДА.
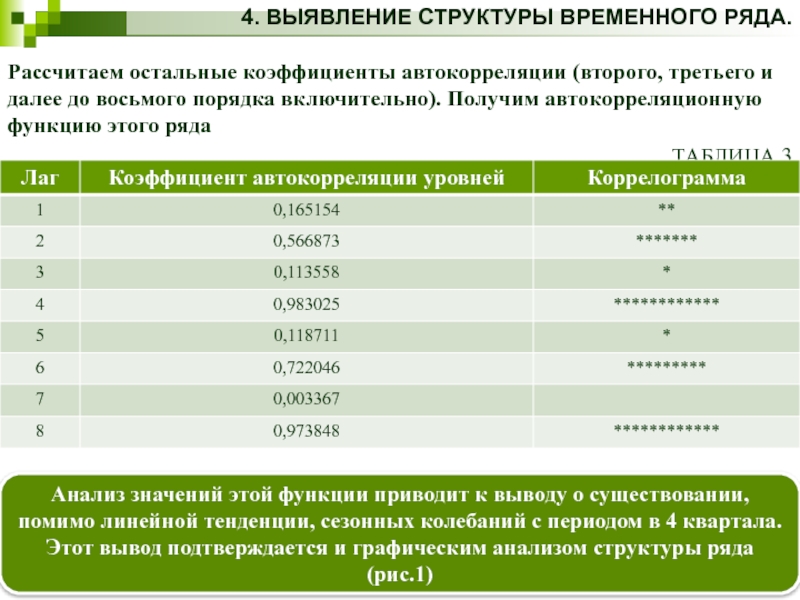
Рассчитаем остальные коэффициенты автокорреляции (второго, третьего и
ТАБЛИЦА 3
Анализ значений этой функции приводит к выводу о существовании, помимо линейной тенденции, сезонных колебаний с периодом в 4 квартала. Этот вывод подтверждается и графическим анализом структуры ряда (рис.1)