- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Множества. Операции над множествами презентация
Содержание
- 1. Множества. Операции над множествами
- 2. Множество – совокупность объектов, объединенных по
- 3. Элементы множества Объекты, из которых образовано множество,
- 4. Виды множеств: Дискретные множества(прерывные)- имеют отдельные элементы.
- 5. Множество четырехугольников Пространственные тела 1, 2, 3,
- 6. множество людей на Солнце множество прямых углов
- 7. Обозначения некоторых числовых множеств:
- 8. Способы задания множеств Перечислением элементов (подходит
- 9. Характеристическое свойство Характеристическое свойство – это такое
- 10. подмножество Множество В является подмножеством множества А
- 11. Круги Эйлера Круги Эйлера – это особые
- 12. Суммой, или объединением произвольного конечного или бесконечного
- 13. ОБЪЕДИНЕНИЕ МНОЖЕСТВ
- 14. Пересечением любого конечного или бесконечного множества множеств
- 15. ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ
- 16. Вычитание множеств Разностью множеств А и В
- 17. Декартово произведение множеств Декартовым произведением множеств А
- 18. Изображение декартова произведения при помощи графа
- 19. Изображение декартова произведения на координатной плоскости
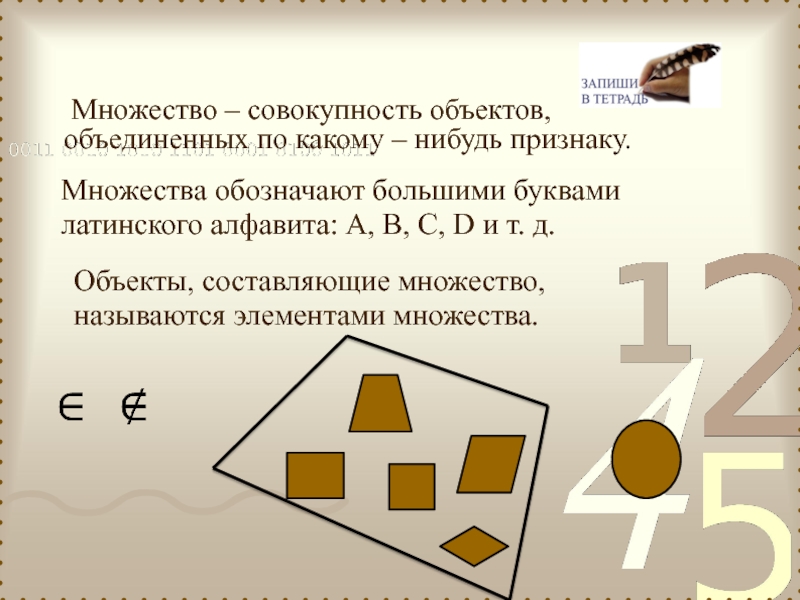
Слайд 2 Множество – совокупность объектов, объединенных по какому – нибудь признаку.
Объекты, составляющие множество, называются элементами множества.
Множества обозначают большими буквами латинского алфавита: А, В, С, D и т. д.
Слайд 3Элементы множества
Объекты, из которых образовано множество, называются элементами.
Элементы множества принято обозначать
Если элемент х принадлежит множеству М, то записывают х О М, если не принадлежит – x П M
Слайд 4Виды множеств:
Дискретные множества(прерывные)- имеют отдельные элементы. Путём счёта распознаются.
Непрерывные множества- нет
Конечные множества- состоят из конечного числа элементов, когда можно пересчитать все элементы множества.
Бесконечные множества- когда невозможно пересчитать все элементы множества.
Упорядочные множества. Элемент из множества предшествует или следует за другим. Множество натуральных чисел, расположенных в виде натурального ряда.
Неупорядочные множества. Любое неупорядочное множество можно упорядочить.
Слайд 5Множество четырехугольников
Пространственные тела
1, 2, 3, 4, 5, 6, 7, 8, 9,
Квадраты чисел
Цифры десятичной системы счисления
10, 12, 14, 16 … 96, 98
Слайд 6множество людей на Солнце
множество прямых углов равностороннего треугольника
множество точек пересечения двух
Пустое множество- множество, не содержащее ни одного элемента.
Слайд 7 Обозначения некоторых числовых множеств:
N – множество натуральных
Z – множество целых чисел;
Q – множество рациональных чисел;
I - множество иррациональных чисел;
R – множество действительных чисел.
Слайд 8Способы задания множеств
Перечислением элементов (подходит для конечных множеств).
Указать характеристическое свойство
С помощью изображения :
На луче
В виде графика
С помощью кругов Эйлера. В основном используется при выполнении действий с множествами или демонстрации их отношений.
Слайд 9Характеристическое свойство
Характеристическое свойство – это такое свойство, которым обладает каждый элемент,
Этот способ задания множеств является общим и для конечных множеств, и для бесконечных.
«Множество А натуральных чисел, меньших 7»: А = {x | x ∈ N и x<7}
Слайд 10подмножество
Множество В является подмножеством множества А (В ⊂ А), если каждый
Отношения между множествами наглядно представляют при помощи кругов Эйлера
Слайд 11Круги Эйлера
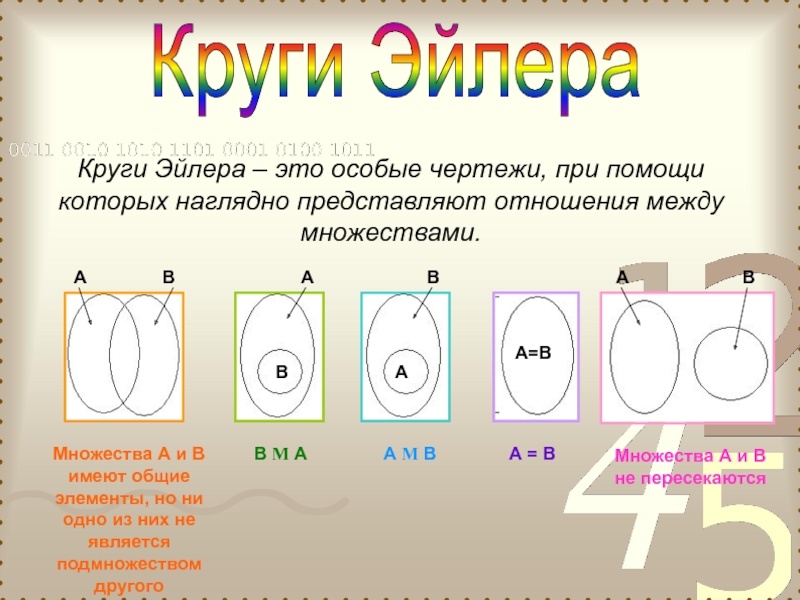
Круги Эйлера – это особые чертежи, при помощи которых наглядно
Множества А и В имеют общие элементы, но ни одно из них не является подмножеством другого
В М А
А М В
А = В
Множества А и В не пересекаются
А
В
А
А
А
В
В
В
А=В
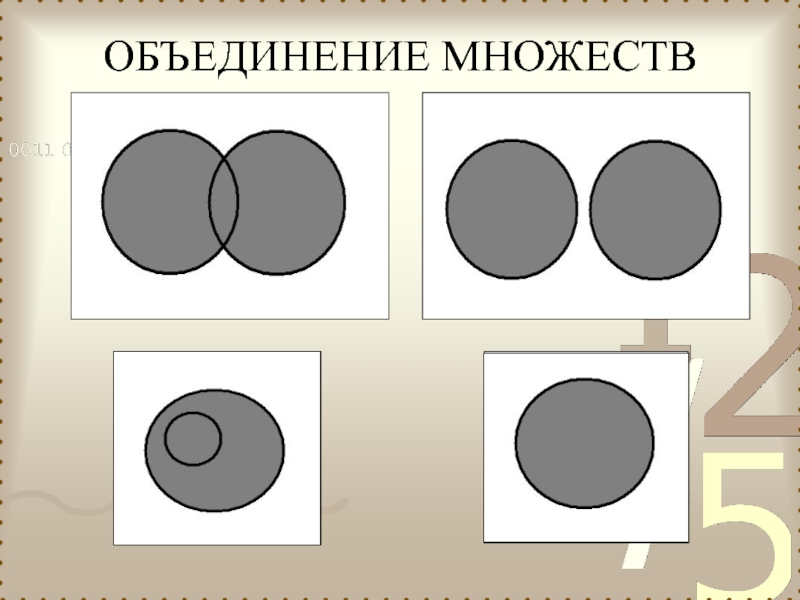
Слайд 12Суммой, или объединением произвольного конечного или бесконечного множества множеств называется множество,
Объединение множеств обозначается
П р и м е р : {1,2,3} {2,3,4} = {1,2,3,4}.
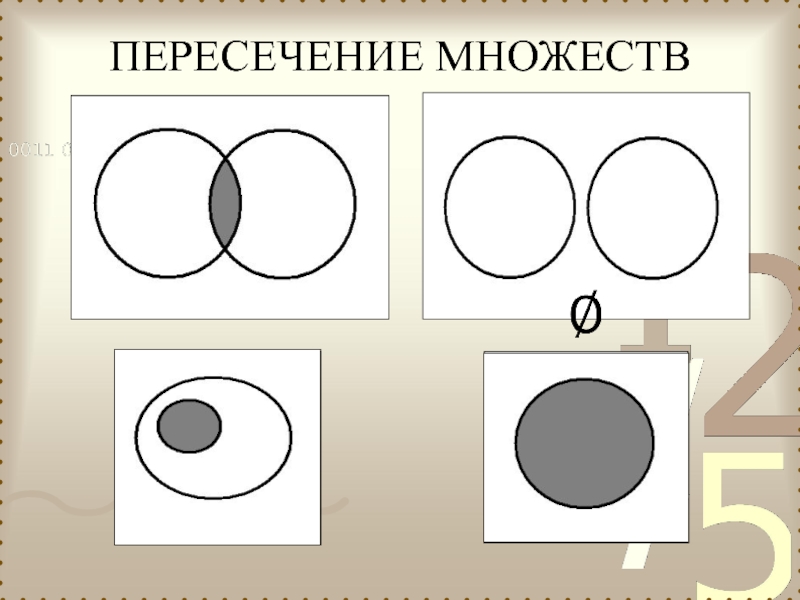
Слайд 14Пересечением любого конечного или бесконечного множества множеств называется множество, состоящее из
Пересечение множеств обозначается
П р и м е р : {1,2,3} {2,3,4} = {2,3}
Слайд 16Вычитание множеств
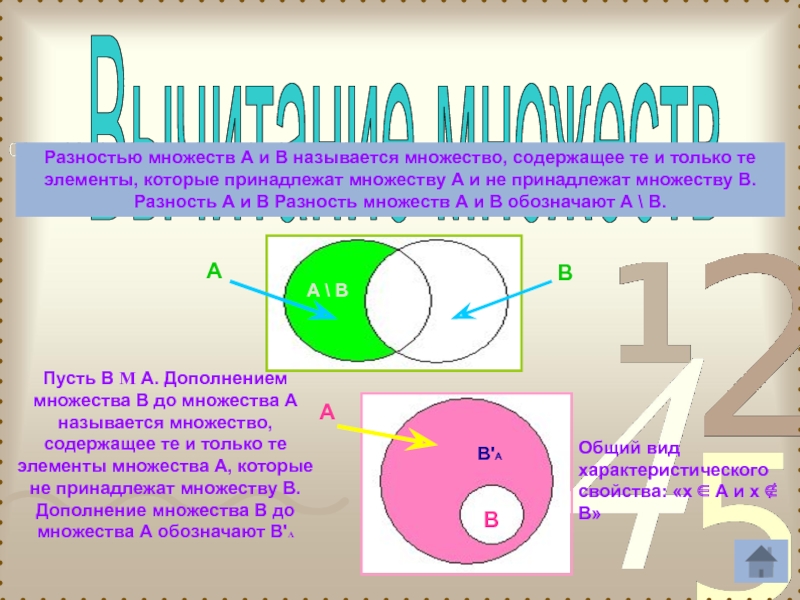
Разностью множеств А и В называется множество, содержащее те и
А
В
А \ В
Пусть В М А. Дополнением множества В до множества А называется множество, содержащее те и только те элементы множества А, которые не принадлежат множеству В. Дополнение множества В до множества А обозначают В'А
А
В
В'А
Общий вид характеристического свойства: «x ∈ А и x ∉ В»
Слайд 17Декартово произведение множеств
Декартовым произведением множеств А и В называется множество всех
Операцию нахождения декартова произведения множеств называют декартовым умножением.
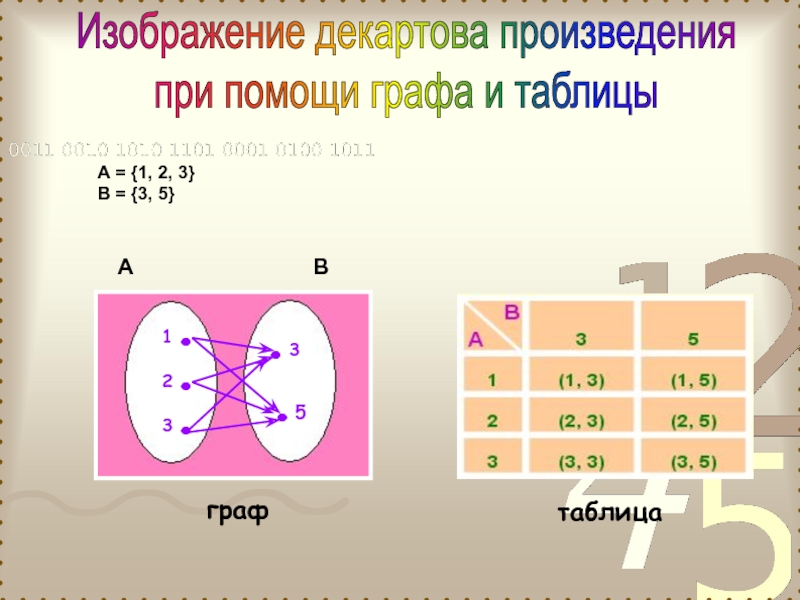
Если множества А и В конечны и содержат небольшое число элементов, можно изобразить декартово произведение этих множеств при помощи графа или таблицы.
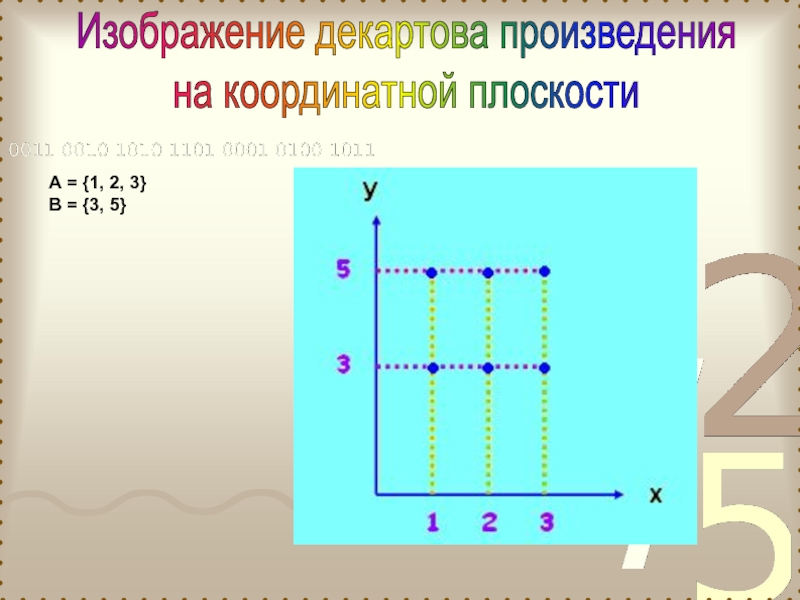
Декартово произведение двух числовых множеств (конечных и бесконечных) можно изображать на координатной плоскости.
Слайд 18Изображение декартова произведения
при помощи графа и таблицы
А = {1, 2,
В = {3, 5}
А
В
1.
2.
3.
.3
.5
граф
таблица