- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Множества и операции над ними презентация
Содержание
- 1. Множества и операции над ними
- 2. Множество – это совокупность определенных различаемых
- 3. Георг Кантор определил множество так: Множество – это многое, мыслимое как целое.
- 4. Например: - множество всех станций Московского метро; - множество
- 5. множество всех натуральных чисел: 1, 2, 3,
- 6. Множество обозначают заглавными буквами, а его
- 7. Множество, не содержащее элементов, называется пустым множеством
- 8. Способы задания множества: Перечисление всех элементов
- 9. Выясним далее, какие из приведенных определений верные:
- 10. Порождающая процедура Описывает способ получения элементов множества
- 11. Множество натуральных
- 12. Задание множества описанием его элементов (разрешающая процедура)
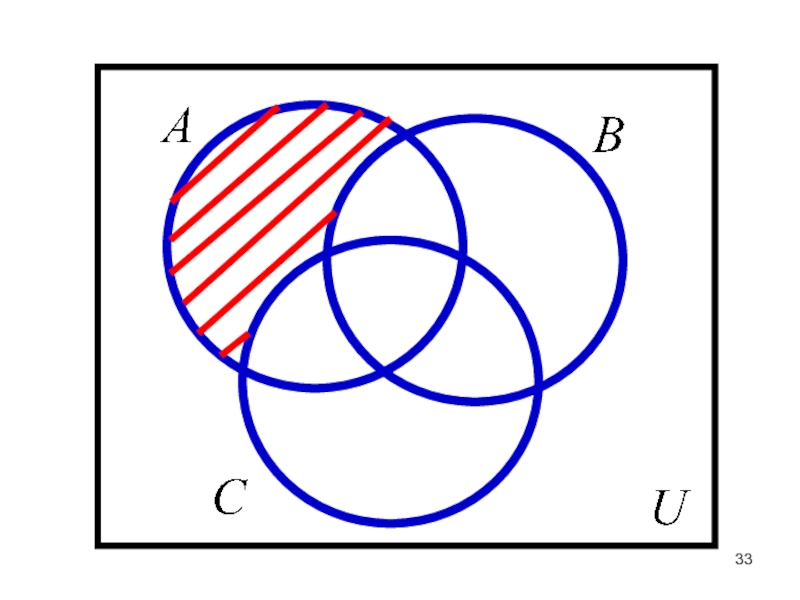
- 13. Множество А называют подмножеством множества В (обозначается
- 14. Множества А и В называют равными
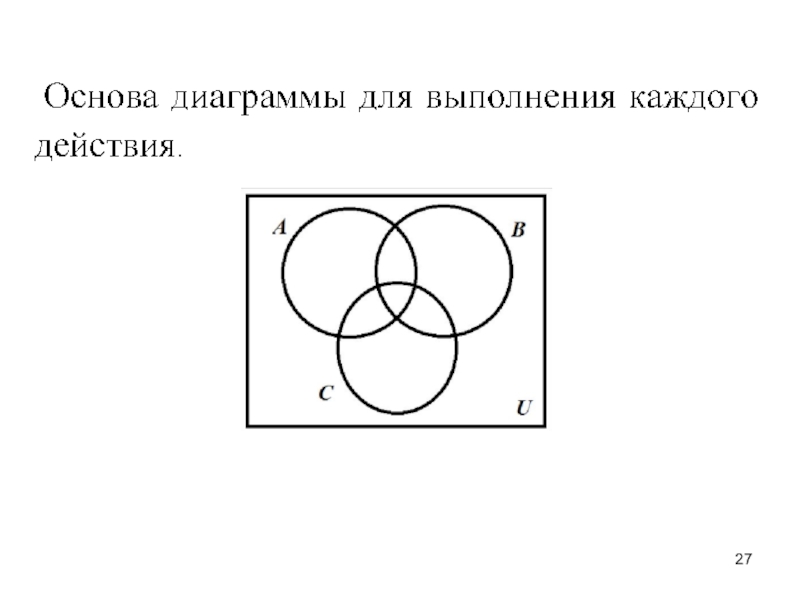
- 15. Множество U называется универсальным
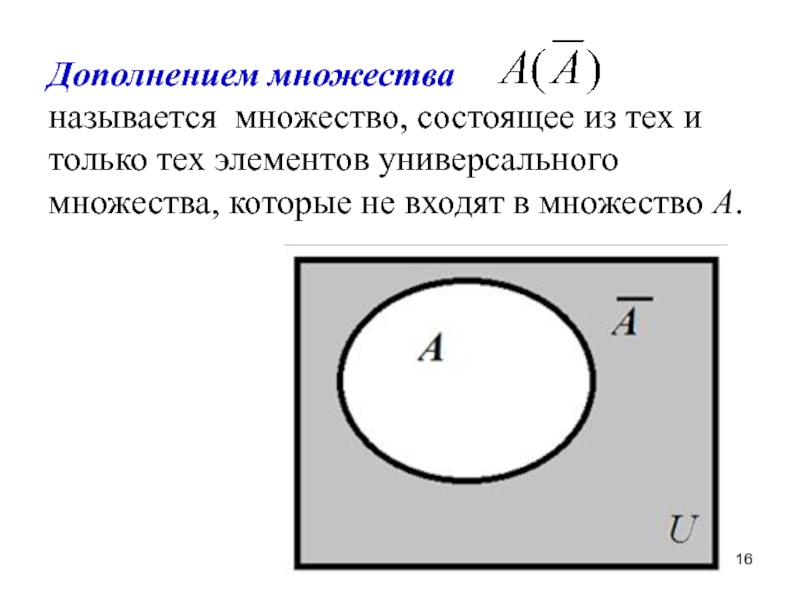
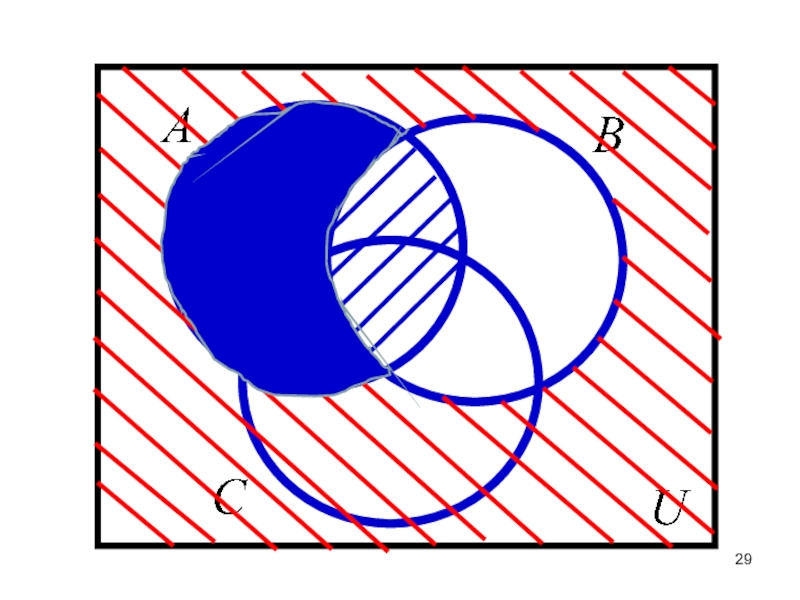
- 16. Дополнением множества
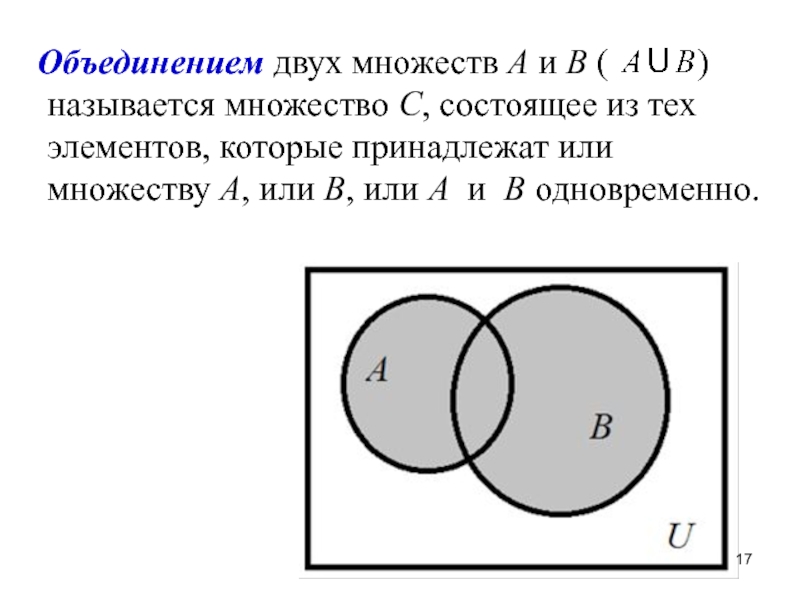
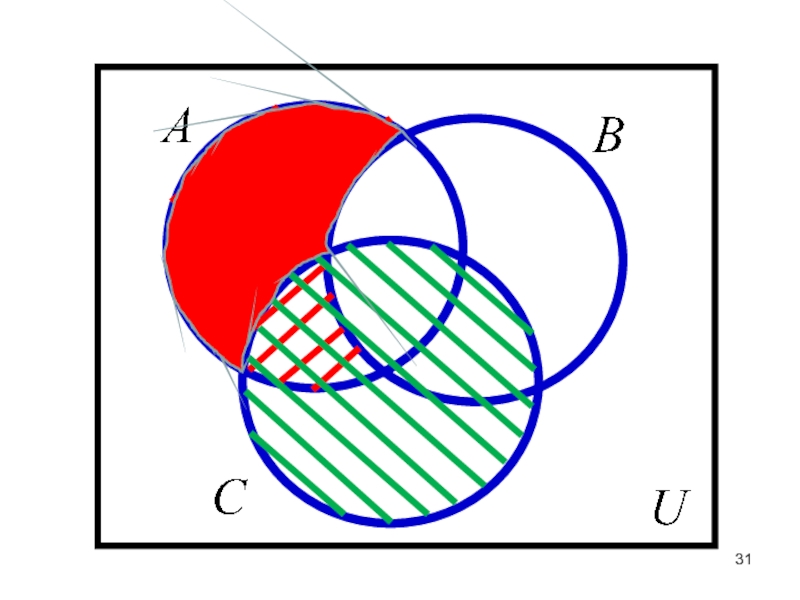
- 17. Объединением двух множеств А и В
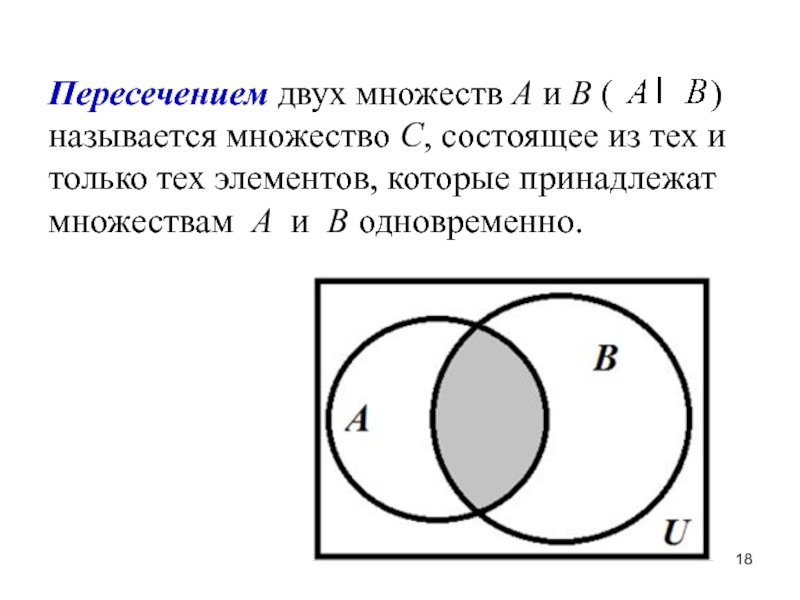
- 18. Пересечением двух множеств А и В (
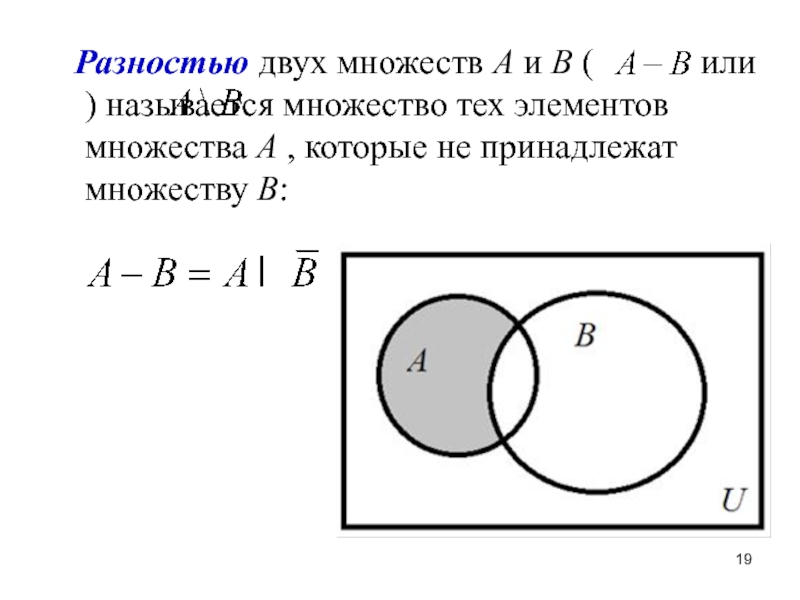
- 19. Разностью двух множеств А и В
- 20. Прямым (декартовым) произведением двух множеств
- 24. Пример 2 Прямое (декартово) произведение:
- 25. Пример 2 Из этого примера видно, что
- 34. Выучить или переписать в тетрадь определения на слайдах 2, 3, 6-8, 10, 12-20
Множество – это совокупность определенных различаемых объектов таких, что для любого объекта можно установить, принадлежит объект данному множеству или нет. Множество, которое подчиняется лишь такому ограничению, может содержать объекты почти
Слайд 2 Множество – это совокупность определенных различаемых объектов таких, что для
любого объекта можно установить, принадлежит объект данному множеству или нет.
Множество, которое подчиняется лишь такому ограничению, может содержать объекты почти любой природы.
Множество, которое подчиняется лишь такому ограничению, может содержать объекты почти любой природы.
Слайд 4Например:
- множество всех станций Московского метро;
- множество левых ботинок;
- множество натуральных чисел: 1, 2,
3, 4 и т. д.;
- множество символов, доступных специальному печатающему устройству;
- множество кодов операций конкретного компьютера.
- множество символов, доступных специальному печатающему устройству;
- множество кодов операций конкретного компьютера.
Слайд 5множество всех натуральных чисел: 1, 2, 3, . . . Обозначим N. Часто
0 считают натуральным числом. Множество N с добавлением 0 обозначается .
- множество всех натуральных чисел, не превосходящих 100.
- множество всех решений уравнения
- множество всех натуральных чисел, не превосходящих 100.
- множество всех решений уравнения
Слайд 6 Множество обозначают заглавными буквами, а его элементы – прописными.
Говоря об определенном множестве, мы полагаем, что для каждого объекта имеется две возможности: элемент либо входит в множество , либо нет .
Мощность множества – количество его элементов.
Обозначение мощности: .
Мощность множества – количество его элементов.
Обозначение мощности: .
Слайд 7Множество, не содержащее элементов, называется пустым множеством и обозначается Ø.
В
зависимости от их мощности множества различают как конечные или бесконечные.
Конечные множества могут состоять из одного или нескольких элементов.
Конечные множества могут состоять из одного или нескольких элементов.
Слайд 8Способы задания множества:
Перечисление всех элементов множества (список), например, множество однозначных неотрицательных
чисел
Множества часто рассматриваются как “неупорядоченные совокупности элементов”, хотя иногда полезно подчеркнуть, что, например
Множества часто рассматриваются как “неупорядоченные совокупности элементов”, хотя иногда полезно подчеркнуть, что, например
Слайд 10Порождающая процедура
Описывает способ получения элементов множества из уже полученных элементов либо
других объектов. Тогда элементы множества - все объекты, которые могут быть получены (построены) с помощью такой процедуры.
Слайд 11Множество натуральных степеней двойки.
Порождающую процедуру зададим
рекуррентно:
Какое множество задается рекуррентной формулой:
Какое множество задается рекуррентной формулой:
Слайд 12Задание множества описанием его элементов (разрешающая процедура)
указание общего свойства, которым обладают
все элементы множества, например, множество четных натуральных чисел
или
или
Слайд 13Множество А называют подмножеством множества В (обозначается
), если каждый элемент множества А является также элементом множества В.
Слайд 14 Множества А и В называют равными (
), если каждый элемент множества А является одновременно элементом множества В и наоборот,
т.е. если и .
т.е. если и .
Слайд 15 Множество U называется универсальным множеством (множество всех подмножеств)
для некоторой системы множеств, если каждое множество этой системы является подмножеством U , т.е.
Слайд 16Дополнением множества называется
множество, состоящее из тех и только тех элементов универсального множества, которые не входят в множество А.
Слайд 17 Объединением двух множеств А и В (
) называется множество С, состоящее из тех элементов, которые принадлежат или множеству А, или В, или А и В одновременно.
Слайд 18Пересечением двух множеств А и В (
) называется множество С, состоящее из тех и только тех элементов, которые принадлежат множествам А и В одновременно.
Слайд 19 Разностью двух множеств А и В (
или ) называется множество тех элементов множества А , которые не принадлежат множеству В:
Слайд 20 Прямым (декартовым) произведением двух множеств А и В называется
множество, состоящее из упорядоченных пар элементов, в которых первый элемент принадлежит множеству А, а второй – множеству В.
Слайд 24Пример 2
Прямое (декартово) произведение:
= {(-2, 0); (-2, 2); (-2, 4); (-2, 5); (-1, 0); (-1, 2); (-1, 4); (-1, 5); (0, 0); (0, 2); (0, 4); (0, 5); (1, 0); (1, 2); (1, 4); (1, 5); (2, 0); (2, 2); (2, 4); (2, 5)}
= {(0, -2); (0, -1); (0, 0); (0, 1); (0, 2); (2, -2); (2, -1); (2, 0); (2, 1); (2, 2); (4, -2); (4, -1); (4, 0); (4, 1); (4, 2); (5, -2); (5, -1); (5, 0); (5, 1); (5, 2)}
= {(0, -2); (0, -1); (0, 0); (0, 1); (0, 2); (2, -2); (2, -1); (2, 0); (2, 1); (2, 2); (4, -2); (4, -1); (4, 0); (4, 1); (4, 2); (5, -2); (5, -1); (5, 0); (5, 1); (5, 2)}
