фигуру, ограниченную со всех сторон плоскими многоугольниками.
Вершины многоугольников являются вершинами многогранника.
Стороны многоугольников образуют ребра.
Плоскости многоугольников – грани многогранника.
Сечением многогранника плоскостью является плоский многоугольник, вершины которого принадлежат ребрам, а стороны – граням многогранника.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Многогранники. Призма презентация
Содержание
- 1. Многогранники. Призма
- 2. Призма Призма – многогранник, две грани которого
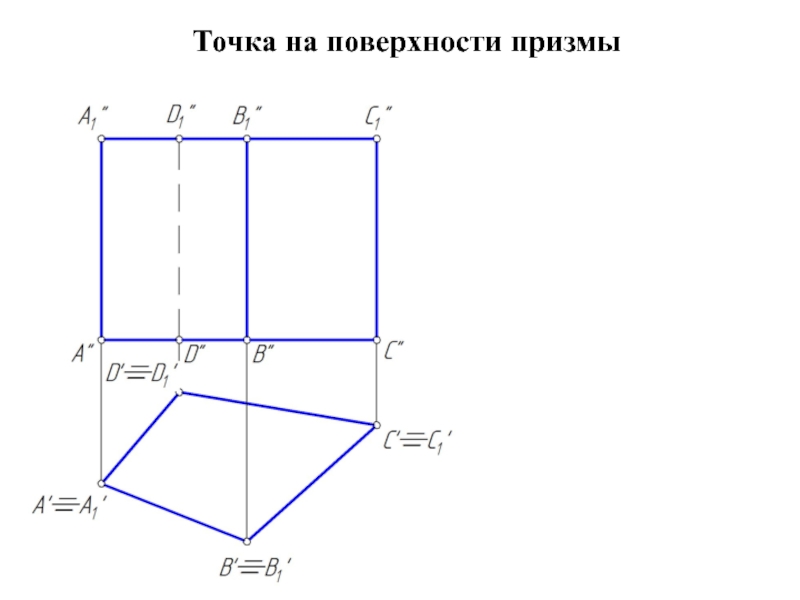
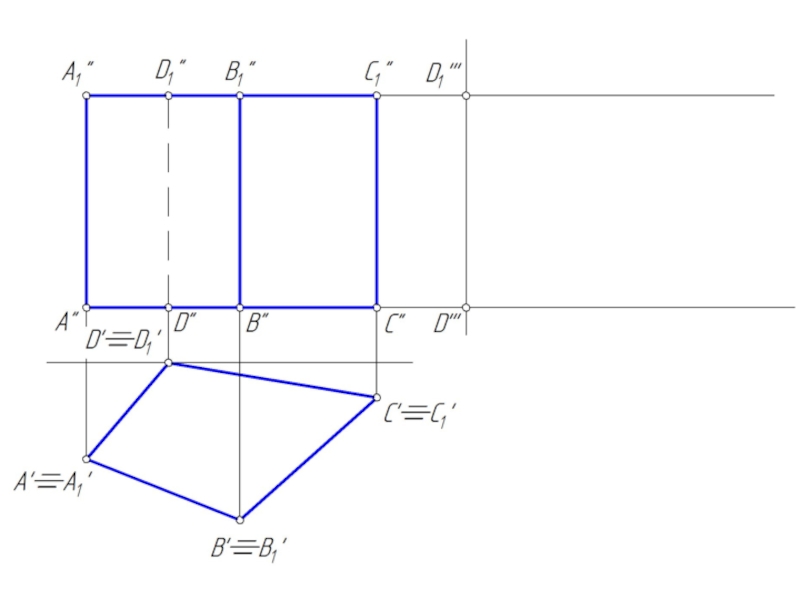
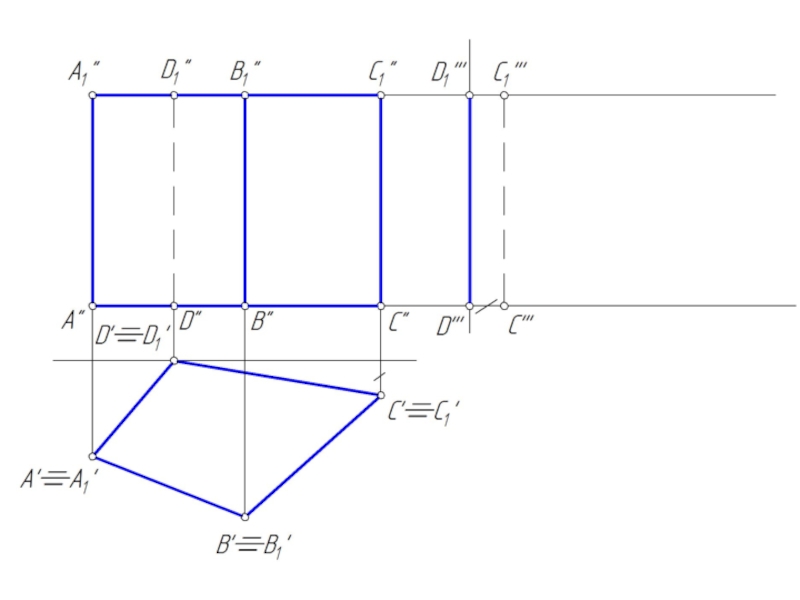
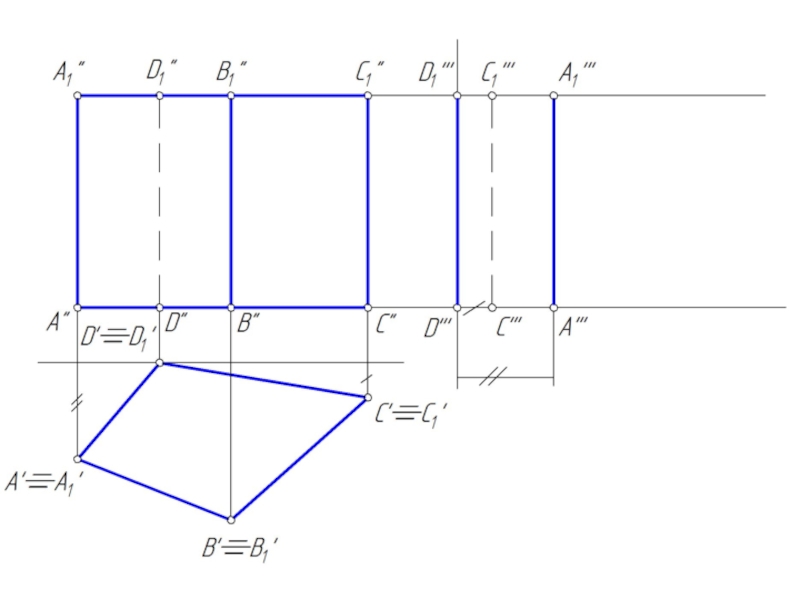
- 3. Точка на поверхности призмы
- 10. Пересечение призмы плоскостью При пересечении призмы плоскостью
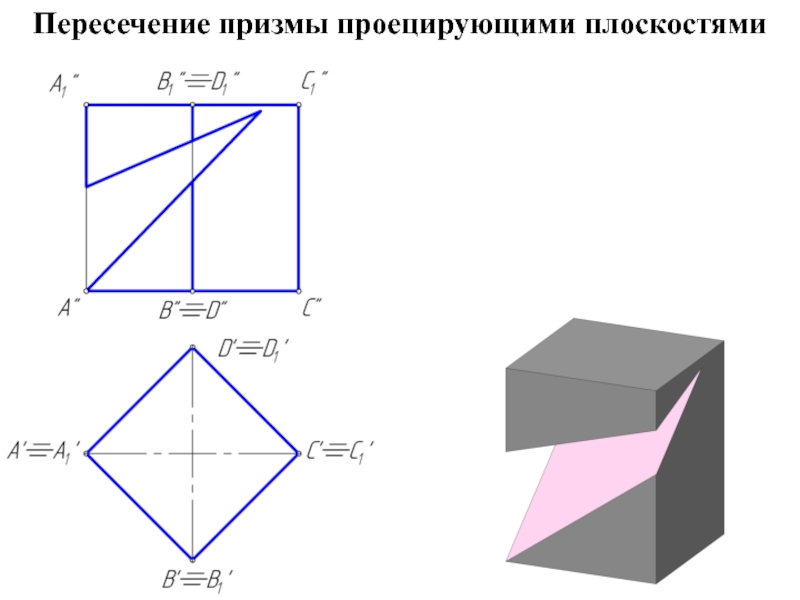
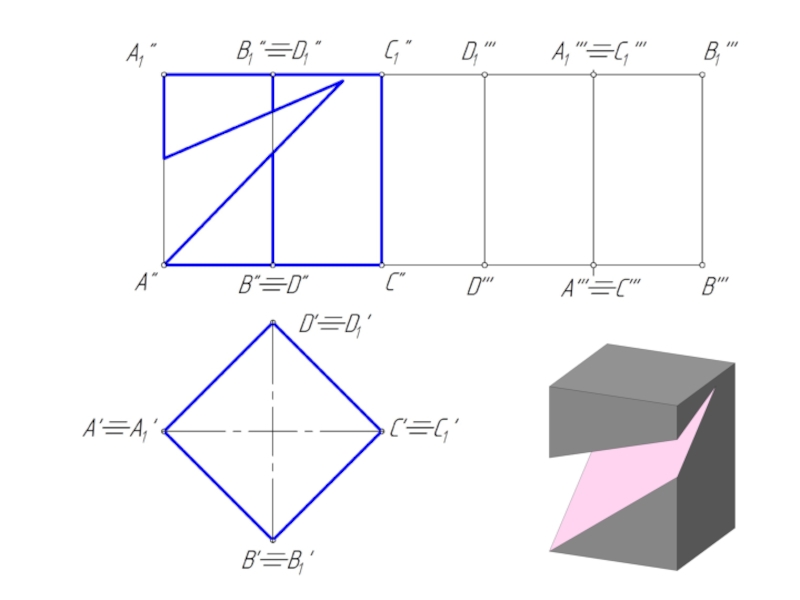
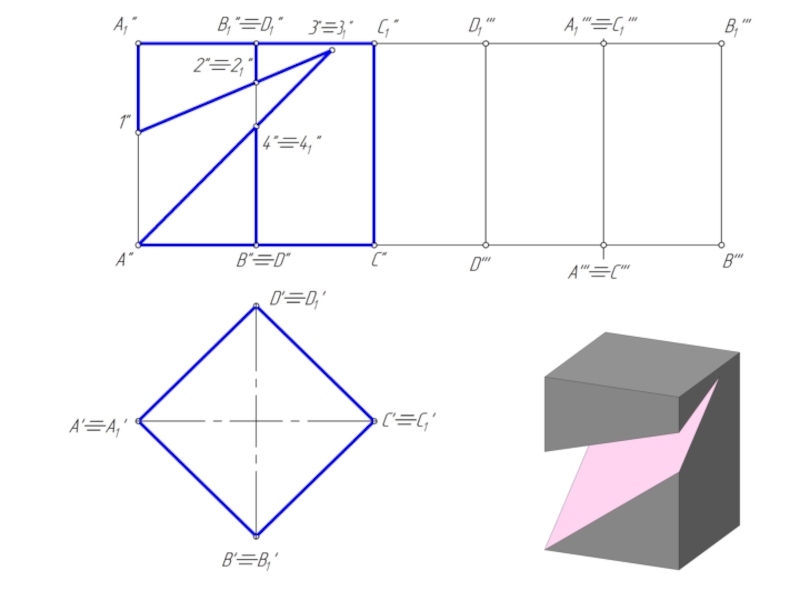
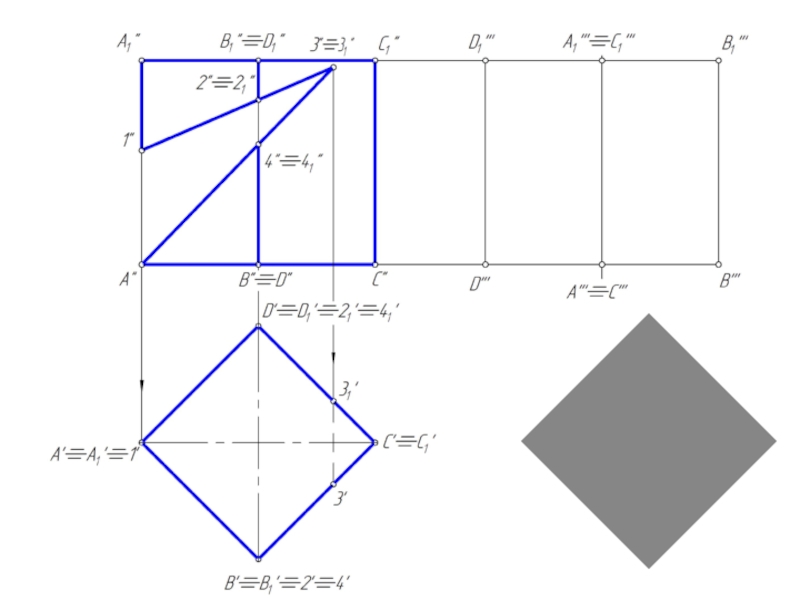
- 11. Пересечение призмы проецирующими плоскостями
- 18. Пересечение призмы прямой линией Построение точки пересечения
- 19. Построить точки пересечение прямой с призмой
Слайд 1Многогранники
Поверхность, образованная частями пересекающихся плоскостей – гранями, называется многогранной.
Многогранником называют пространственную
Слайд 2Призма
Призма – многогранник, две грани которого являются конгруэнтными (равными) многоугольниками, лежащими
в параллельных плоскостях, а остальные грани – параллелограммами (прямоугольниками), имеющими общие стороны с этими многоугольниками.
Прямая призма – боковые ребра перпендикулярны основанию.
Наклонная призма – боковые ребра расположены под произвольным углом к основанию.
Правильная призма – в основании призмы лежит правильный многоугольник, а боковые ребра перпендикулярны плоскостям основания.
Прямая призма – боковые ребра перпендикулярны основанию.
Наклонная призма – боковые ребра расположены под произвольным углом к основанию.
Правильная призма – в основании призмы лежит правильный многоугольник, а боковые ребра перпендикулярны плоскостям основания.
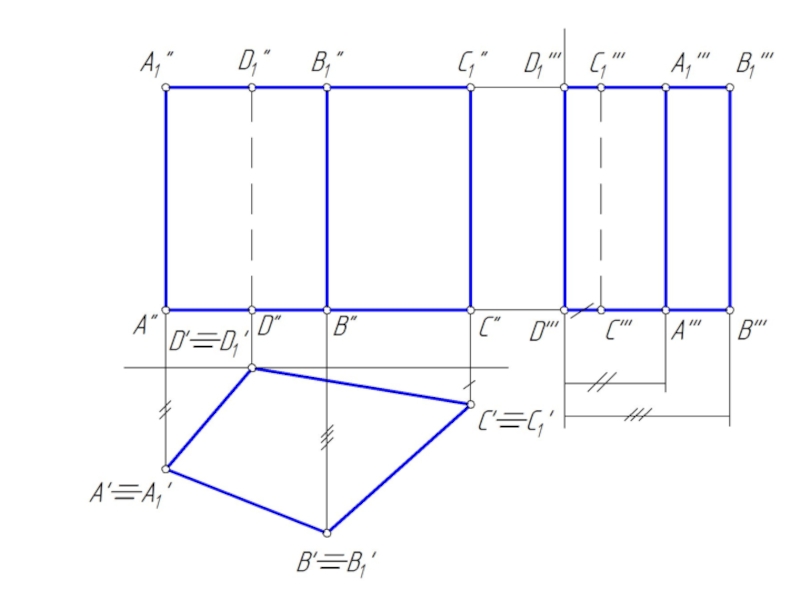
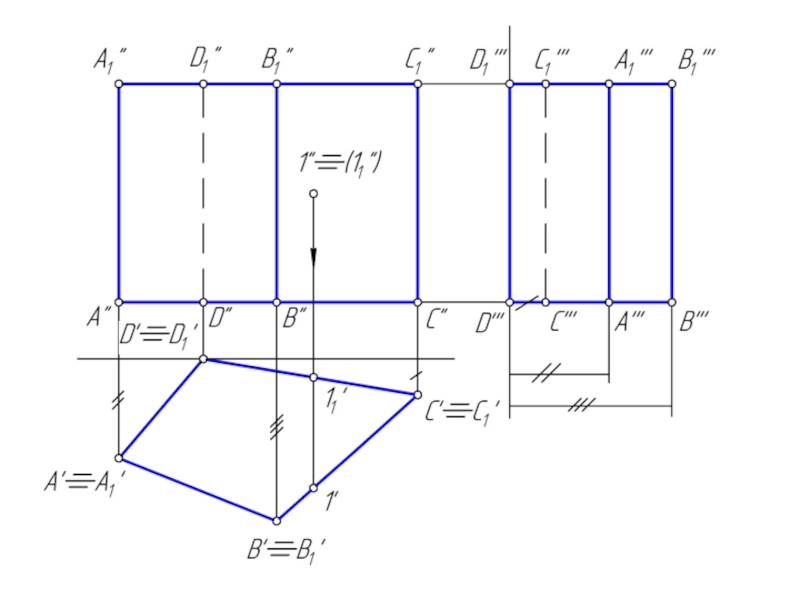
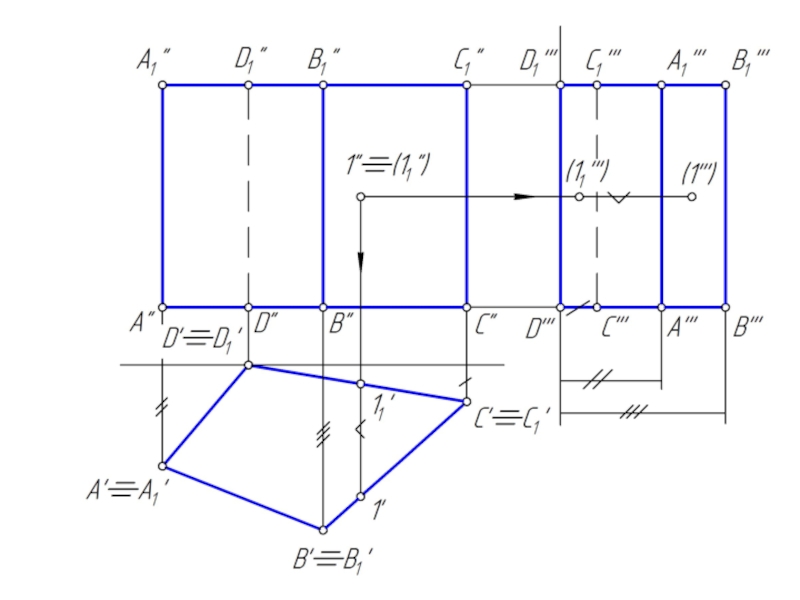
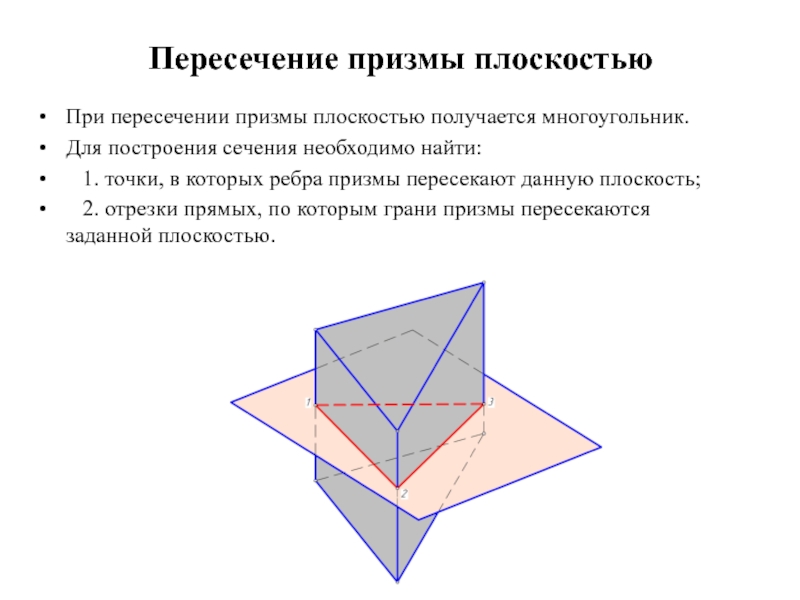
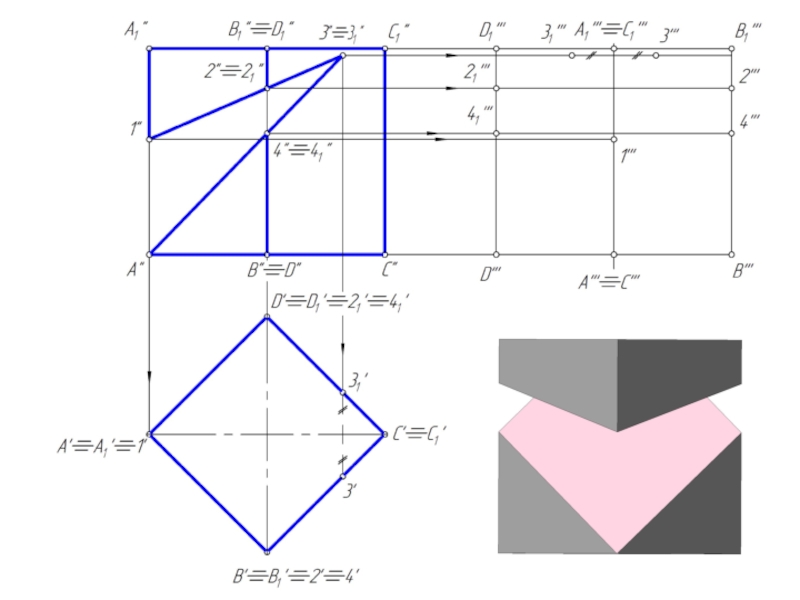
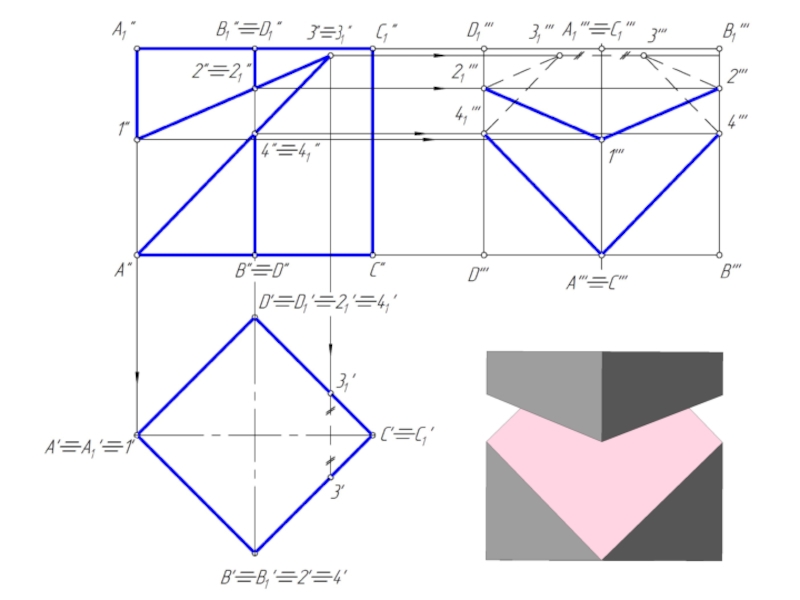
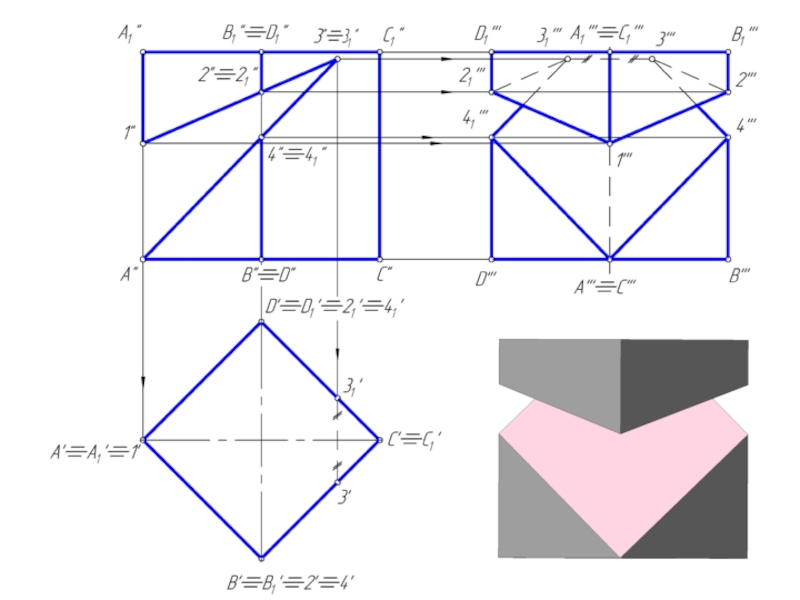
Слайд 10Пересечение призмы плоскостью
При пересечении призмы плоскостью получается многоугольник.
Для построения сечения необходимо
найти:
1. точки, в которых ребра призмы пересекают данную плоскость;
2. отрезки прямых, по которым грани призмы пересекаются заданной плоскостью.
1. точки, в которых ребра призмы пересекают данную плоскость;
2. отрезки прямых, по которым грани призмы пересекаются заданной плоскостью.
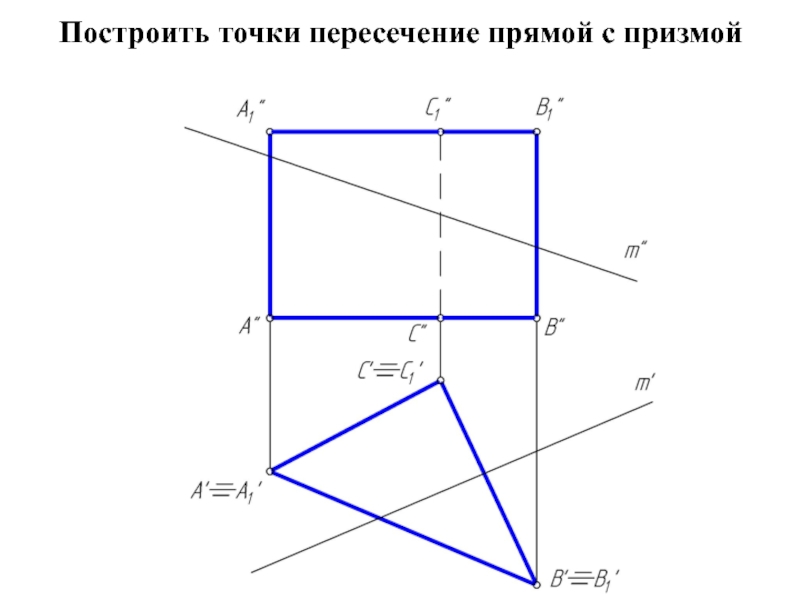
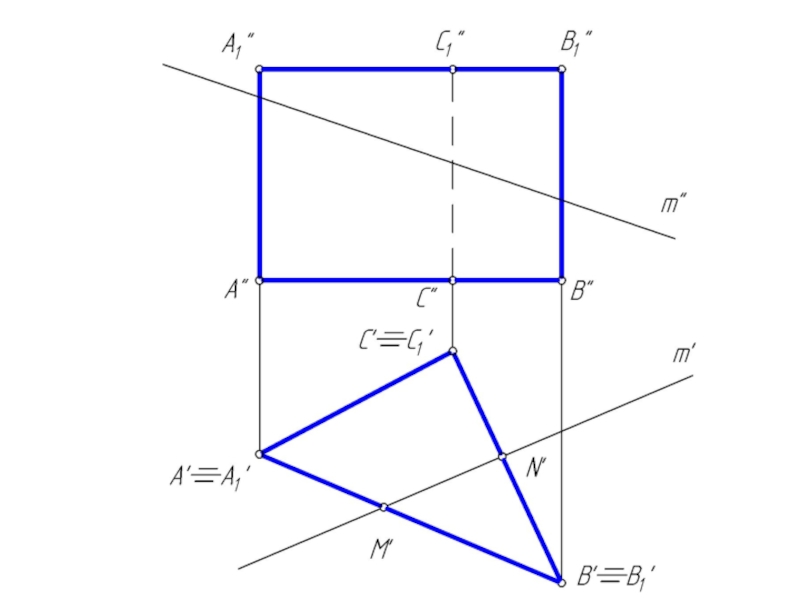
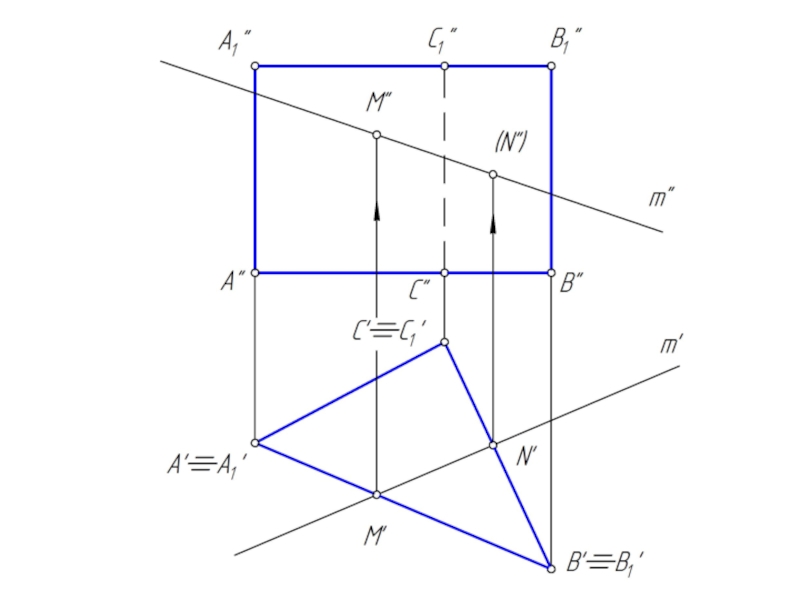
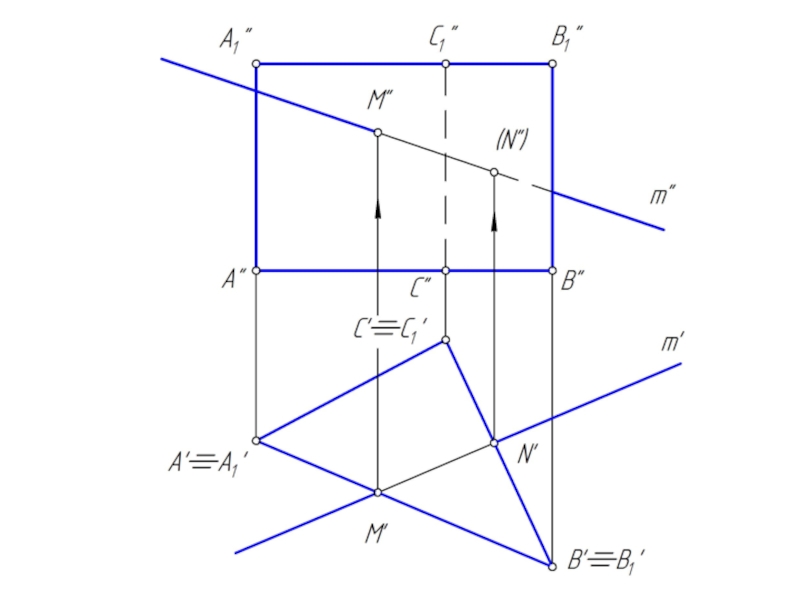
Слайд 18Пересечение призмы прямой линией
Построение точки пересечения прямой линии с призмой значительно
упрощается, если призма прямая и основание призмы параллельно плоскости проекции.
В этом случае боковые грани призмы занимают проецирующее положение в пространстве.
Исходя из свойства проецирующих плоскостей, проекции точек пересечения прямой с поверхностью призмы принадлежат проецирующему следу плоскости (боковой грани призмы).
В этом случае боковые грани призмы занимают проецирующее положение в пространстве.
Исходя из свойства проецирующих плоскостей, проекции точек пересечения прямой с поверхностью призмы принадлежат проецирующему следу плоскости (боковой грани призмы).