- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Мир правильных многогранников презентация
Содержание
- 1. Мир правильных многогранников
- 2. Мир правильных многогранников.
- 3. Математика владеет не только истиной, но и
- 4. ПРАВИЛЬНЫЙ МНОГОГРАННИК- выпуклый
- 5. «эдра» - грань «тетра» -
- 6. Тетраэдр – представитель правильных выпуклых многогранников. Поверхность
- 7. Куб или гексаэдр – представитель правильных выпуклых
- 8. Октаэдр – представитель семейства правильных выпуклых многогранников.
- 9. Додекаэдр – представитель семейства правильных выпуклых многогранников.
- 10. Икосаэдр – представитель семейства правильных выпуклых многогранников.
- 11. Модель Солнечной системы Кеплера.
- 12. «Космический кубок» И. Кеплера
- 14. Икосаэдро- додекаэдровая структура Земли.
- 15. Теорема Эйлера Число вершин
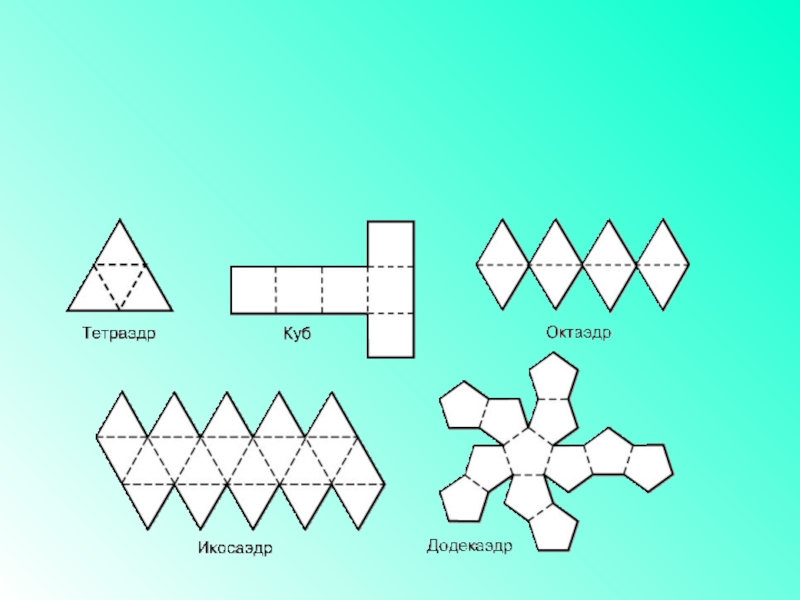
- 17. РАЗВЁРТКИ. 4-5 группы
- 18. Архимедовыми телами называются полуправильные однородные выпуклые многогранники,
- 19. Тела Архимеда.
- 20. Французский математик Пуансо в 1810 году построил
- 21. Малый звездчатый додекаэдр Большой звездчатый додекаэдр Большой икосаэдр Большой додекаэдр
- 22. Правильных многогранников вызывающе мало, но этот весьма
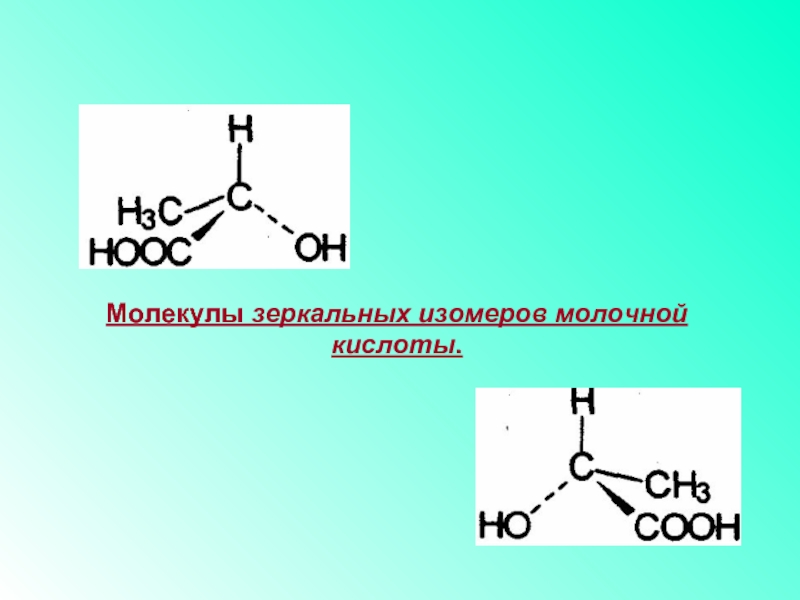
- 23. Химия.
- 24. Молекулы зеркальных изомеров молочной кислоты.
- 25. Кристаллы поваренной соли.
- 26. Биология.
- 27. Вирус полиомиелита имеет форму додекаэдра.
- 28. Украшения.
- 29. Правильная форма алмаза.
Мир правильных
многогранников.
Слайд 3Математика владеет не только истиной, но и высшей красотой - красотой
отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства.
Бертран Рассел
Бертран Рассел
Слайд 4
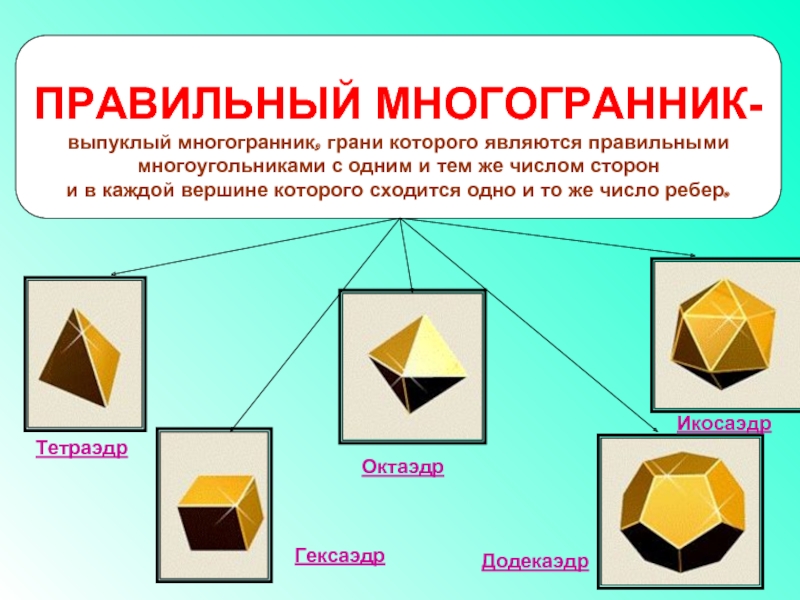
ПРАВИЛЬНЫЙ МНОГОГРАННИК-
выпуклый многогранник, грани которого являются правильными
многоугольниками с одним и
тем же числом сторон
и в каждой вершине которого сходится одно и то же число ребер.
и в каждой вершине которого сходится одно и то же число ребер.
Гексаэдр
Тетраэдр
Октаэдр
Додекаэдр
Икосаэдр
Слайд 6Тетраэдр – представитель правильных выпуклых многогранников.
Поверхность тетраэдра состоит из четырех равносторонних
треугольников, сходящихся в каждой вершине по три.
ТЕТРАЭДР
Слайд 7Куб или гексаэдр – представитель правильных выпуклых многогранников.
Куб имеет шесть квадратных
граней, сходящихся в каждой вершине по три.
КУБ (ГЕКСАЭДР)
Слайд 8Октаэдр – представитель семейства правильных выпуклых многогранников.
Октаэдр имеет восемь треугольных граней,
сходящихся в каждой вершине по четыре.
ОКТАЭДР
Слайд 9Додекаэдр – представитель
семейства правильных выпуклых многогранников.
Додекаэдр имеет двенадцать пятиугольных граней, сходящихся
в вершинах по три.
ДОДЕКАЭДР
Слайд 10Икосаэдр – представитель семейства правильных выпуклых многогранников.
Поверхность икосаэдра состоит из двадцати
равносторонних треугольников, сходящихся в каждой вершине по пять.
ИКОСАЭДР
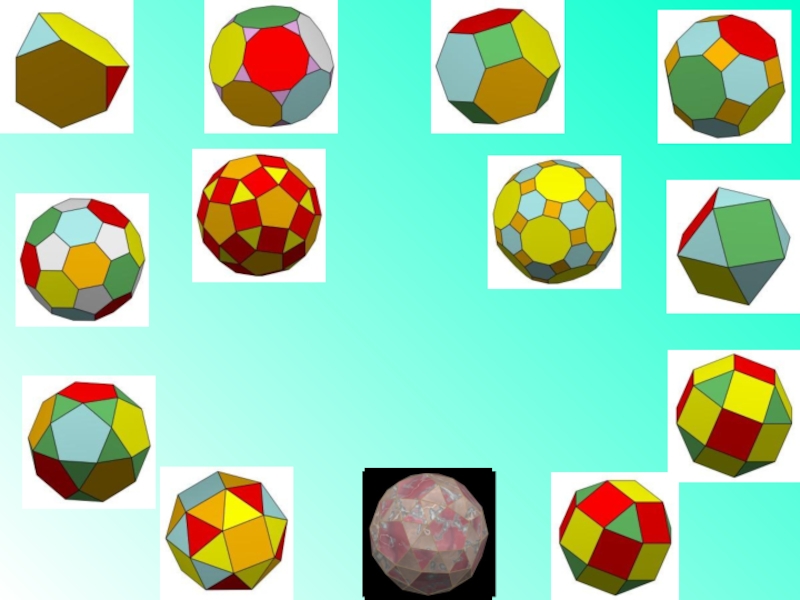
Слайд 18Архимедовыми телами называются полуправильные однородные выпуклые многогранники, то есть выпуклые многогранники,
все многогранные углы которых равны, а грани - правильные многоугольники нескольких типов.
Тела Архимеда.
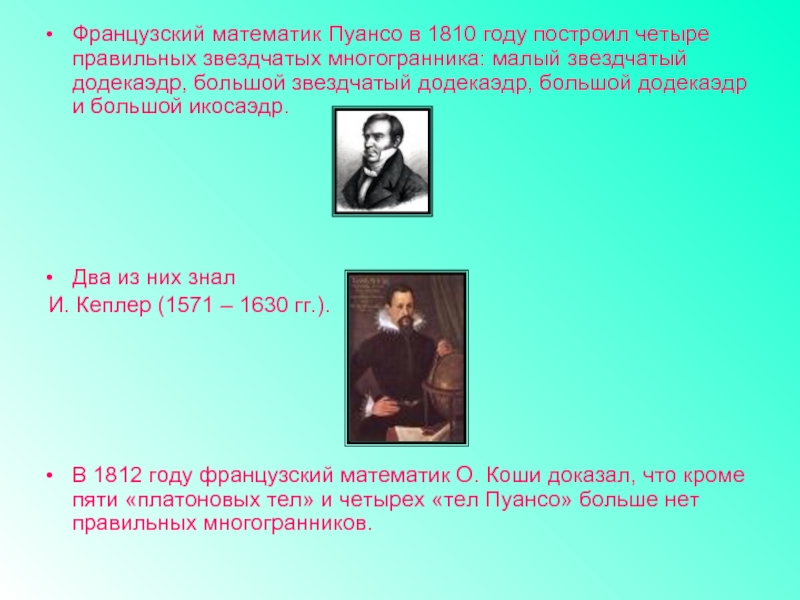
Слайд 20Французский математик Пуансо в 1810 году построил четыре правильных звездчатых многогранника:
малый звездчатый додекаэдр, большой звездчатый додекаэдр, большой додекаэдр и большой икосаэдр.
Два из них знал
И. Кеплер (1571 – 1630 гг.).
В 1812 году французский математик О. Коши доказал, что кроме пяти «платоновых тел» и четырех «тел Пуансо» больше нет правильных многогранников.
Два из них знал
И. Кеплер (1571 – 1630 гг.).
В 1812 году французский математик О. Коши доказал, что кроме пяти «платоновых тел» и четырех «тел Пуансо» больше нет правильных многогранников.
Слайд 22Правильных многогранников вызывающе мало, но этот весьма ск ромный по численности
отряд сумел пробраться в самые глубины различных наук.
Л. Кэррол
Л. Кэррол
