- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Методы решения показательных уравнений презентация
Содержание
- 1. Методы решения показательных уравнений
- 2. Первый метод решения – уравнивание оснований степеней
- 3. Решить уравнение Решение
- 4. Второй метод решения – вынесение общего
- 5. Решить уравнение Решение
- 6. Третий метод-вынесение за скобки общего множителя в
- 7. Решить уравнение Решение:
- 8. Четвертый метод – введение новой переменной
- 9. Решить уравнение Решение: Обозначим Уравнение примет вид:
- 10. Пятый метод – введение новой переменной в
- 11. Решить уравнение: Решение: Разделим обе части уравнения на Получим
- 12. Шестой метод – использование свойства монотонности функций
- 13. Решить уравнение Решение: Рассмотрим две функции.
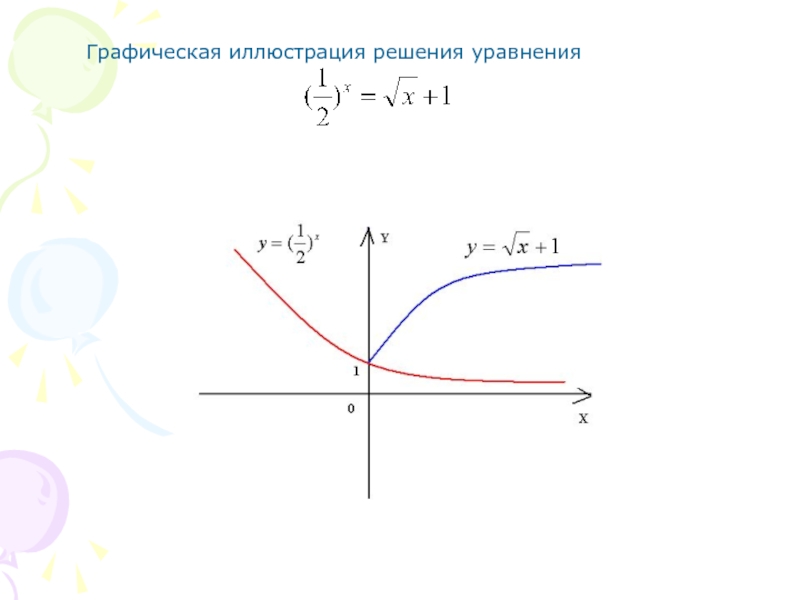
- 14. Графическая иллюстрация решения уравнения
- 16. Решить уравнение Решение: Прологарифмируем обе части
- 17. Презентацию подготовила учитель математики БГОУ СОШ №531 Красногвардейского района города Санкт-Петербурга СМИРНОВА Галина Васильевна
Слайд 2Первый метод решения – уравнивание оснований степеней
Суть данного метода заключается в
используя свойства степеней,
мы приводим уравнение к виду
это уравнение равносильно уравнению
При решении используем определения и свойства степеней
Слайд 4Второй метод решения – вынесение
общего множителя за скобки
Суть метода заключается
свойства степеней, выносим за скобки степень
с наименьшим показателем
При решении используем свойство степеней
Слайд 6Третий метод-вынесение за скобки общего
множителя в уравнениях, содержащих
степени с разными
Суть метода заключается в следующем:
1.Переносим слагаемые с разными основаниями
в разные стороны уравнения
2.В левой и правой части уравнения выносим
за скобку степени с наименьшими показателями
3.Делим обе части уравнения на подходящие множители,
чтобы получить уравнение вида
Слайд 8Четвертый метод – введение новой переменной
Обозначим
Уравнение примет вид
Решая квадратное уравнение
По свойствам показательной функции
- положительно
Для положительных значений решаем уравнение
Слайд 10Пятый метод – введение новой переменной
в однородных показательных уравнениях
Данный метод применяется
Обозначим
Уравнение примет вид
По свойствам показательной функции
- положительно
Разделим обе части уравнения на
Уравнение примет вид
Решаем квадратное уравнение и для положительных
значений t решаем уравнение
Слайд 12Шестой метод – использование свойства монотонности
функций
Теорема: Пусть функция
возрастает на
а функция
убывает на этом же промежутке.
Тогда уравнение
имеет на этом промежутке
не более одного корня.
Суть метода в следующем:
1.Определяем монотонность функций в левой и правой
частях уравнения
2.Угадываем корень уравнения
3.На основании теоремы делаем вывод
о единственности найденного корня
Слайд 13Решить уравнение
Решение: Рассмотрим две функции.
функция, убывающая на всей
функция возрастающая на всей числовой оси
является очевидным корнем уравнения.
По теореме этот корень – единственный