- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Методы решения дифференциальных уравнений в частных производных презентация
Содержание
- 1. Методы решения дифференциальных уравнений в частных производных
- 2. Дифференциальное уравнение в частных производных Системы ДУЧП
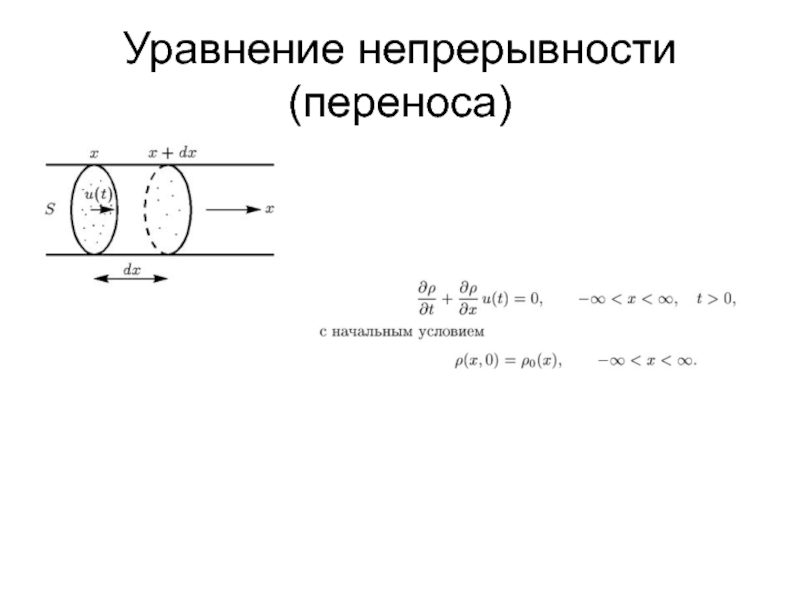
- 3. Уравнение непрерывности (переноса)
- 4. Уравнение непрерывности (переноса)
- 5. Уравнение переноса
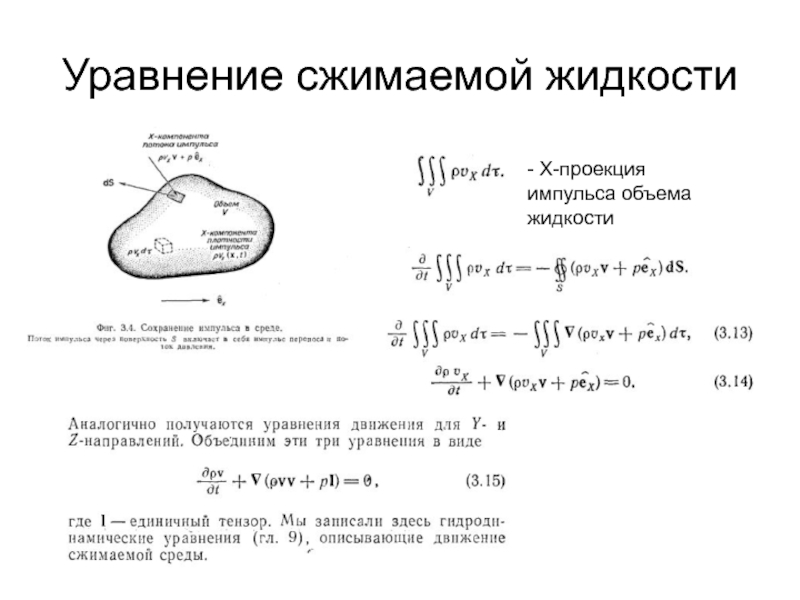
- 6. Уравнение сжимаемой жидкости - Х-проекция импульса объема жидкости
- 7. Уравнения классической гидродинамики уравнение состояния
- 8. Уравнение теплопроводности
- 9. Уравнения электромагнетизма
- 10. Консервативные ДУ
- 11. Уравнение диффузии
- 12. Волновое уравнение
- 13. Уравнение Пуассона и Лапласа
- 14. Классификация ДУЧП 2-го порядка
- 15. Аппроксимация производных конечными разностями
- 16. Граничные и начальные условия
- 17. Аппроксимация производных конечными разностями
- 18. Аппроксимация 1-го порядка точности
- 19. Аппроксимация 1-го порядка точности
- 20. Центральная аппроксимация 2-го порядка
- 21. Центральная аппроксимация 2-ой производной
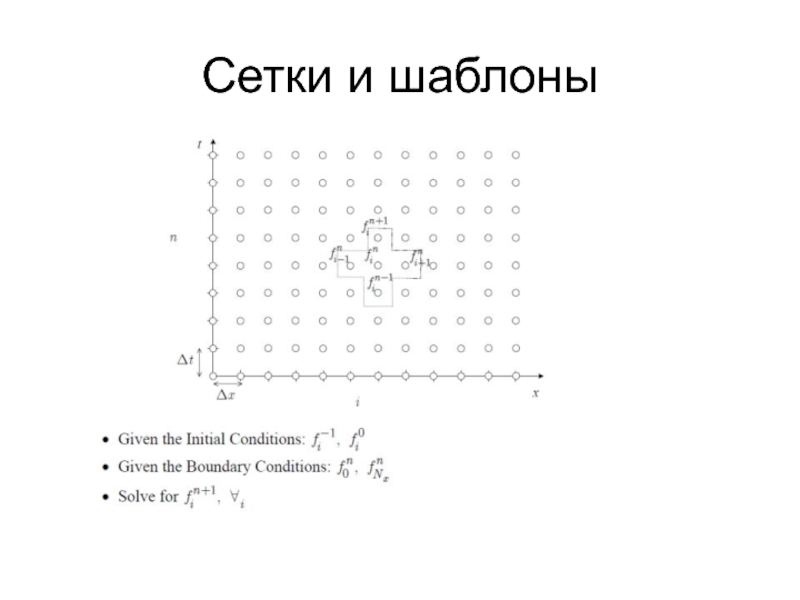
- 22. Сетки и шаблоны
- 23. Точность аппроксимации
- 24. Явные и неявные схемы
- 25. Методы составления схем Метод разностной аппроксимации Интегро-интерполяционный метод (законы сохранения) Метод неопределенных коэффициентов
- 26. Сходимость
- 27. Анализ устойчивости по методу Неймана Исследуется
- 28. Анализ устойчивости Матрица перехода может меняться по
- 29. Анализ уравнения переноса
- 31. Схема Лакса
- 32. Дисперсия и диффузия на сетке Разностная схема
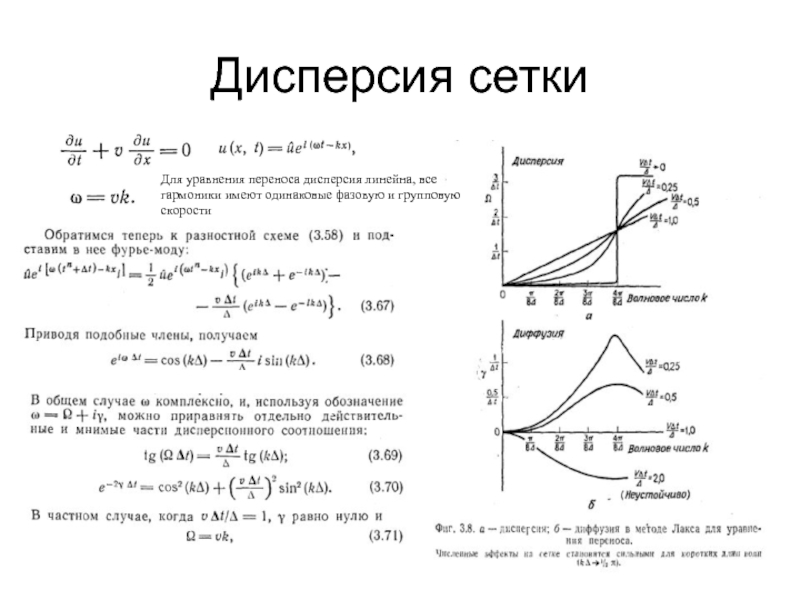
- 33. Дисперсия сетки Для уравнения переноса дисперсия линейна, все гармоники имеют одинаковые фазовую и групповую скорости
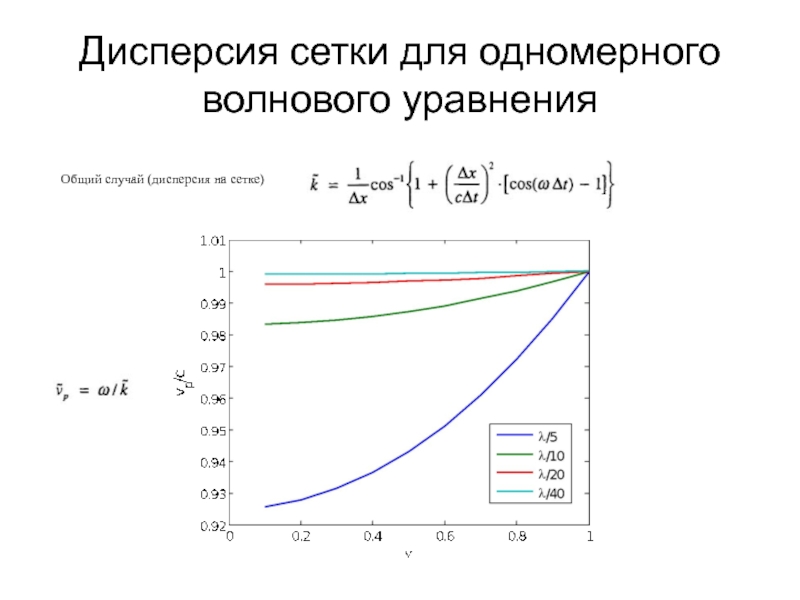
- 34. Дисперсия сетки для одномерного волнового уравнения Теперь рассмотрим дисперсию схемы
- 35. Дисперсия сетки для одномерного волнового уравнения Рассмотрим случай очень плотной сетки Рассмотрим случай
- 36. Дисперсия сетки для одномерного волнового уравнения Общий случай (дисперсия на сетке)
- 37. Схема 2-го порядка точности по времени и пространству (Лакса-Вендрофа)
- 38. Схема 2-го порядка точности по времени и пространству (Лакса-Вендрофа)
- 39. Устойчивость метода Лакса-Вендрофа
- 40. Диффузия в схеме Лакса-Вендрофа
- 41. Условие устойчивости в многомерных задачах гиперболического типа Метод Лакса
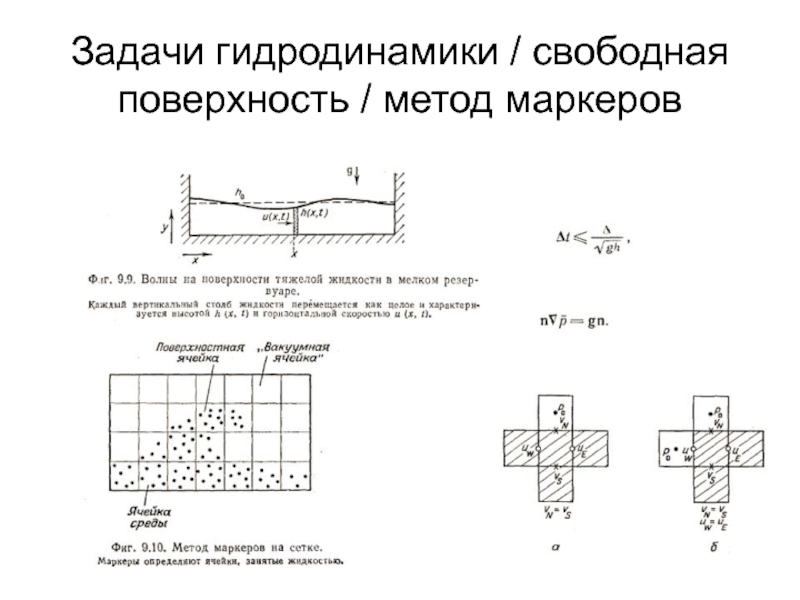
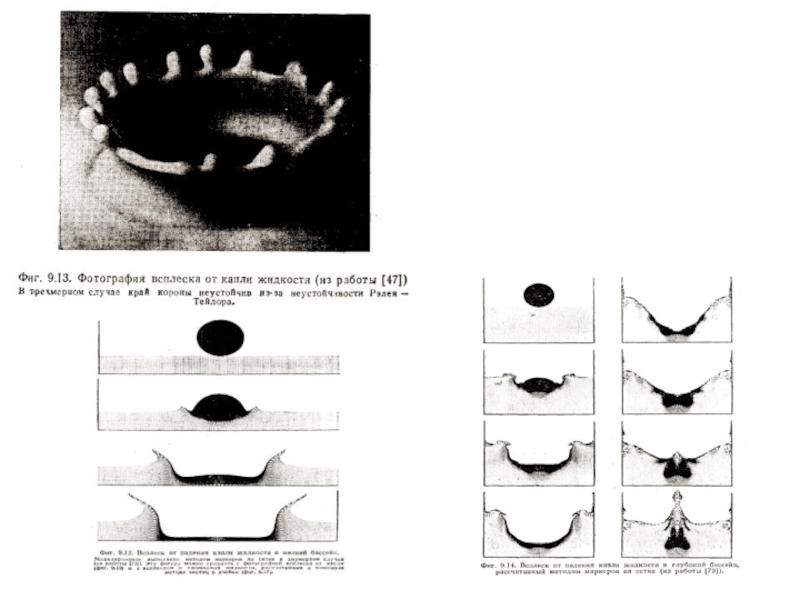
- 42. Задачи гидродинамики / свободная поверхность / метод маркеров
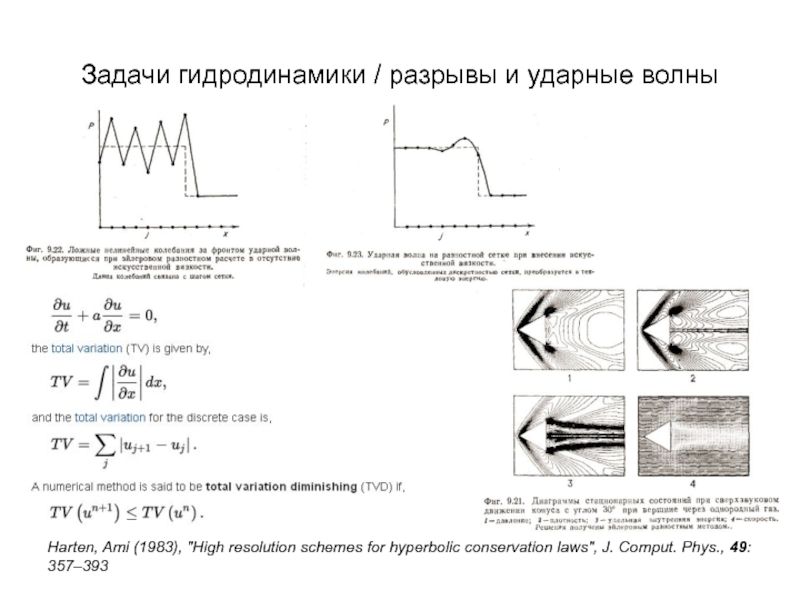
- 45. Задачи гидродинамики / разрывы и ударные волны
- 46. Консервативные схемы
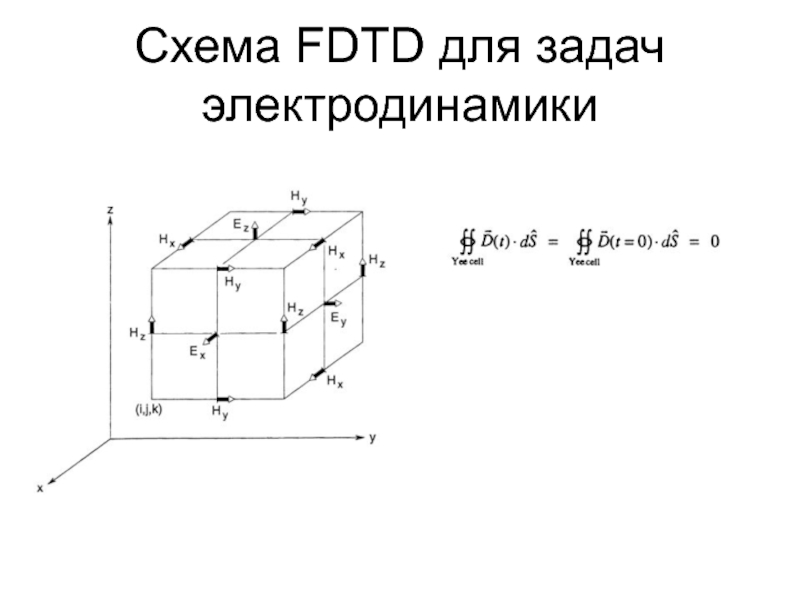
- 47. Схема FDTD для задач электродинамики
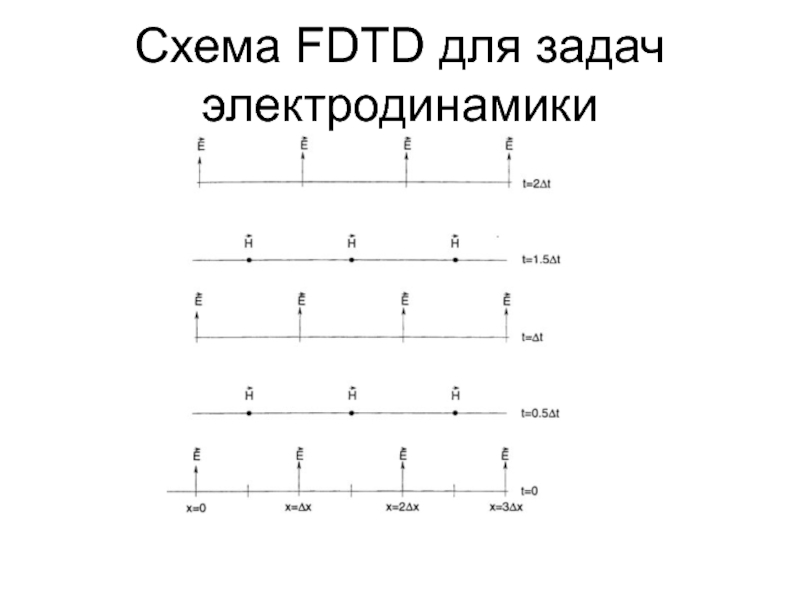
- 48. Схема FDTD для задач электродинамики
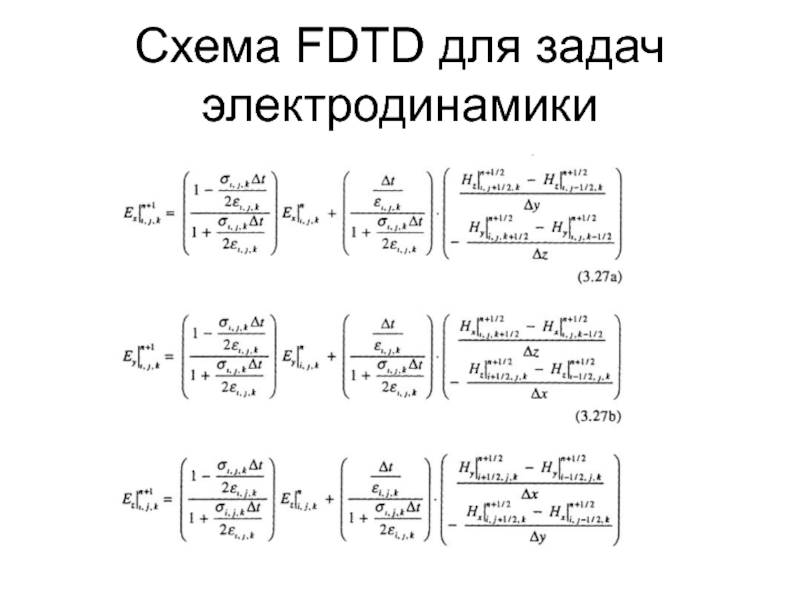
- 49. Схема FDTD для задач электродинамики
- 50. Схема FDTD для задач электродинамики
- 51. Схема FDTD для задач электродинамики
- 52. Схема FDTD для задач электродинамики
- 53. Схема FDTD для задач электродинамики
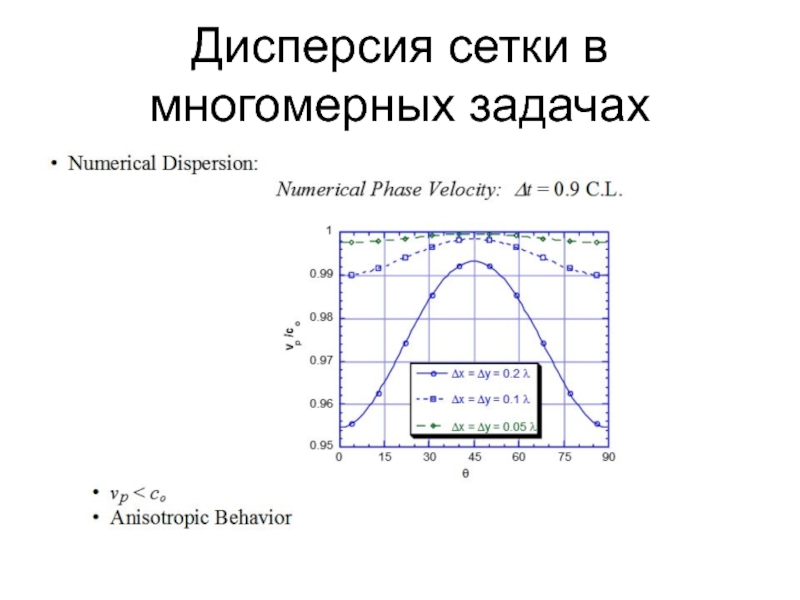
- 54. Дисперсия сетки в многомерных задачах
- 55. Устойчивость Computational Electrodynamics: The Finite-Difference Time-Domain
Дифференциальное уравнение в частных производных Системы ДУЧП
Слайд 25Методы составления схем
Метод разностной аппроксимации
Интегро-интерполяционный метод (законы сохранения)
Метод неопределенных коэффициентов
Слайд 27Анализ устойчивости по методу Неймана
Исследуется поведение Фурье-мод на сетке независимо
друг от друга. Требуется устойчивость для каждой из мод в отдельности.
G – матрица перехода разностной схемы для выбранной фурье-моды с волновым числом k.
Устойчивость моды предполагает, что если ее амплитуда в начальный момент времени конечна, то она должна оставаться конечной на всех n шагах.
Разложим моду по собственным векторам G
Тогда
и условие устойчивости -
Слайд 28Анализ устойчивости
Матрица перехода может меняться по пространственной и временной сеткам –
условие устойчивости должно выполняться глобально.
Слайд 32Дисперсия и диффузия на сетке
Разностная схема Лакса соответствует ДУ с диффузионным
членом (3), который компенсирует нестабильность, связанную с тем, что схема не центрирована по времени.
Слайд 33Дисперсия сетки
Для уравнения переноса дисперсия линейна, все гармоники имеют одинаковые фазовую
и групповую скорости
Слайд 35Дисперсия сетки для одномерного волнового уравнения
Рассмотрим случай очень плотной сетки
Рассмотрим случай
Слайд 45Задачи гидродинамики / разрывы и ударные волны
Harten, Ami (1983), "High resolution
schemes for hyperbolic conservation laws", J. Comput. Phys., 49: 357–393
Слайд 55Устойчивость
Computational Electrodynamics: The Finite-Difference Time-Domain Method, Third Edition
Allen Taflove
