- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Метод площадей. Теория презентация
Содержание
- 1. Метод площадей. Теория
- 2. Метод площадей. Теория. Теорема 1.
- 3. Метод площадей. Теория. Теорема
- 4. Метод площадей. Теория. Теорема 3.
- 5. Метод площадей. Теория.
- 6. Метод площадей. Теория. Теорема 5.
- 7. Метод площадей. Задачи-иллюстрации. В треугольнике
- 8. Метод площадей. Задачи-иллюстрации. Диагонали разделили четырехугольник
- 9. Метод площадей. Задачи-иллюстрации. А В С
- 10. Метод площадей. Задачи-иллюстрации. В трапеции проведены
- 11. Метод площадей. Задачи-иллюстрации. Площадь параллелограмма
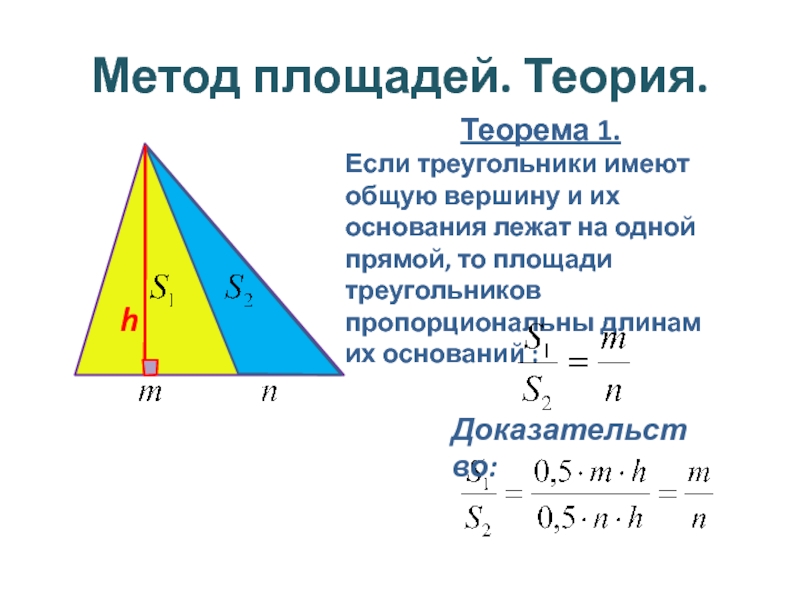
Слайд 2Метод площадей. Теория.
Теорема 1.
Если треугольники имеют общую вершину и их основания
h
Доказательство:
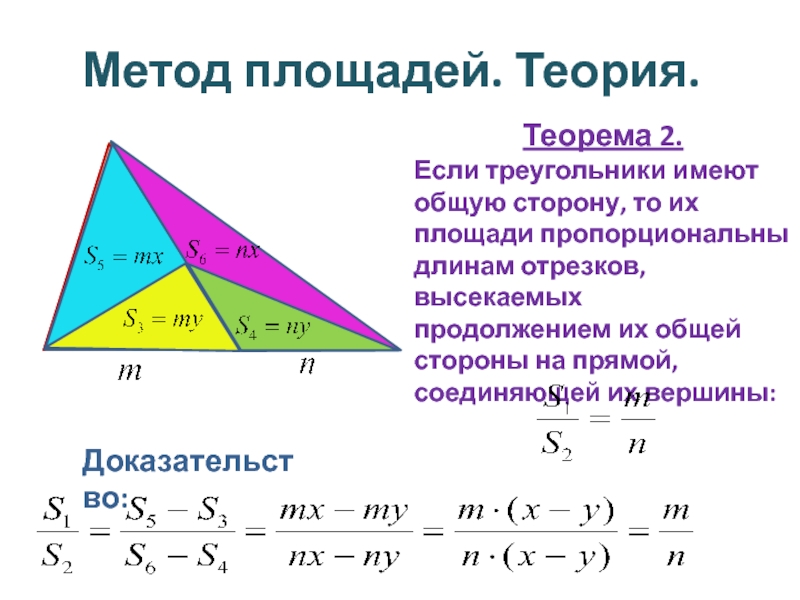
Слайд 3Метод площадей. Теория.
Теорема 2.
Если треугольники имеют общую сторону, то их площади
Доказательство:
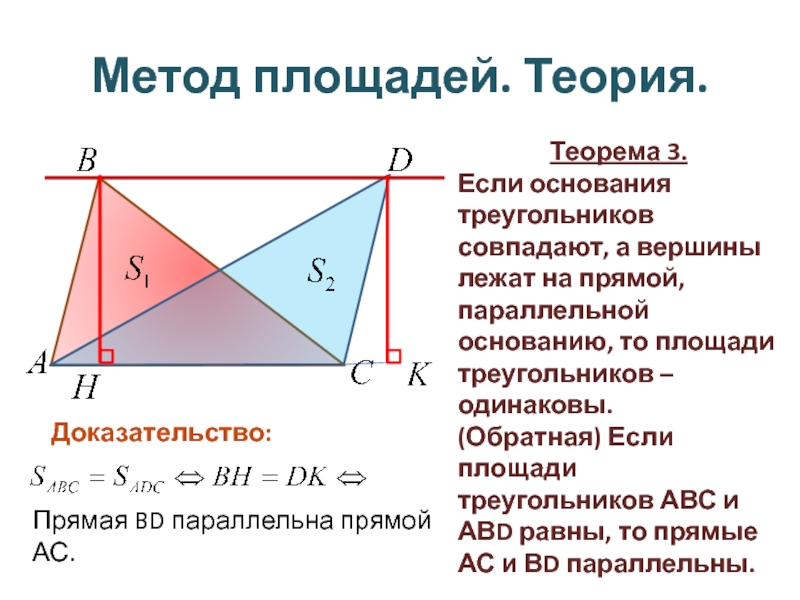
Слайд 4Метод площадей. Теория.
Теорема 3.
Если основания треугольников
совпадают, а вершины лежат на
(Обратная) Если площади треугольников АВС и АВD равны, то прямые АС и ВD параллельны.
Доказательство:
Прямая BD параллельна прямой АС.
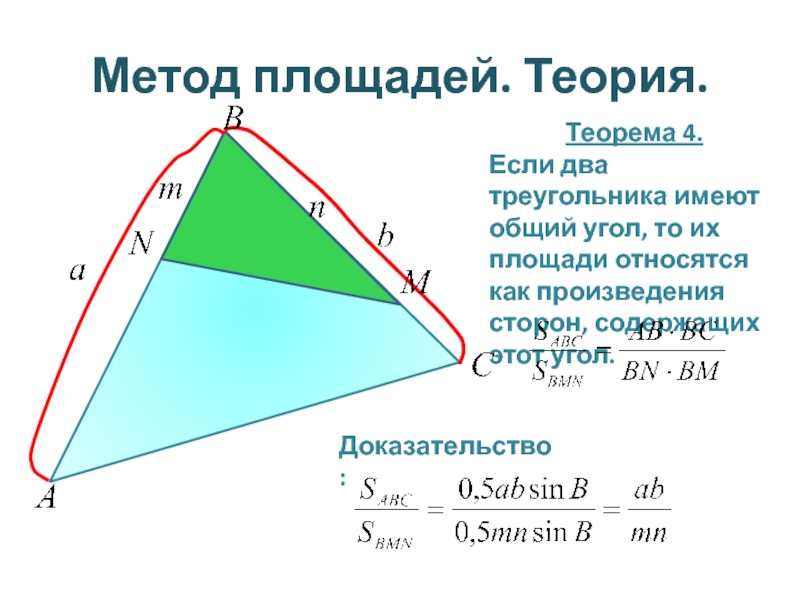
Слайд 5Метод площадей. Теория.
Теорема 4.
Если два треугольника имеют общий угол, то их
Доказательство:
Слайд 6Метод площадей. Теория.
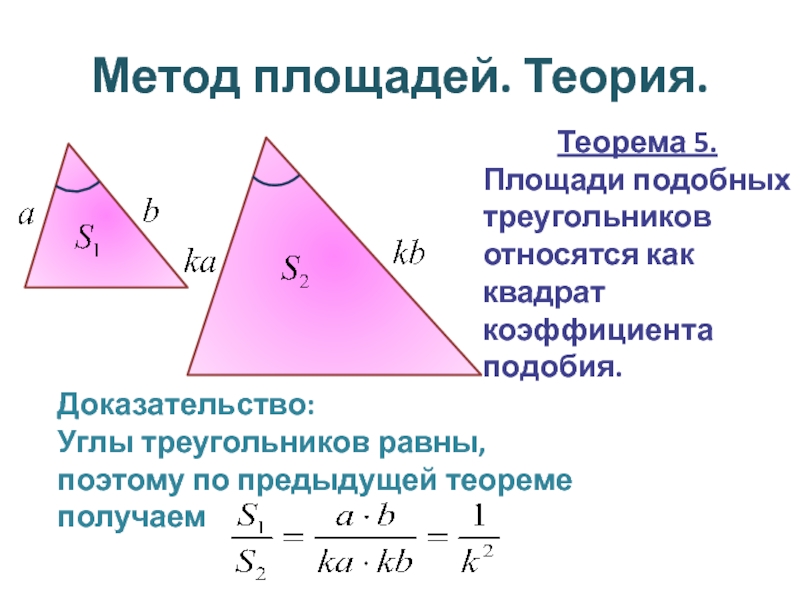
Теорема 5.
Площади подобных треугольников относятся как квадрат коэффициента подобия.
Доказательство:
Углы
Слайд 7Метод площадей.
Задачи-иллюстрации.
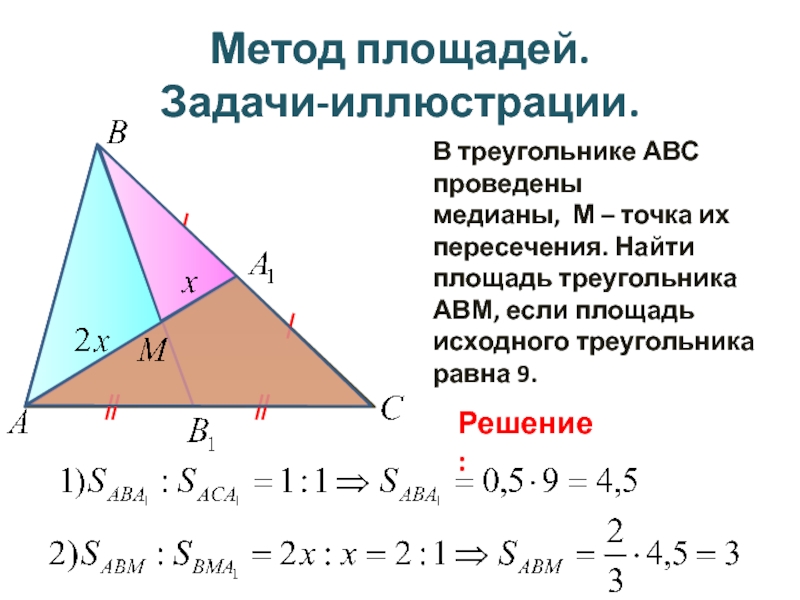
В треугольнике АВС проведены
медианы, М – точка их пересечения.
Решение:
Слайд 8Метод площадей.
Задачи-иллюстрации.
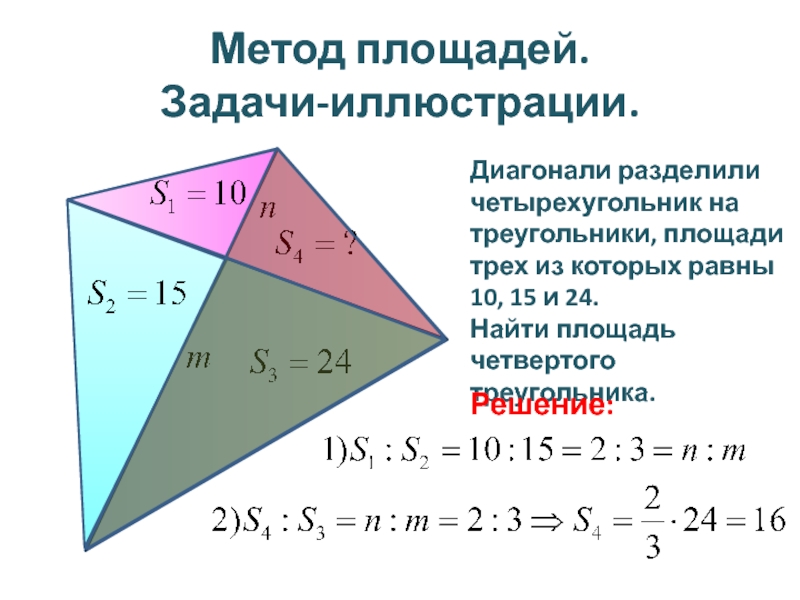
Диагонали разделили четырехугольник на треугольники, площади трех из которых равны
Найти площадь четвертого треугольника.
Решение:
Слайд 9Метод площадей.
Задачи-иллюстрации.
А
В
С
N
P
M
12
18
10
5
24
?
?
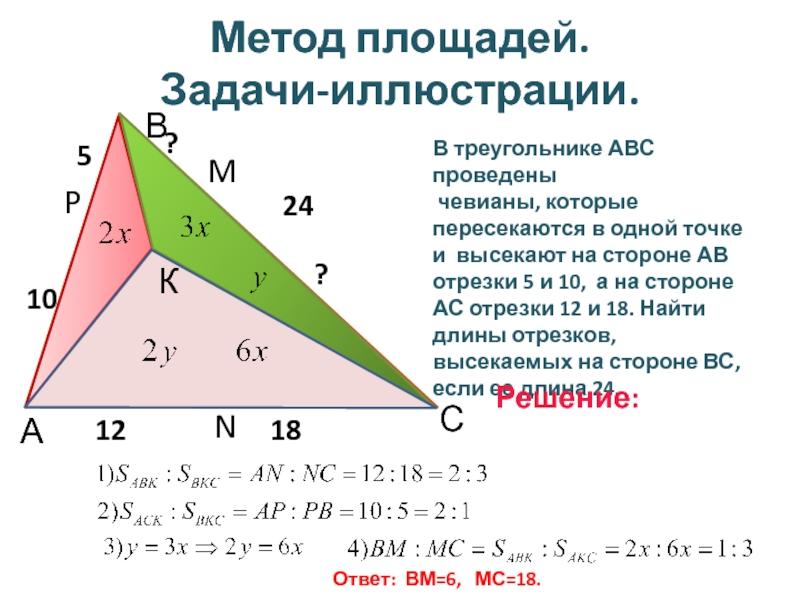
В треугольнике АВС проведены
чевианы, которые пересекаются в одной точке
Решение:
Ответ: ВМ=6, МС=18.
К
Слайд 10Метод площадей.
Задачи-иллюстрации.
В трапеции проведены обе
диагонали. Ее основания
относятся как 2:3.
трапеции равна 75. Найти площади ее кусочков.
Решение:
ΔАОD подобен ΔСОВ
с коэффициентом 2:3. Следовательно,
2) Площади треугольников ABD и
ACD одинаковы, треугольник AOD – их общая часть, поэтому площади
треугольников АОВ и СOD равны.
3) Используем отношение площадей:
Тогда
Таким образом,
Слайд 11Метод площадей.
Задачи-иллюстрации.
Площадь параллелограмма ABCD
равна 10. Найти площадь
четырехугольника MNPQ.
Решение:
1) Найдем площадь
2) Найдем площадь треугольника BPL:
3) Аналогично, площади треугольников ABN, ADM и CQD равны 2.
4) Тогда