- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Метод областей презентация
Содержание
- 1. Метод областей
- 2. Выдающийся французский математик, физик и писатель, один
- 3. «Предмет математики настолько серьёзен, что надо не
- 4. Гипотеза: можно ли ,очень удобный метод интервалов
- 5. ВВЕДЕНИЕ Для успешного исследования многих задач повышенной
- 6. Метод областей особенно полезен при решении уравнений
- 7. ЦЕЛИ РАБОТЫ: Рассмотреть «метод областей» как общий
- 8. Указать множество точек плоскости (х; у), удовлетворяющих
- 9. Заметим, что все прямые «порождены» сомножителями, входящими
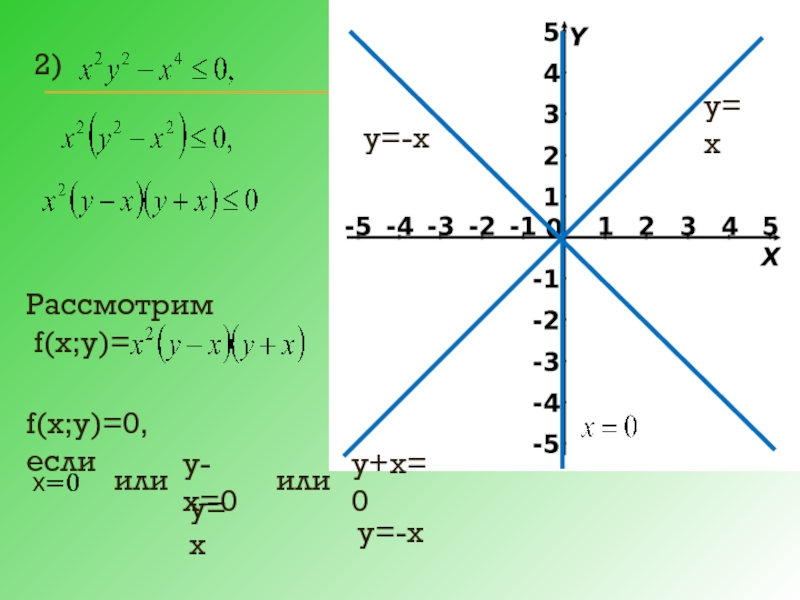
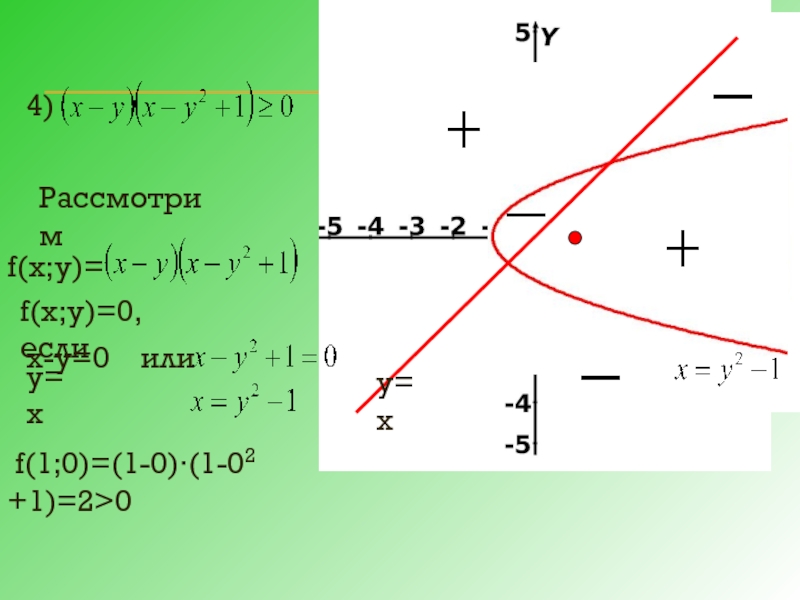
- 10. 2) Рассмотрим f(х;у)= f(х;у)=0, если или
- 11. у=х у=-х В отличии от примера 1
- 12. Преобразуем неравенство: Рассмотрим f(х;у)= f(х;у)=0, если у=0;
- 13. f(х;у)= f(х;у)=0, если х-у=0 или у=х f(1;0)=(1-0)∙(1-02 +1)=2>0 4) Рассмотрим у=х
- 14. Решение систем неравенств с параметром «Методом областей»
- 15. Найти наименьшее значение параметра а , при
- 16. б) Рассмотрим f(х;а)= f(х;у)=0, если f(1;0)= 12 -2∙1-1=-2
- 17. Найти наибольшее значение параметра а , при
- 18. б) Рассмотрим f(х;а)= f(х;у)=0, если f(0;0)=-2
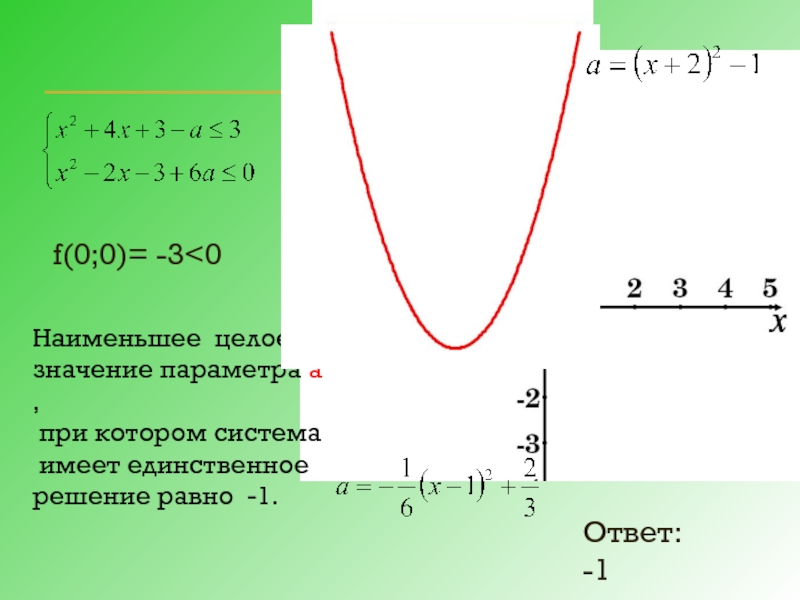
- 19. Найти наименьшее целое значение параметра
- 20. Преобразуем систему: 1) Рассмотрим f(х;а)= f(х;у)=0,
- 21. f(0;0)= 3>0
- 22. 2)Рассмотрим f(х;а)= f(х;у)=0, если Это квадратичная
- 23. f(0;0)= -3
- 24. Готовимся к ЕГЭ!
- 25. Найдите все значения а , при каждом
- 26. а) Рассмотрим f(х;а)= f(х;у)=0, если Это
- 27. б) Рассмотрим f(х;а)= f(х;у)=0, если Это
- 28. Система неравенств имеет решение, если
- 29. Действительно, точки (½;¼) и (³∕₂;¼) принадлежат
- 30. Метод областей можно назвать методом интервалов
- 31. Проверь себя!
- 32. Системы неравенств с параметрами
- 33. При каких значениях параметра «а» , система
- 34. Найти наименьшее целое значение параметра «а» ,при
- 35. Найти наибольшее целое значение параметра «а» ,при котором система имеет хотя бы одно решение:
- 36. Замечание: метод областей как таковой – лишь
- 37. Список использованной литературы. Математика для поступающих в
- 38. САФИНА АЛИНА
Выдающийся французский математик, физик и писатель, один из создателей математического анализа, проектной геометрии, теории вероятностей, гидростатики, создатель механического счетного устройства – «паскалева колеса» и наконец философ, чьи мысли оказывали влияние на
Слайд 1ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА
ПО ТЕМЕ
«Метод областей»
Работу выполнили:
Сафина Алина и Харламова Анастасия,
ученицы 10«а» класса МОУ «СОШ № 236 г.Знаменск»
Научный руководитель:
учитель математики Потапова Е.А.
Слайд 2Выдающийся французский математик, физик и писатель, один из создателей математического анализа,
проектной геометрии, теории вероятностей, гидростатики, создатель механического счетного устройства – «паскалева колеса» и наконец философ, чьи мысли оказывали влияние на многих выдающихся людей сказал:
Блэз Паскаль
Blaise Pascal
(19.06.1623 – 19.08.1662)
Слайд 3«Предмет математики настолько серьёзен, что надо не упускать случая сделать его
занимательным»
«Крупное научное открытие даёт решение крупной проблемы , но и в решении любой задачи присутствует крупица открытия»
Слайд 4Гипотеза:
можно ли ,очень удобный метод интервалов для решения рациональных неравенств, применить
при решении неравенств с параметрами?
Слайд 5ВВЕДЕНИЕ
Для успешного исследования многих задач повышенной сложности полезно уметь строить не
только графики функций, но и множества точек плоскости, координаты которых удовлетворяют заданным уравнениям, неравенствам или их системам. Эффективно строить на координатной плоскости такие множества позволяет метод областей. Это весьма полезный прием можно назвать обобщающим методом интервалов.
Слайд 6Метод областей особенно полезен при решении уравнений или неравенств с параметром.
Применение метода интервалов в таких случаях затруднено, так как взаимное расположение точек, отмечаемых на числовой оси, может изменяться в зависимости от значений параметра. Это означает необходимость сравнивать их между собой и рассматривать различные случаи. В этой ситуации нам может помочь метод областей.
Слайд 7ЦЕЛИ РАБОТЫ:
Рассмотреть «метод областей» как общий прием решения неравенств на плоскости;
Применить
«метод областей» к решению задач с параметрами.
Показать типы задач, которые могут быть решены с помощью данного метода.
Показать типы задач, которые могут быть решены с помощью данного метода.
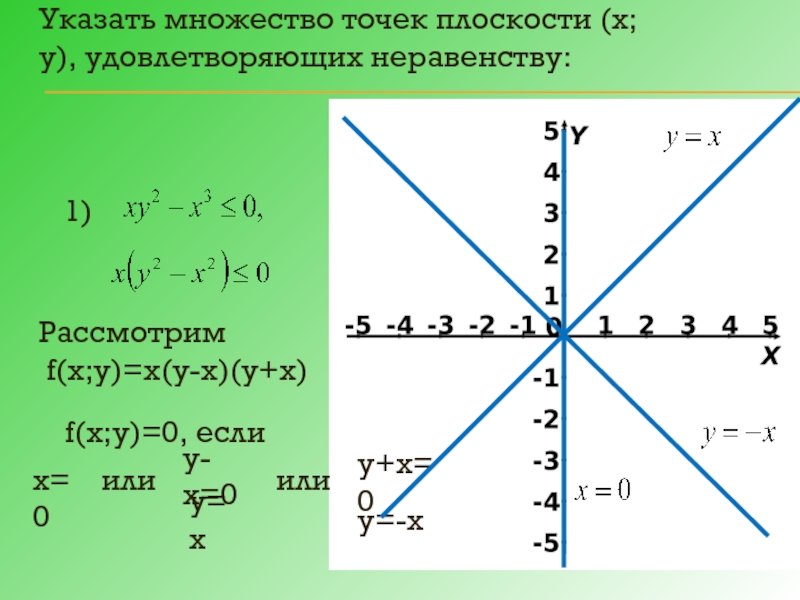
Слайд 8Указать множество точек плоскости (х; у), удовлетворяющих неравенству:
Рассмотрим
f(х;у)=х(у-х)(у+х)
f(х;у)=0,
если
у-х=0
у+х=0
или
у=х
у=-х
х=0
или
1)
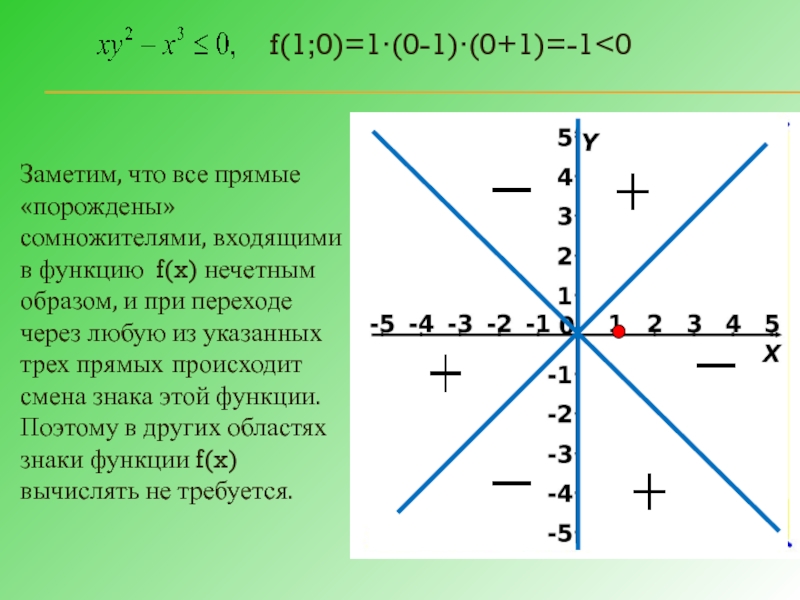
Слайд 9Заметим, что все прямые «порождены» сомножителями, входящими в функцию f(x) нечетным
образом, и при переходе через любую из указанных трех прямых происходит смена знака этой функции. Поэтому в других областях знаки функции f(x) вычислять не требуется.
f(1;0)=1∙(0-1)∙(0+1)=-1<0
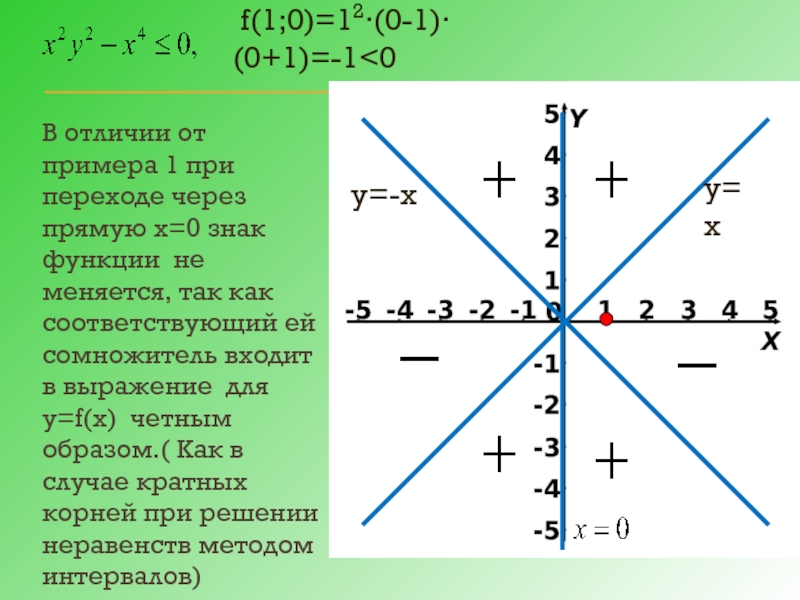
Слайд 11у=х
у=-х
В отличии от примера 1 при переходе через прямую х=0 знак
функции не меняется, так как соответствующий ей сомножитель входит в выражение для у=f(x) четным образом.( Как в случае кратных корней при решении неравенств методом интервалов)
f(1;0)=12∙(0-1)∙(0+1)=-1<0
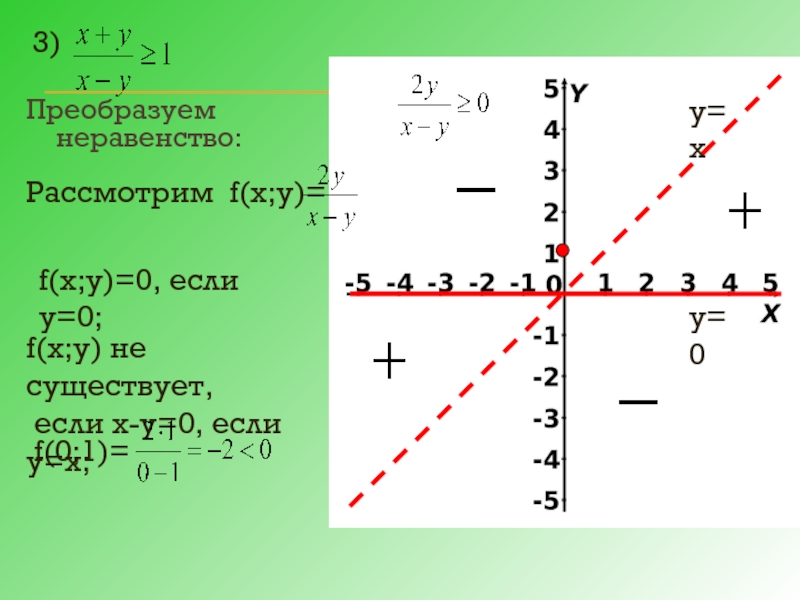
Слайд 12Преобразуем неравенство:
Рассмотрим f(х;у)=
f(х;у)=0, если у=0;
f(х;у) не существует,
если х-у=0, если у=х;
f(0;1)=
3)
у=х
у=0
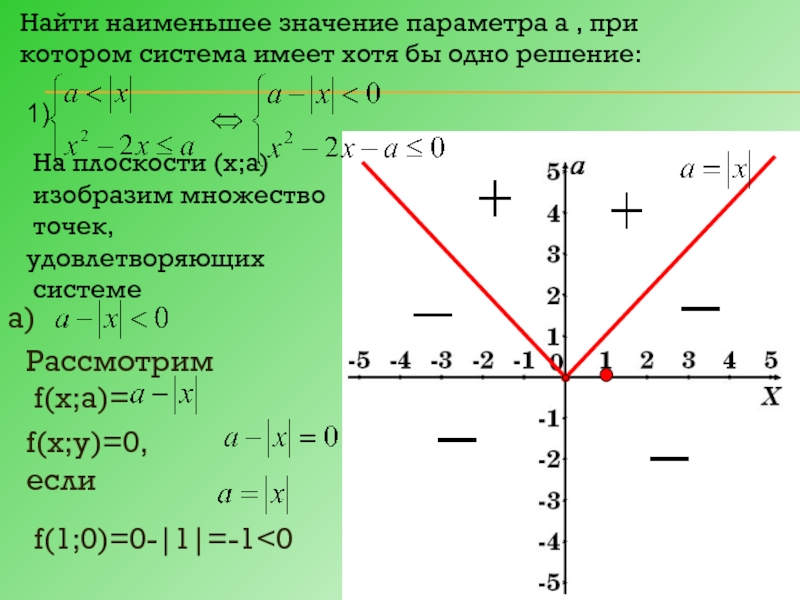
Слайд 15Найти наименьшее значение параметра а , при котором система имеет хотя
бы одно решение:
На плоскости (х;а)
изобразим множество
точек, удовлетворяющих
системе
а)
Рассмотрим
f(х;а)=
f(х;у)=0, если
f(1;0)=0-|1|=-1<0
1)
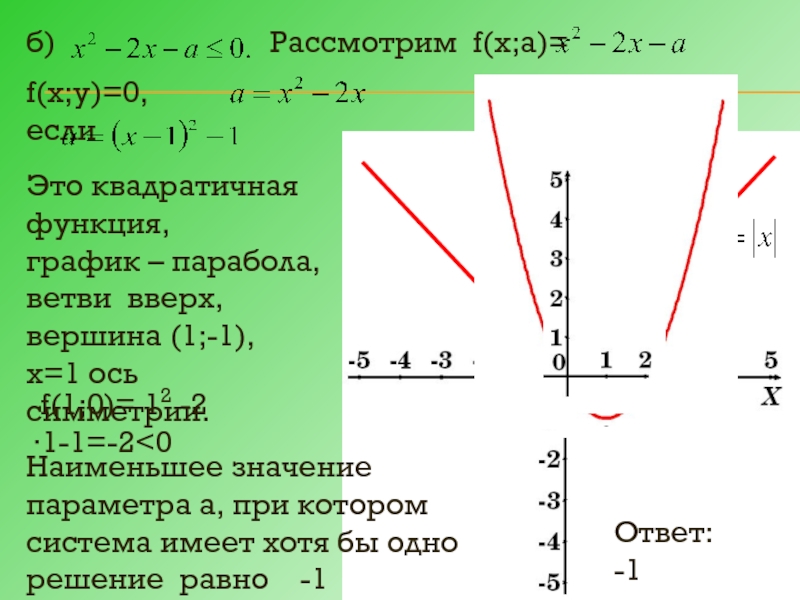
Слайд 16
б)
Рассмотрим f(х;а)=
f(х;у)=0, если
f(1;0)= 12 -2∙1-1=-2
вверх,
вершина (1;-1),
х=1 ось симметрии.
х=1 ось симметрии.
Наименьшее значение параметра а, при котором система имеет хотя бы одно решение равно -1
Ответ: -1
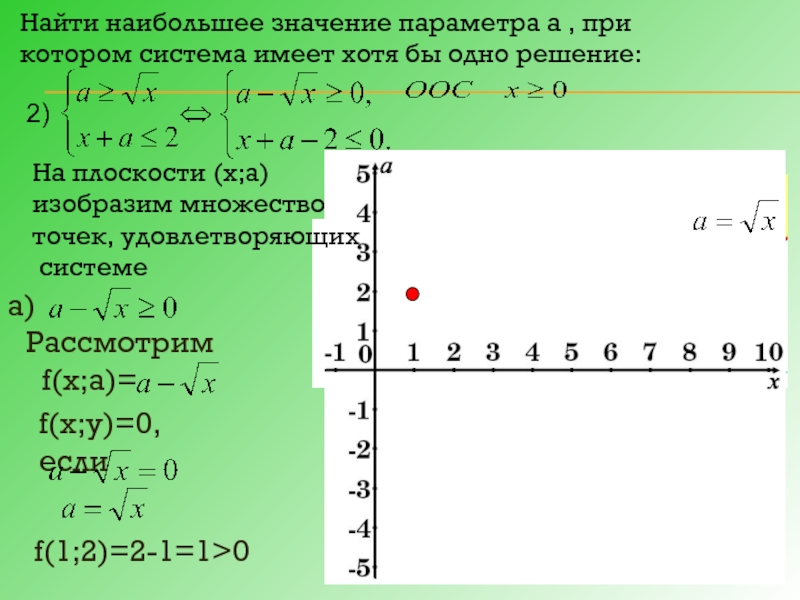
Слайд 17Найти наибольшее значение параметра а , при котором система имеет хотя
бы одно решение:
На плоскости (х;а) изобразим множество
точек, удовлетворяющих
системе
а)
Рассмотрим
f(х;а)=
f(х;у)=0, если
f(1;2)=2-1=1>0
2)
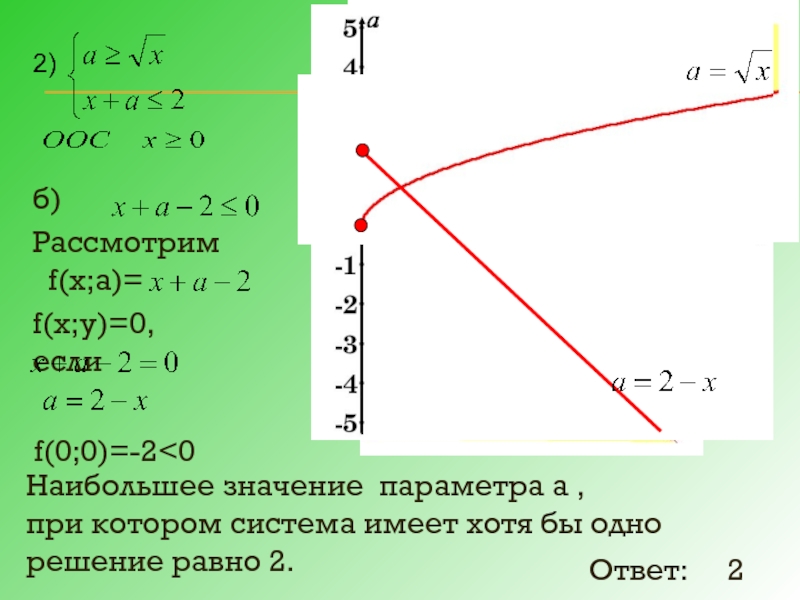
Слайд 18б)
Рассмотрим
f(х;а)=
f(х;у)=0, если
f(0;0)=-2
система имеет хотя бы одно решение равно 2.
Ответ: 2
2)
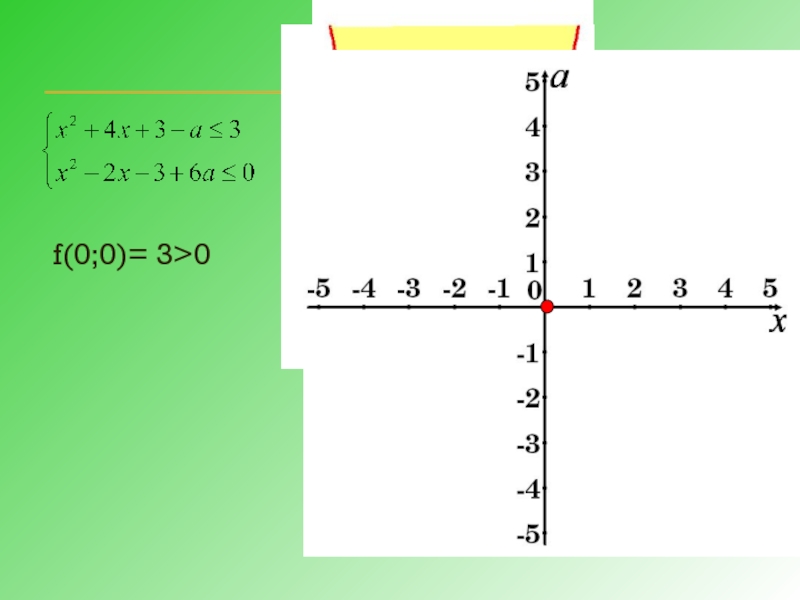
Слайд 19 Найти наименьшее целое значение параметра а , при котором система
имеет единственное решение:
3)
Слайд 20Преобразуем систему:
1) Рассмотрим f(х;а)=
f(х;у)=0, если
Это квадратичная функция, график – парабола,
ветви
вверх, вершина (-2;-1), х=-2 ось cимметрии.
Слайд 222)Рассмотрим f(х;а)=
f(х;у)=0, если
Это квадратичная функция, график – парабола,
ветви вниз, вершина
(1; ), х=1ось cимметрии.
Слайд 25Найдите все значения а , при каждом из которых общие решения
неравенств и образуют на числовой оси отрезок длины единица.
а)
Решение:
Найдем а, при которых система неравенств (1) имеет решения:
Преобразуем систему:
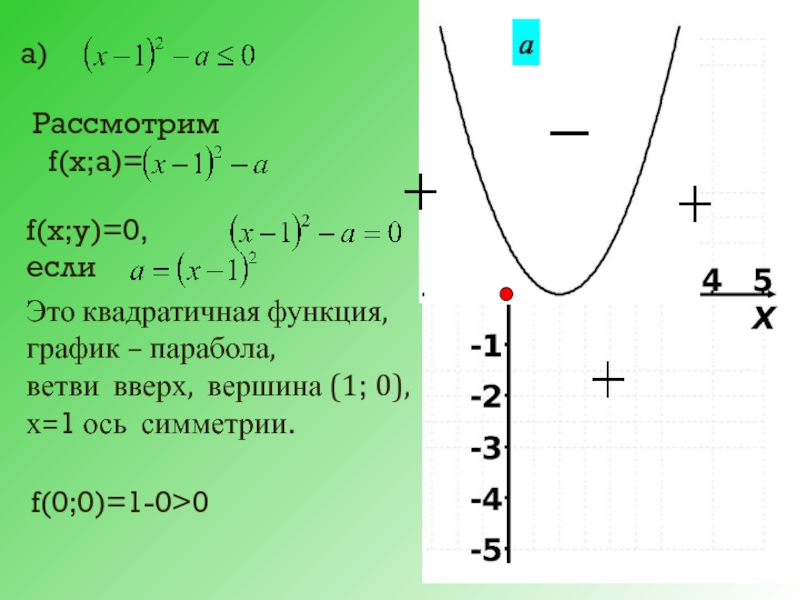
Слайд 26а)
Рассмотрим
f(х;а)=
f(х;у)=0, если
Это квадратичная функция,
график – парабола,
ветви вверх, вершина (1;
0),
х=1 ось симметрии.
х=1 ось симметрии.
f(0;0)=1-0>0
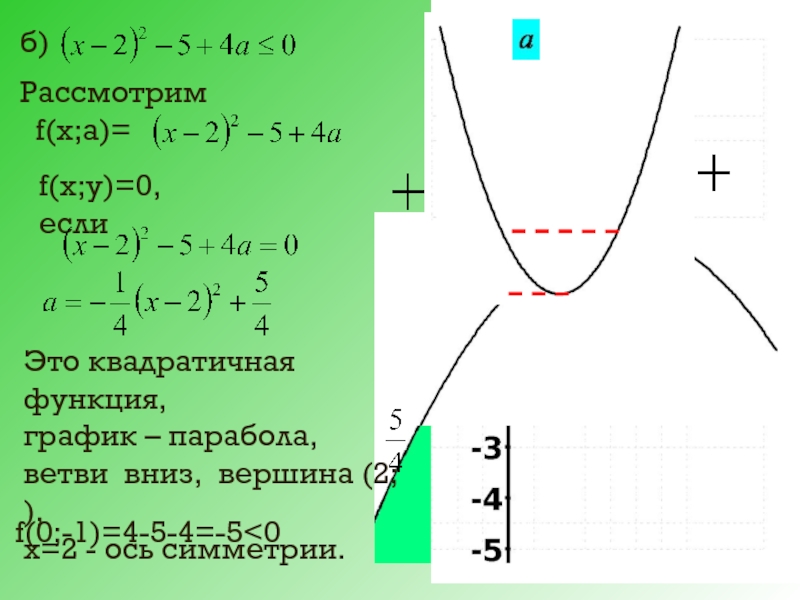
Слайд 27б)
Рассмотрим
f(х;а)=
f(х;у)=0, если
Это квадратичная функция,
график – парабола,
ветви вниз, вершина (2;
),
х=2 - ось cимметрии.
х=2 - ось cимметрии.
f(0;-1)=4-5-4=-5<0
Слайд 28
Система неравенств имеет решение,
если aϵ [0; ].
Решения неравенств
образуют
на числовой оси отрезок длины единица,
при а=1 и а= ¼
при а=1 и а= ¼
а=1
а= ¼
Слайд 29
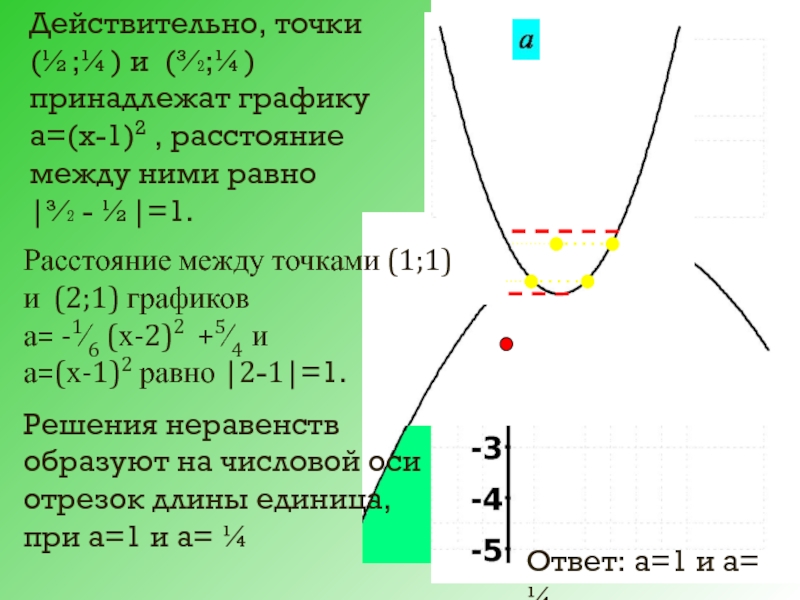
Действительно, точки (½;¼) и (³∕₂;¼) принадлежат графику а=(х-1)2 , расстояние между
ними равно
|³∕₂ - ½|=1.
|³∕₂ - ½|=1.
Решения неравенств
образуют на числовой оси отрезок длины единица,
при а=1 и а= ¼
Ответ: а=1 и а= ¼
Расстояние между точками (1;1) и (2;1) графиков
а= -1∕6 (х-2)2 +5∕4 и
а=(х-1)2 равно |2-1|=1.
Слайд 30Метод областей можно назвать
методом интервалов для плоскости.
Его можно использовать
для
решения заданий ЕГЭ части С .
Таким образом:
Слайд 33При каких значениях параметра «а» , система имеет единственное решение:
Найти наименьшее
значение параметра «а» ,при котором система имеет хотя бы одно решение:
Слайд 34Найти наименьшее целое значение параметра «а» ,при котором система имеет хотя
бы одно решение:
Найти наибольшее значение параметра «а» ,при котором система имеет хотя бы одно решение:
Слайд 35Найти наибольшее целое значение параметра «а» ,при котором система имеет
хотя бы одно решение:
Слайд 36Замечание: метод областей как таковой – лишь иллюстрация. Решение может считаться
обоснованным, только если получены и выписаны уравнения всех линий, изображенных на рисунке, и приведены доказательства правильности расстановки знаков. Рисунок, естественно, должен быть выполнен по возможности аккуратнее. В частности, желательно указать, какие линии входят в рассматриваемое множество, а какие нет.
Слайд 37Список использованной литературы.
Математика для поступающих в серьезные вузы.
О.Ю.Черкасов
, А.Г.Якушев . – M.: Московский лицей, 2009.
ЕГЭ 2010 математика .Федеральный институт педагогических измерений. Официальный разработчик контрольных измерительных материалов для ЕДИНОГО ГОСУДАРСТВЕННОГО ЭКЗАМЕНА.
Общая редакция: А.Л.Семенов, И.В.Ященко.
ЕГЭ 2010 математика .Федеральный институт педагогических измерений. Официальный разработчик контрольных измерительных материалов для ЕДИНОГО ГОСУДАРСТВЕННОГО ЭКЗАМЕНА.
Общая редакция: А.Л.Семенов, И.В.Ященко.
Слайд 38 САФИНА АЛИНА
УЧИТЕЛЬ МАТЕМАТИКИ – ПОТАПОВА Е.А.
ХАРЛАМОВА АНАСТАСИЯ
Вас благодарят
за внимание:
