- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Матрицы. Действия с матрицами презентация
Содержание
- 1. Матрицы. Действия с матрицами
- 2. Основные определения Определение. Матрицей размера m×n, где
- 3. Матрица может состоять как из одной строки,
- 4. Определение. Матрица вида: называется единичной матрицей
- 5. Определение. Если amn = anm , то
- 6. Основные действия над матрицами Сложение
- 7. Определение. Суммой (разностью) матриц является матрица,
- 8. Операция умножения (деления) матрицы любого размера
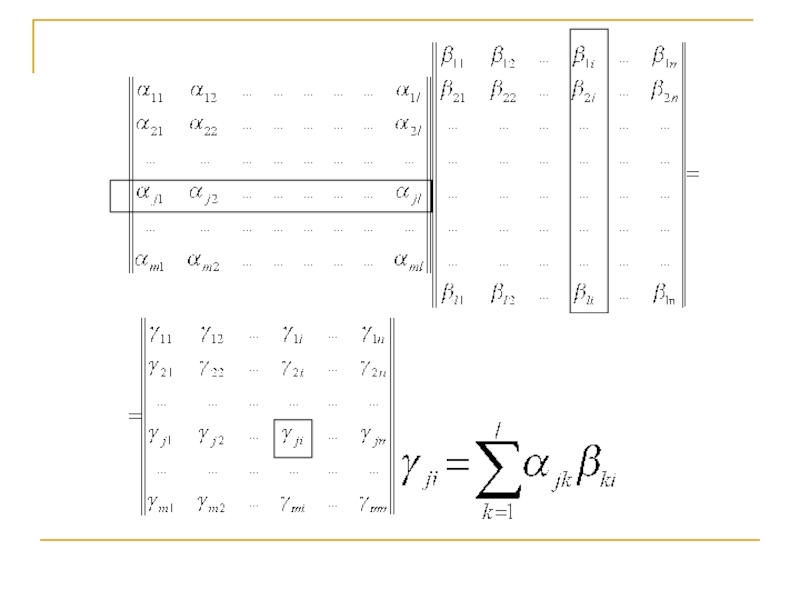
- 9. Операция умножения матриц Определение: Произведением матриц
- 11. Свойства операции умножения матриц 1)Умножение матриц
- 12. 2) Операция перемножения матриц ассоциативна, т.е. если
- 13. 4) Если произведение АВ определено, то для
- 14. Операция транспонирования Транспонированием матрицы называется операция, в
- 15. Для элементов транспонированной матрицы при
- 16. Элементарные преобразования матрицы Определение. Элементарными преобразованиями
- 17. Те же операции, применяемые для столбцов, также
- 18. Обратная матрица Определение. Если существуют квадратные
- 19. НАХОЖДЕНИЕ ОБРАТНОЙ МАТРИЦЫ (1 способ)
- 20. К матрице Aij «дописывают» справа единичную матрицу.
- 21. ПРИМЕНЕНИЕ ОБРАТНОЙ МАТРИЦЫ обратная матрица позволяет найти решения следующих матричных уравнений: АХ=С ХВ=С АХВ=С Решение: Х=А-1С Х=СВ-1 Х=А-1СВ-1
- 22. Замечание: В качестве всех или некоторых
Слайд 2Основные определения
Определение. Матрицей размера m×n, где m- число строк, n- число
Слайд 3Матрица может состоять как из одной строки, так и из одного
Определение. Если число столбцов матрицы равно числу строк (m=n), то матрица называется квадратной
Слайд 5Определение. Если amn = anm , то матрица называется симметрической
Определение. Квадратная
Слайд 6Основные действия над матрицами
Сложение и вычитание матриц сводится к
Слайд 7
Определение. Суммой (разностью) матриц является матрица, элементами которой являются соответственно сумма
cij = aij ± bij
С = А + В = В + А.
Слайд 8 Операция умножения (деления) матрицы любого размера на произвольное число сводится
α (А+В) =αА ± αВ
А(α±β) = αА ± βА
Слайд 9Операция умножения матриц
Определение: Произведением матриц называется матрица, элементы которой могут
A⋅B = C;
Из приведенного определения видно, что операция умножения матриц определена только для матриц, число столбцов первой из которых равно числу строк второй.
Слайд 11Свойства операции умножения матриц
1)Умножение матриц не коммутативно,
т.е. АВ ≠
Перестановочными могут быть только квадратные матрицы одного и того же порядка.
Заметим: А⋅Е = Е⋅А = А
Очевидно, что для любых матриц выполняются следующее свойство:
A⋅O = O; O⋅A = O, где О – нулевая матрица.
Слайд 122) Операция перемножения матриц ассоциативна, т.е. если определены произведения АВ и
(АВ)С=А(ВС).
3) Операция умножения матриц дистрибутивна по отношению к сложению, т.е. если имеют смысл выражения А(В+С) и (А+В)С, то соответственно:
А(В + С) = АВ + АС
(А + В)С = АС + ВС.
Слайд 134) Если произведение АВ определено, то для любого числа α верно
α(AB) = (αA)B = A(αB).
5) Если определено произведение АВ , то определено произведение ВТАТ и выполняется равенство:
(АВ)Т = ВТАТ, где индексом Т обозначается транспонированная матрица.
6) Заметим также, что для любых квадратных матриц det (AB) = detA⋅detB.
(Понятие det (определитель, детерминант) будет рассмотрено ниже).
Слайд 14Операция транспонирования
Транспонированием матрицы называется операция, в результате которой образуется новая матрица,
транспонирование
Слайд 15Для элементов транспонированной матрицы при верно равенство:
Операция транспонирования
.
Слайд 16Элементарные преобразования матрицы
Определение. Элементарными преобразованиями матрицы назовем следующие преобразования:
1) умножение
2) прибавление к элементам одной строки элементов другой строки;
3) перестановка строк;
4) вычеркивание (удаление) одной из одинаковых строк (столбцов);
5) транспонирование.
Слайд 17Те же операции, применяемые для столбцов, также называются элементарными преобразованиями.
С помощью
Слайд 18Обратная матрица
Определение. Если существуют квадратные матрицы Х и А одного
XA = AX = E,
где Е - единичная матрица того же самого порядка, что и матрица А, то матрица Х называется обратной к матрице А и обозначается А-1.
Слайд 20К матрице Aij «дописывают» справа единичную матрицу. С помощью элементарных преобразований