- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Matrices: Basic Operations презентация
Содержание
- 1. Matrices: Basic Operations
- 2. Barnett/Ziegler/Byleen Finite Mathematics 11e Addition and Subtraction
- 3. Barnett/Ziegler/Byleen Finite Mathematics 11e Example: Addition Add the matrices
- 4. Barnett/Ziegler/Byleen Finite Mathematics 11e Example: Addition Solution
- 5. Barnett/Ziegler/Byleen Finite Mathematics 11e Example: Subtraction Now,
- 6. Barnett/Ziegler/Byleen Finite Mathematics 11e Example: Subtraction Solution
- 7. Barnett/Ziegler/Byleen Finite Mathematics 11e Scalar Multiplication The
- 8. Barnett/Ziegler/Byleen Finite Mathematics 11e Example: Scalar Multiplication Find (-1)A, where A =
- 9. Barnett/Ziegler/Byleen Finite Mathematics 11e Example: Scalar Multiplication
- 10. Barnett/Ziegler/Byleen Finite Mathematics 11e Alternate Definition of
- 11. Barnett/Ziegler/Byleen Finite Mathematics 11e Example The example
- 12. Barnett/Ziegler/Byleen Finite Mathematics 11e Matrix Equations Example: Find a, b, c, and d so that
- 13. Barnett/Ziegler/Byleen Finite Mathematics 11e Matrix Equations Example:
- 14. Barnett/Ziegler/Byleen Finite Mathematics 11e Matrix Products
- 15. Barnett/Ziegler/Byleen Finite Mathematics 11e Arthur Cayley 1821-1895 Introduced matrix multiplication
- 16. Barnett/Ziegler/Byleen Finite Mathematics 11e Product of a
- 17. Barnett/Ziegler/Byleen Finite Mathematics 11e Row by Column
- 18. Barnett/Ziegler/Byleen Finite Mathematics 11e Example: Revenue of
- 19. Barnett/Ziegler/Byleen Finite Mathematics 11e Solution using Matrix
- 20. Barnett/Ziegler/Byleen Finite Mathematics 11e Matrix Product
- 21. Barnett/Ziegler/Byleen Finite Mathematics 11e Multiplying a 2x4
- 22. Barnett/Ziegler/Byleen Finite Mathematics 11e Final Result
- 23. Barnett/Ziegler/Byleen Finite Mathematics 11e Undefined Matrix Multiplication
- 24. Barnett/Ziegler/Byleen Finite Mathematics 11e Undefined Matrix Multiplication
- 25. Barnett/Ziegler/Byleen Finite Mathematics 11e Example Given
- 26. Barnett/Ziegler/Byleen Finite Mathematics 11e Solution Since
- 27. Barnett/Ziegler/Byleen Finite Mathematics 11e Is Matrix Multiplication
- 28. Barnett/Ziegler/Byleen Finite Mathematics 11e Practical Application Suppose
- 29. Barnett/Ziegler/Byleen Finite Mathematics 11e Solution of Practical
Слайд 1Barnett/Ziegler/Byleen Finite Mathematics 11e
Learning Objectives for Section 4.4
Matrices: Basic Operations
The
The student will be able to find the scalar product of a number k and a matrix M.
The student will be able to calculate a matrix product.
Слайд 2Barnett/Ziegler/Byleen Finite Mathematics 11e
Addition and Subtraction
of Matrices
To add or
Слайд 4Barnett/Ziegler/Byleen Finite Mathematics 11e
Example: Addition
Solution
Add the matrices
Solution: First note that
Adding corresponding entries, we have
Слайд 5Barnett/Ziegler/Byleen Finite Mathematics 11e
Example: Subtraction
Now, we will subtract the same two
=
Слайд 6Barnett/Ziegler/Byleen Finite Mathematics 11e
Example: Subtraction
Solution
Now, we will subtract the same two
Subtract corresponding entries as follows:
=
Слайд 7Barnett/Ziegler/Byleen Finite Mathematics 11e
Scalar Multiplication
The scalar product of a number k
Слайд 8Barnett/Ziegler/Byleen Finite Mathematics 11e
Example: Scalar Multiplication
Find (-1)A, where A =
Слайд 9Barnett/Ziegler/Byleen Finite Mathematics 11e
Example: Scalar Multiplication
Solution
Find (-1)A, where A =
Solution:
(-1)A=
Слайд 10Barnett/Ziegler/Byleen Finite Mathematics 11e
Alternate Definition of
Subtraction of Matrices
The definition
If A and B are two matrices of the same dimensions, then
A – B = A + (-1)B,
where (-1) is a scalar.
Слайд 11Barnett/Ziegler/Byleen Finite Mathematics 11e
Example
The example on the right illustrates this procedure
Слайд 12Barnett/Ziegler/Byleen Finite Mathematics 11e
Matrix Equations
Example: Find a, b, c, and d
Слайд 13Barnett/Ziegler/Byleen Finite Mathematics 11e
Matrix Equations
Example: Find a, b, c, and d
Solution: Subtract the matrices on the left side:
Use the definition of equality to change this matrix equation into 4 real number equations:
a - 2 = 4 b + 1 = 3 c + 5 = -2 d - 6 = 4 a = 6 b = 2 c = -7 d = 10
Слайд 14Barnett/Ziegler/Byleen Finite Mathematics 11e
Matrix Products
The method of multiplication of matrices
Matrix multiplication was introduced by an English mathematician named Arthur Cayley (1821-1895). We will see shortly how matrix multiplication can be used to solve systems of linear equations.
Слайд 15Barnett/Ziegler/Byleen Finite Mathematics 11e
Arthur Cayley
1821-1895
Introduced matrix multiplication
Слайд 16Barnett/Ziegler/Byleen Finite Mathematics 11e
Product of a Row Matrix
and a Column
In order to understand the general procedure of matrix multiplication, we will introduce the concept of the product of a row matrix by a column matrix.
A row matrix consists of a single row of numbers, while a column matrix consists of a single column of numbers. If the number of columns of a row matrix equals the number of rows of a column matrix, the product of a row matrix and column matrix is defined. Otherwise, the product is not defined.
Слайд 17Barnett/Ziegler/Byleen Finite Mathematics 11e
Row by Column Multiplication
Example: A row matrix consists
1x4 row matrix multiplied by a 4x1 column matrix. Notice the manner in which corresponding entries of each matrix are multiplied:
Слайд 18Barnett/Ziegler/Byleen Finite Mathematics 11e
Example:
Revenue of a Car Dealer
A car dealer sells
Слайд 19Barnett/Ziegler/Byleen Finite Mathematics 11e
Solution using Matrix Multiplication
We represent the number of
Слайд 20Barnett/Ziegler/Byleen Finite Mathematics 11e
Matrix Product
If A is an m x
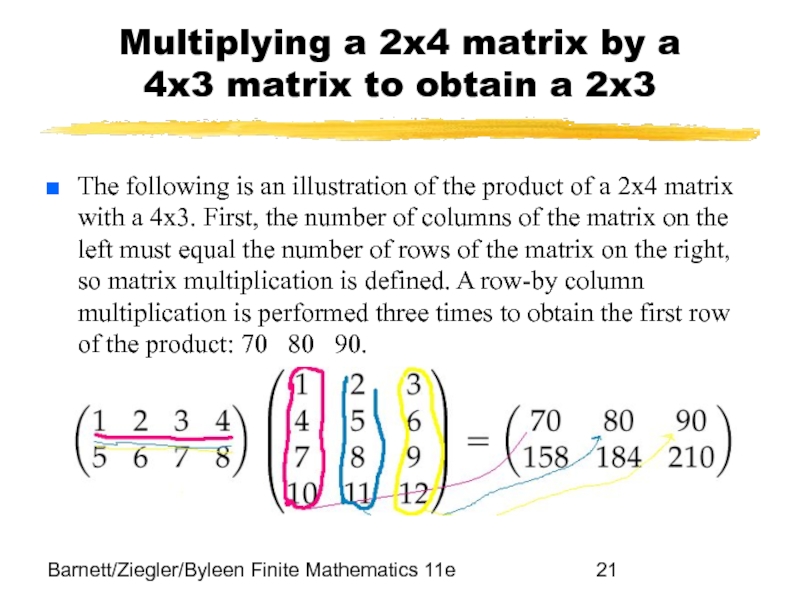
Слайд 21Barnett/Ziegler/Byleen Finite Mathematics 11e
Multiplying a 2x4 matrix by a
4x3 matrix
The following is an illustration of the product of a 2x4 matrix with a 4x3. First, the number of columns of the matrix on the left must equal the number of rows of the matrix on the right, so matrix multiplication is defined. A row-by column multiplication is performed three times to obtain the first row of the product: 70 80 90.
Слайд 23Barnett/Ziegler/Byleen Finite Mathematics 11e
Undefined Matrix Multiplication
Why is the matrix multiplication below
Слайд 24Barnett/Ziegler/Byleen Finite Mathematics 11e
Undefined Matrix Multiplication
Solution
Why is the matrix multiplication below
Слайд 25Barnett/Ziegler/Byleen Finite Mathematics 11e
Example
Given A = B =
Find AB if it is
Слайд 26Barnett/Ziegler/Byleen Finite Mathematics 11e
Solution
Since A is a 2 x 3
1. Multiply first row of A by first column of B: 3(1) + 1(3) +(-1)(-2)=8
2. First row of A times second column of B: 3(6)+1(-5)+ (-1)(4)= 9
3. Proceeding as above the final result is
=
Слайд 27Barnett/Ziegler/Byleen Finite Mathematics 11e
Is Matrix Multiplication Commutative?
Now we will attempt
We are multiplying a 3 x 2 matrix by a 2 x 3 matrix. This matrix multiplication is defined, but the result will be a 3 x 3 matrix. Since AB does not equal BA, matrix multiplication is not commutative.
=
Слайд 28Barnett/Ziegler/Byleen Finite Mathematics 11e
Practical Application
Suppose you a business owner and sell
Monday: 3 T-shirts at $10 each, 4 hats at $15 each, and 1 pair of shorts at $20. Tuesday: 4 T-shirts at $10 each, 2 hats at $15 each, and 3 pairs of shorts at $20.
Слайд 29Barnett/Ziegler/Byleen Finite Mathematics 11e
Solution of Practical Application
Represent the information using two
Then your total revenue for the two days is = [110 130] Price times Quantity = Revenue
Unit price of each item:
Qty sold of each item on Monday
Qty sold of each item on Tuesday