геометрия
Преобразования координат
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математика. Поточная практика 7.3. Аналитическая геометрия. Преобразования координат презентация
Содержание
- 2. Математика УГТУ-УПИ 2007г. М.А.Вигура, О.А.Кеда, А.Ф.Рыбалко,
- 3. Цель занятия: 1. Овладеть соответствующим математическим
- 4. Формируемые компетенции по ФГОС:
- 5. Преобразования координат
- 6. 1.Теоретическая часть 2.Задачи 3.Решения задач Оглавление Преобразования координат
- 7. Оглавление:
- 8. Оглавление: Преобразования координат
- 9. Оглавление: Преобразования координат
- 10. Оглавление: Преобразования координат
- 11. Оглавление: Преобразования координат
- 12. Оглавление: Преобразования координат
- 13. Оглавление: Преобразования координат
- 14. Оглавление: Преобразования координат
- 15. Оглавление: Преобразования координат
- 16. Оглавление: Преобразования координат
- 17. Оглавление: Преобразования координат
- 18. Оглавление: Преобразования координат
- 19. Оглавление: Преобразования координат
- 20. Оглавление: Преобразования координат
- 21. Задача №: Оглавление: Преобразования координат
- 22. Решение задачи №: Оглавление: Преобразования координат
- 23. Задача 1 Ответ:
- 24. Задача 2 Ответ: Решение: Оглавление: Преобразования координат
- 25. Задача 3 Ответ:
- 26. Задача 4 Ответ: Эллипс Решение: Оглавление: Преобразования координат
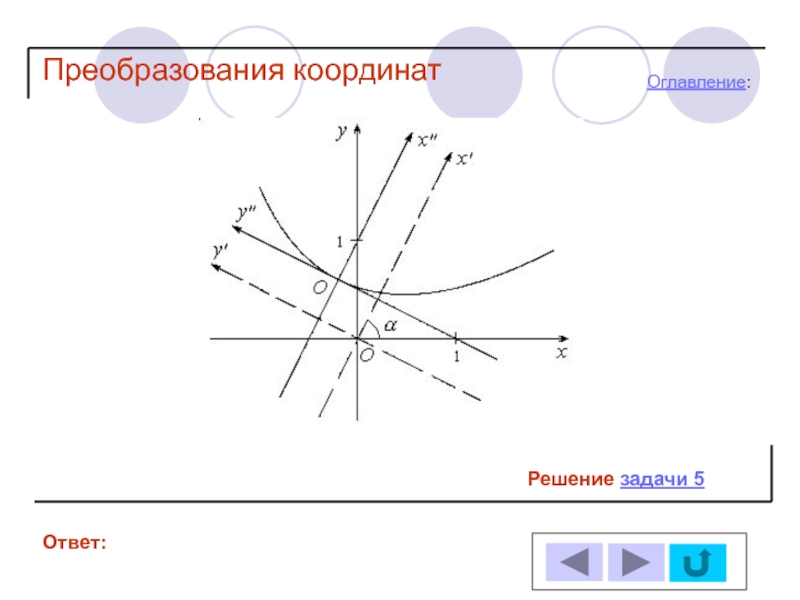
- 27. Задача 5 Ответ: Решение: Оглавление: Преобразования координат
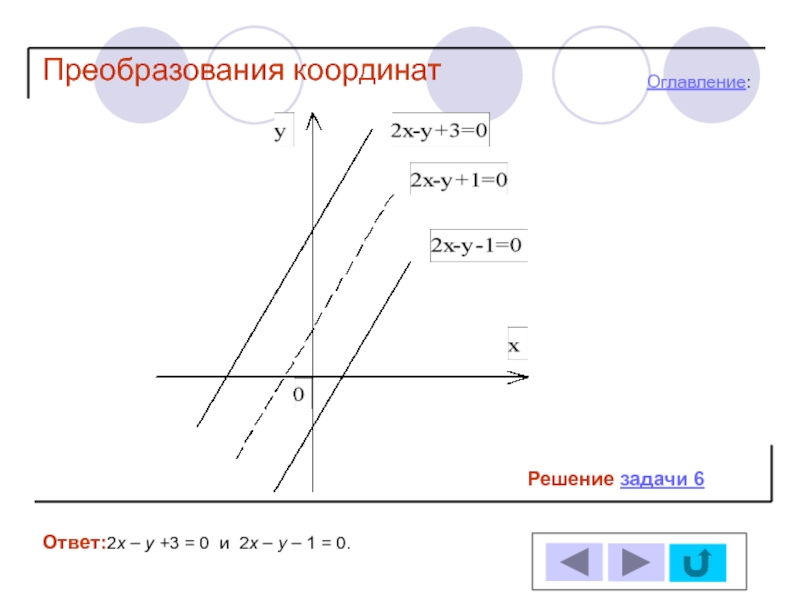
- 28. Задача 6 Ответ: 2х – у +3
- 29. Задача 7 Ответ:
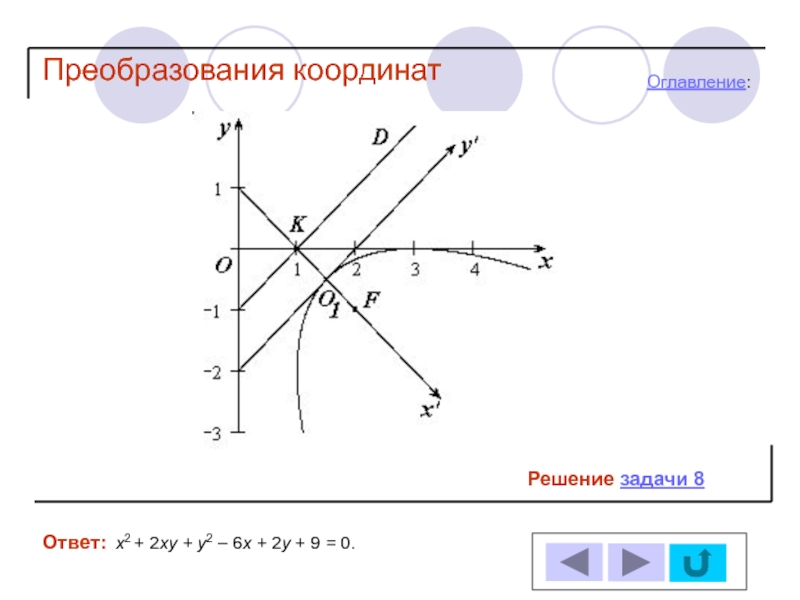
- 30. Задача 8 Ответ:х2 + 2ху + у2
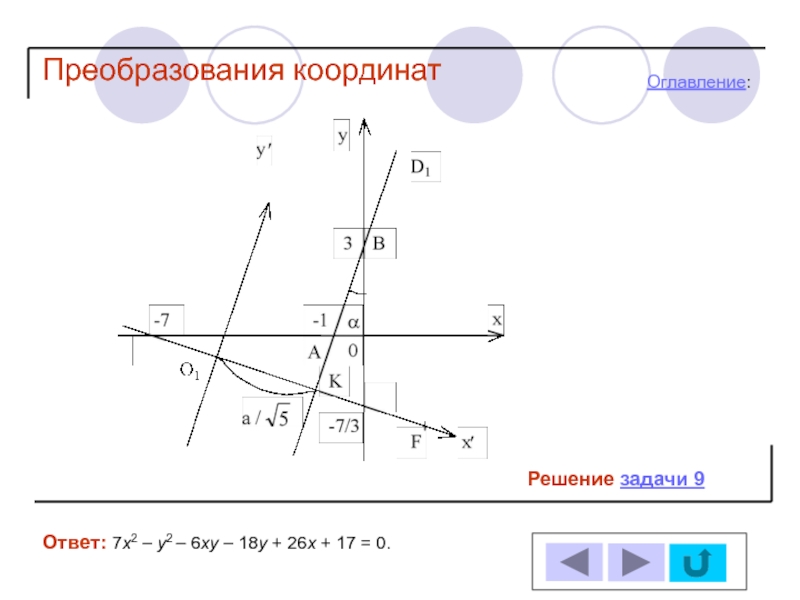
- 31. Задача 9 Ответ: 7х2 – у2 –
- 32. Решение задачи 1 Ответ:
- 33. Решение задачи 2 Ответ: Оглавление: Преобразования координат
- 34. Решение задачи 2 Ответ: Оглавление: Преобразования координат
- 35. Решение задача 3 Ответ:
- 36. Решение задача 3 Ответ:
- 37. Решение задача 4 Ответ:
- 38. Решение задача 4 Ответ:
- 39. Решение задача 4 Ответ:
- 40. Решение задачи 5 Ответ: Оглавление: Преобразования координат
- 41. Решение задачи 5 Ответ: Оглавление: Преобразования координат
- 42. Решение задачи 5 Ответ: Оглавление: Преобразования координат
- 43. Решение задачи 5 Ответ: Оглавление: Преобразования координат
- 44. Решение задачи 5 Ответ: Оглавление: Преобразования координат
- 45. Решение задачи 6 Ответ:2х – у +3
- 46. Решение задачи 6 Ответ:2х – у +3
- 47. Решение задачи 7 Ответ: Мнимый эллипс
- 48. Решение задачи 8 Ответ:
- 49. Решение задачи 8 Ответ:
- 50. Решение задачи 8
- 51. Решение задачи 8
- 52. Решение задачи 9 Ответ:
- 53. Решение задачи 9 Ответ: 7х2 – у2
- 54. Решение задачи 9 Ответ: 7х2 – у2
- 55. Решение задачи 9
- 56. Решение задачи 9
- 57. Решение задачи 9
- 58. Решение задачи 9
- 59. Решение задачи 9 Оглавление:
- 60. В результате студент должен уметь: Записать
- 61. Перечень источников, список дополнительной литературы по
Математика УГТУ-УПИ 2007г. М.А.Вигура, О.А.Кеда, А.Ф.Рыбалко, Н.М.Рыбалко, А.Б.Соболев Поточная практика 7.3 Аналитическая геометрия Преобразования координат
Слайд 2Математика
УГТУ-УПИ
2007г.
М.А.Вигура, О.А.Кеда, А.Ф.Рыбалко,
Н.М.Рыбалко, А.Б.Соболев
Поточная практика 7.3
Аналитическая
Слайд 3Цель занятия: 1. Овладеть соответствующим математическим аппаратом для дальнейшего изучения курса математики,
демонстрировать и использовать математические методы в ходе изучения специальных дисциплин для будущей профессиональной деятельности.
2. Быть в состоянии изобразить кривую второго порядка, найдя координаты, в которых она имеет канонический вид.
Слайд 7
Оглавление:
Преобразования координат
1.Преобразования координат
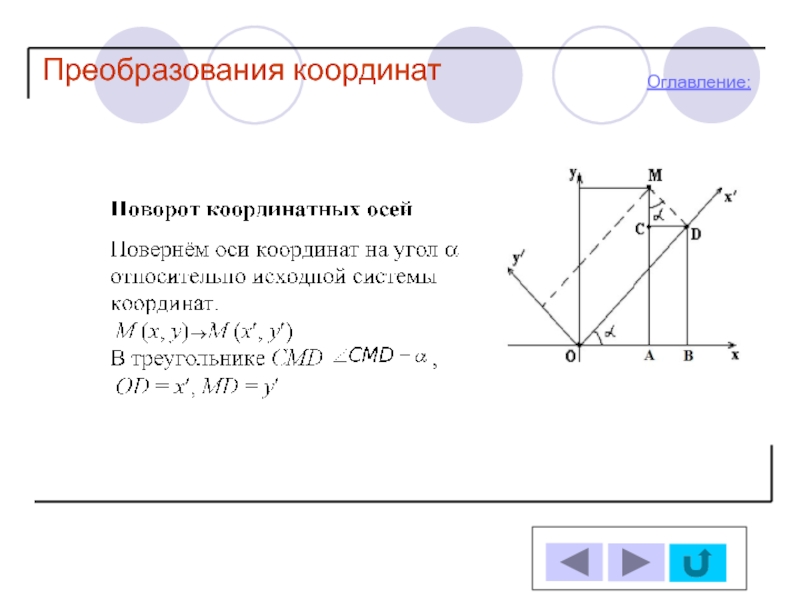
Параллельный перенос
Поворот координатных
осей
Изменение начала координат
и поворот осей
2.Приведение общего уравнения кривой
второго порядка к каноническому виду
Изменение начала координат
и поворот осей
2.Приведение общего уравнения кривой
второго порядка к каноническому виду
Слайд 31Задача 9
Ответ: 7х2 – у2 – 6ху – 18у + 26х
+ 17 = 0.
Решение:
Оглавление:
Преобразования координат
Слайд 52Решение задачи 9
Ответ:
Оглавление:
Преобразования координат
7х2 – у2 – 6ху – 18у +
26х + 17 = 0.
Слайд 53Решение задачи 9
Ответ: 7х2 – у2 – 6ху – 18у +
26х + 17 = 0.
Оглавление:
Преобразования координат
Слайд 54Решение задачи 9
Ответ: 7х2 – у2 – 6ху – 18у +
26х + 17 = 0.
Оглавление:
Преобразования координат
Слайд 55Решение задачи 9
Оглавление:
Ответ: 7х2 – у2 – 6ху – 18у +
26х + 17 = 0.
Преобразования координат
Слайд 56Решение задачи 9
Оглавление:
Ответ: 7х2 – у2 – 6ху – 18у +
26х + 17 = 0.
Преобразования координат
Слайд 57Решение задачи 9
Оглавление:
Ответ: 7х2 – у2 – 6ху – 18у +
26х + 17 = 0.
Преобразования координат
Слайд 58Решение задачи 9
Оглавление:
Ответ: 7х2 – у2 – 6ху – 18у +
26х + 17 = 0.
Преобразования координат
Слайд 59Решение задачи 9
Оглавление:
Ответ: 7х2 – у2 – 6ху – 18у +
26х + 17 = 0.
Преобразования координат
Слайд 60В результате студент должен уметь:
Записать формулы преобразования координат
при параллельном
переносе и повороте осей.
2. Приводить общее уравнение кривой второго порядка к каноническому виду с помощью преобразования координат.
Слайд 61Перечень источников,
список дополнительной литературы по теме.
1. Сборник задач по математике
для втузов: В 4 ч. Ч. 1: Векторная алгебра и аналитическая геометрия. Определители и матрицы системы линейных уравнений. Линейная алгебра. Основы общей алгебры / А. В. Ефимов, А. Ф. Каракулин, И. Б. Кожухов и др. / Под ред. А. В. Ефимова, А. С. Поспелова. - 4-е изд., перераб. и доп. - М.: Физматлит, 2003. - 288 с.: ил.; 21 см. - ISBN 5-940520-34-0.
2. Клетеник, Давид Викторович. Сборник задач по аналитической геометрии: Учеб. пособие для студентов вузов / Под ред. Н.В. Ефимова. - 15-е изд. - М.: Наука. Физматлит, 1998. - 223с. - ISBN 5-02-015080-0.
3. Данко, Павел Ефимович. Высшая математика в упражнениях и задачах: Учеб. пособие для вузов: В 2 ч. Ч. 1 / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. - 6-е изд. - М.: ОНИКС 21 век : Мир и образование, 2003. - 304с.: ил.; 22 см. - ISBN 5-329-00326-1.
4. Элементы аналитической геометрии и линейной алгебры: Сб. комплектов вариантов задач по курсу "Высшая математика". Ч. 1 / Урал. гос. техн. ин-т; Сост. О. А. Белослудцев, М. А. Вигура, Н. В. Кожевников, А. Ф. Рыбалко и др. ; Науч. ред. С. И. Машаров. - Екатеринбург: УГТУ, 1997. - 110 с. - ISBN 5-230-17046-8.
2. Клетеник, Давид Викторович. Сборник задач по аналитической геометрии: Учеб. пособие для студентов вузов / Под ред. Н.В. Ефимова. - 15-е изд. - М.: Наука. Физматлит, 1998. - 223с. - ISBN 5-02-015080-0.
3. Данко, Павел Ефимович. Высшая математика в упражнениях и задачах: Учеб. пособие для вузов: В 2 ч. Ч. 1 / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. - 6-е изд. - М.: ОНИКС 21 век : Мир и образование, 2003. - 304с.: ил.; 22 см. - ISBN 5-329-00326-1.
4. Элементы аналитической геометрии и линейной алгебры: Сб. комплектов вариантов задач по курсу "Высшая математика". Ч. 1 / Урал. гос. техн. ин-т; Сост. О. А. Белослудцев, М. А. Вигура, Н. В. Кожевников, А. Ф. Рыбалко и др. ; Науч. ред. С. И. Машаров. - Екатеринбург: УГТУ, 1997. - 110 с. - ISBN 5-230-17046-8.
