Морозов Нікіта Ігорович
Керівник:
Доцент, кандидат ф.-м. наук, Васильєв Олександр Борисович
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математичні моделі та методи теорії портфеля презентация
Содержание
- 1. Математичні моделі та методи теорії портфеля
- 2. Ціль роботи: Розглянути два способи приведення задач
- 3. Гарри Макс Марко́виц Першим, хто почав розробку
- 4. Задача теорії портфеля: Завдання: Мінімізувати ризик, при
- 5. Теорія портфеля Припустимо, що ми маємо певну
- 6. Теорія портфеля
- 7. Теорія портфеля
- 8. Спосіб 1. Minrisk1m
- 9. Спосіб 1. Maxret1m
- 10. Спосіб 2. Minrisk1u
- 11. Спосіб 2. Maxret1u
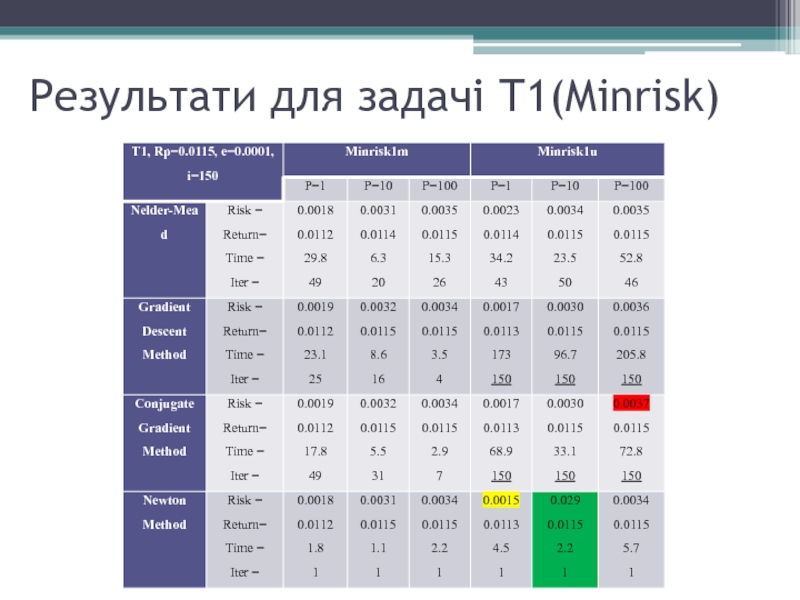
- 12. Результати для задачі Т1(Minrisk)
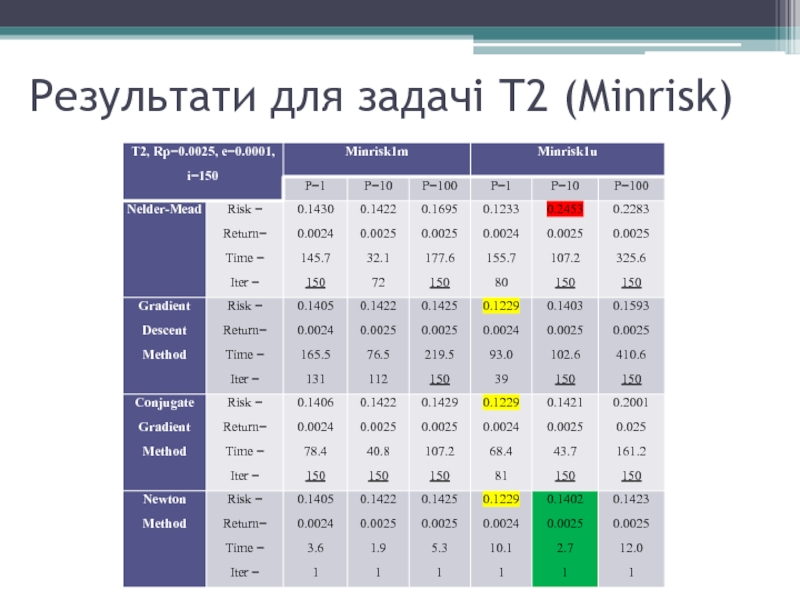
- 13. Результати для задачі Т2 (Minrisk)
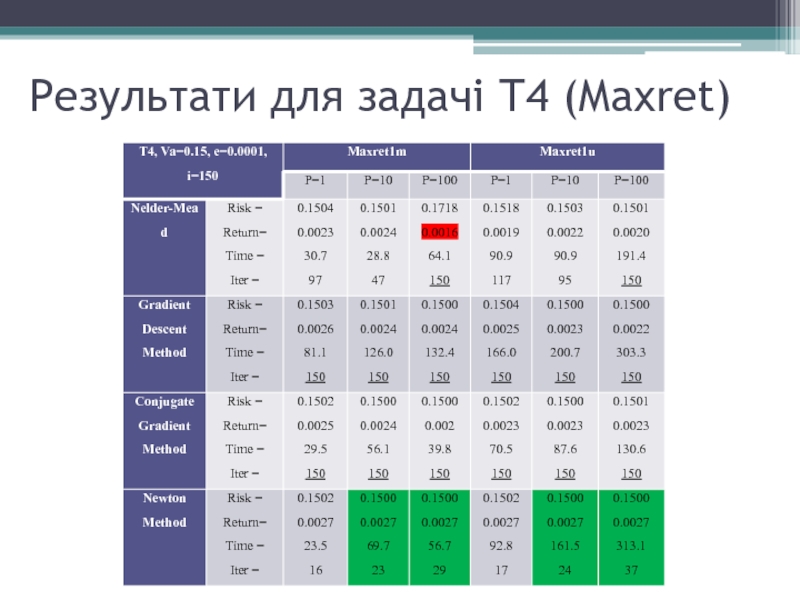
- 14. Результати для задачі Т4 (Maxret)
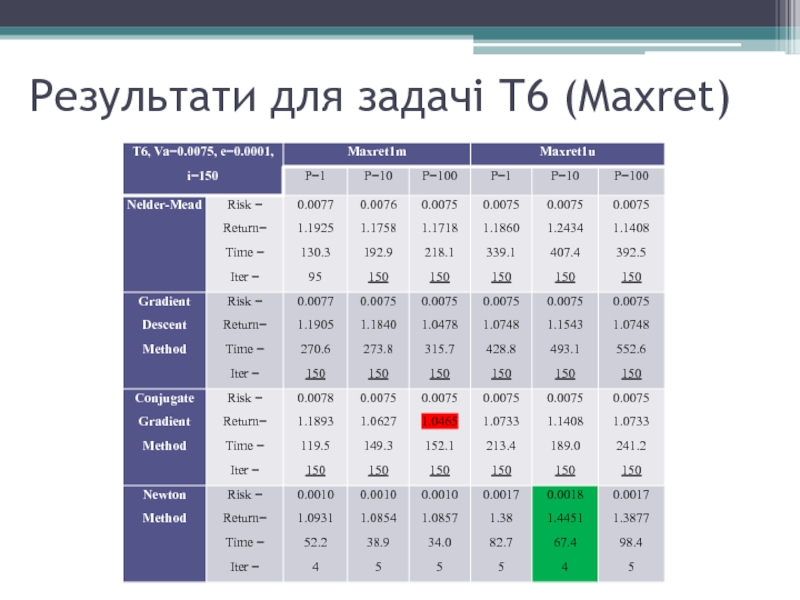
- 15. Результати для задачі Т6 (Maxret)
- 16. Висновки: Спосіб 2: моделі Minrisk1u та Maxret1u
- 17. Дякую за увагу.
Слайд 1Презентація
на тему:
«Математичні моделі та методи теорії портфеля»
Автор роботи:
Студент прикладної математики
Слайд 2Ціль роботи:
Розглянути два способи приведення задач теорії портфеля к задачам безумовної
мінімізації функції.
Спосіб 1: моделі Minrisk1m та Maxret1m.
Спосіб 2: моделі Minrisk1u та Maxret1u.
Застосувати до цих моделей методи мінімізації. Порівняти отримані результати.
Знайти оптимальний спосіб вирішення задач теорії портфеля.
Спосіб 1: моделі Minrisk1m та Maxret1m.
Спосіб 2: моделі Minrisk1u та Maxret1u.
Застосувати до цих моделей методи мінімізації. Порівняти отримані результати.
Знайти оптимальний спосіб вирішення задач теорії портфеля.
Слайд 3Гарри Макс Марко́виц
Першим, хто почав розробку теорії портфеля, був Г. Марковіц.
Основні положення теорії були сформульовані у 1950 – 1951 роках під час підготовки ним докторської дисертації. Пізніше, у 1952 році, Марковіц у статті «Вибір портфеля» оформив і портфельну теорію. У цій статті уперше були запропоновані математичні моделі формування оптимального портфеля, а також методи вирі
За цю теорію Марковіц став лауреатом Нобелівської премії (1990) «за роботи з теорії фінансової економіки».
За цю теорію Марковіц став лауреатом Нобелівської премії (1990) «за роботи з теорії фінансової економіки».
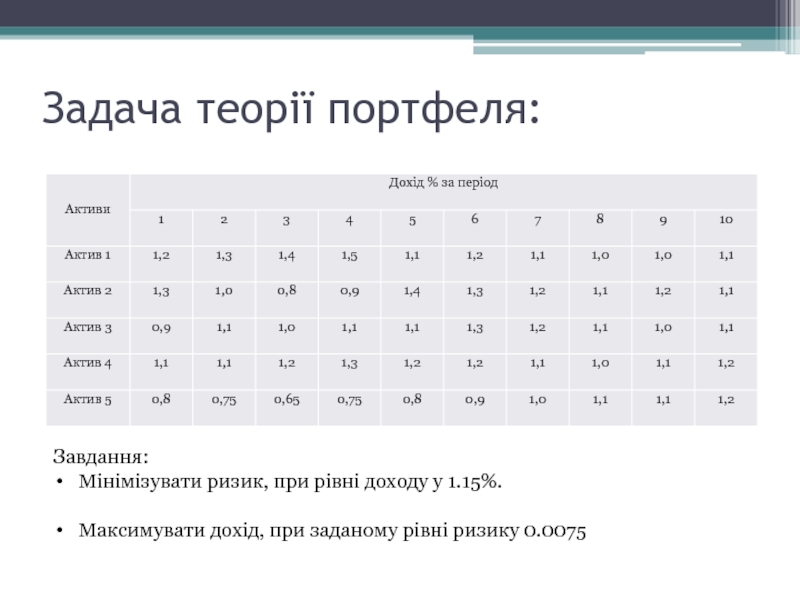
Слайд 4Задача теорії портфеля:
Завдання:
Мінімізувати ризик, при рівні доходу у 1.15%.
Максимувати дохід, при
заданому рівні ризику 0.0075
Слайд 5Теорія портфеля
Припустимо, що ми маємо певну суму коштів М, яку необхідно
розділити між n активами, кожен з яких повертає частину вкладених грошей r в кожен з m періодів часу.
y1,…,yn - співвідношенням інвестицій
Слайд 16Висновки:
Спосіб 2: моделі Minrisk1u та Maxret1u при значенні вагового множника р
= 10 дає найкращі результати але моделі Minrisk1m та Maxret1m вирішуются у середньому швидше.
Найшвидше на усіх зазначених моделях працює метод Ньютона, також він дає найкращі результати.
Найшвидше на усіх зазначених моделях працює метод Ньютона, також він дає найкращі результати.