- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математическое моделирование в электротехнике презентация
Содержание
- 1. Математическое моделирование в электротехнике
- 2. Выписка из учебного плана Лекций – 16
- 3. Самостоятельная работа Самостоятельная работа – это: Подготовка
- 4. Учебно-методическое обеспечение Учебники и учебные пособия, наименования
- 5. Учебники В. Дьяконов MathCAD 2000: учебный
- 6. Учебные пособия Бурулько Л.К., Овчаренко Е.В.
- 7. Мальцева О. П., Кояин Н. В., Удут
- 8. А.В. Аристов, Л. К. Бурулько, Л.А.
- 9. Глазырин А.С. Аналитические методы математического моделирования электромеханических
- 10. Основные разделы дисциплины Основы математического моделирования. Методы
- 11. Основы моделирование в системе MathCAD. Моделирование в системе Matlab/Simulink
- 12. Основы математического моделирования Основные понятия и определения.
- 13. Основные понятия и определения. Основным объектом
- 14. Электротехника – область науки и техники, связанная
- 15. Энергетика – это отрасль промышленности, совокупность больших
- 16. Электромеханика – область науки, изучающая взаимное преобразование
- 17. Электромеханическая система (ЭМС) – это система, осуществляющая
- 18. Оригинал – это объект, подлежащий исследованию, т.
- 19. Подобие – это взаимно-однозначное соответствие между исследуемым
- 20. Виды моделирования. Методы моделирования делятся на две
- 21. Физическое моделирование – это частный случай материального
- 22. Математическое моделирование представляет собой группу методов идеального
- 23. Виды моделей В качестве моделей энергетических и
- 24. Физические модели предназначены для определения численных значений
- 25. При использовании методов моделирования в электромеханике, энергетике
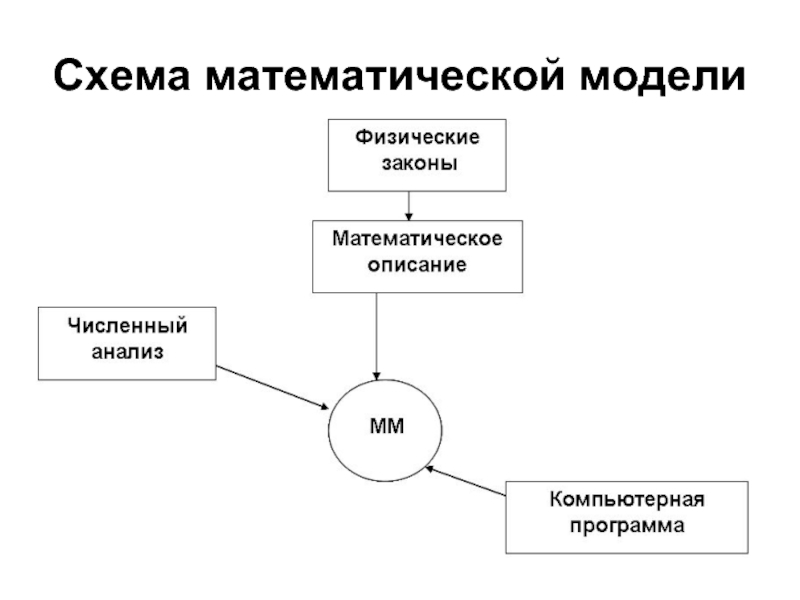
- 26. Схема математической модели
- 27. Математическое описание Математическое описание является одним из
- 28. Численный анализ Решение алгебраических и дифференциальных уравнений
- 29. Компьютерная программа Заключительным этапом построения математической модели
- 30. Выбор метода решения математических уравнений Вторым важным
- 31. классическим методом; операторным методом; численными методами
Слайд 2Выписка из учебного плана
Лекций – 16 ч.
Консультаций – 3 ч.
Лабораторных работ
– 32 ч.
Итоговая аттестация – экзамен
Всего аудиторных занятий – 48 ч.
Самостоятельная работа – 48 ч.
Всего часов на дисциплину – 96 ч.
Итоговая аттестация – экзамен
Всего аудиторных занятий – 48 ч.
Самостоятельная работа – 48 ч.
Всего часов на дисциплину – 96 ч.
Слайд 3Самостоятельная работа
Самостоятельная работа – это:
Подготовка к лабораторным работам;
Подготовка к конференц-неделям;
Проработка отдельных
разделов дисциплины самостоятельно;
Подготовка к экзамену.
Подготовка к экзамену.
Слайд 4Учебно-методическое обеспечение
Учебники и учебные пособия, наименования которых приведены в списке учебной
литературы;
Учебно-методические пособия, разработанные на кафедре ЭПЭО;
Прикладное программное обеспечение: MathCAD 200х; MatLAB; MS-Office Excel 200x; Electronics Workbench; P-CAD;
T-Flex CAD, ELCUT.
Учебно-методические пособия, разработанные на кафедре ЭПЭО;
Прикладное программное обеспечение: MathCAD 200х; MatLAB; MS-Office Excel 200x; Electronics Workbench; P-CAD;
T-Flex CAD, ELCUT.
Слайд 5Учебники
В. Дьяконов MathCAD 2000: учебный курс – СПб.: Питер, 2001.
– 592 с.
В. Дьяконов MatLAB 6: учебный курс – СПб.: Питер, 2001. – 592 с.
В. Дьяконов Simulink - 4: Специальный справочник – СПб.: Питер, 2002. – 528 с.
В. Дьяконов MatLAB 6: учебный курс – СПб.: Питер, 2001. – 592 с.
В. Дьяконов Simulink - 4: Специальный справочник – СПб.: Питер, 2002. – 528 с.
Слайд 6Учебные пособия
Бурулько Л.К., Овчаренко Е.В. Математическое моделирование в электротехнике: Учебное
пособие. – Томск: Изд-во ТПУ, 2003. -100 с.
Бурулько Л.К. Математическое моделирование электромеханических систем. Часть 1 : Математическое моделирование преобразователей электрической энергии переменного тока: Учебное пособие. – Томск: Изд-во ТПУ, 2014. -104 с
Бурулько Л.К. Математическое моделирование электромеханических систем. Часть 1 : Математическое моделирование преобразователей электрической энергии переменного тока: Учебное пособие. – Томск: Изд-во ТПУ, 2014. -104 с
Слайд 7Мальцева О. П., Кояин Н. В., Удут Л. С. Численные методы
в электротехнике: Компьютерный лабораторный практикум/ . – Томск, Изд-во ТПУ 2003. – 100 с.
Бурулько Л.К. Математическое моделирование электромеханических систем. Лабораторный практикум: учебное пособие / Л.К. Бурулько; Томский политехнический университет. – Томск: Изд-во Томского политехнического университета, 2014. – 68 с
Бурулько Л.К. Математическое моделирование электромеханических систем. Лабораторный практикум: учебное пособие / Л.К. Бурулько; Томский политехнический университет. – Томск: Изд-во Томского политехнического университета, 2014. – 68 с
Слайд 8 А.В. Аристов, Л. К. Бурулько, Л.А. Паюк
Математическое моделирование в
электромеханике. Учебное пособие: Томск, Изд-во ТПУ 2005. – 155 с.
Краснов И.Ю. Математическое моделирование в электротехнике: учебное пособие Часть 1 – Томск: Изд-во ТПУ 2009. – 284 с.
Краснов И.Ю. Математическое моделирование в электротехнике: учебное пособие Часть 2 – Томск: Изд-во ТПУ 2009. – 222 с.
Краснов И.Ю. Математическое моделирование в электротехнике: учебное пособие Часть 1 – Томск: Изд-во ТПУ 2009. – 284 с.
Краснов И.Ю. Математическое моделирование в электротехнике: учебное пособие Часть 2 – Томск: Изд-во ТПУ 2009. – 222 с.
Слайд 9Глазырин А.С. Аналитические методы математического моделирования электромеханических систем: учебное пособие –
Томск: Изд-во ТПУ, 2009. – 204 с.
Слайд 10Основные разделы дисциплины
Основы математического моделирования.
Методы решения систем алгебраических и дифференциальных уравнений,
описывающих статику и динамику линейных электрических цепей и электромеханических систем.
Математические модели электрических систем и их элементов.
Математические модели электрических систем и их элементов.
Слайд 12Основы математического моделирования
Основные понятия и определения.
Виды математических моделей.
Построение математических моделей.
Алгоритмы
решения математических моделей
Слайд 13Основные понятия и определения.
Основным объектом исследования, изучения с помощью метода математического
моделирования являются электромеханические системы, широко используемые в таких областях науки и техники, как энергетика, электромеханика и электротехника.
Слайд 14Электротехника – область науки и техники, связанная с применением электрических и
магнитных явлений для преобразования энергии, получения и изменения химического состава веществ, производства и обработки материалов, передачи информации, охватывающая вопросы получения, преобразования и использования электрической энергии в практической деятельности человека
Слайд 15Энергетика – это отрасль промышленности, совокупность больших естественных и искусственных подсистем,
служащих для преобразования, распределения и использования энергетических ресурсов всех видов. Основной задачей энергетики и входящих в нее структур – обеспечение производства электрической или тепловой энергии.
Слайд 16Электромеханика – область науки, изучающая взаимное преобразование механической и электрической энергии,
а также преобразование электрической энергии с одними параметрами в электрическую энергию с другими параметрами. В настоящее время основным объектом электромеханики, как специфического отдела электротехники, являются не постройка и эксплуатация электрических двигателей и машин, а создание и эксплуатация электромеханических систем, обеспечивающих движение различных транспортных средств: автомобилей, электровозов, самолетов, и автоматизацию современных технологических объектов.
Слайд 17Электромеханическая система (ЭМС) – это система, осуществляющая преобразование электрической энергии в
механическую энергию и наоборот.
Моделирование как философская категория – это метод опосредованного познания. Понятие моделирования непосредственно связано с такими понятиями как оригинал, модель, подобие.
Моделирование как философская категория – это метод опосредованного познания. Понятие моделирования непосредственно связано с такими понятиями как оригинал, модель, подобие.
Слайд 18Оригинал – это объект, подлежащий исследованию, т. е. реально существующий или
проектируемый объект, а также явление, режим или процесс.
Модель – аналог оригинала, т. е. вспомогательный объект, находящийся в определенном соответствии с оригиналом, но более удобный для решения задачи конкретного исследования.
Между моделью и оригиналом должно существовать известное подобие. Оно заключается или в сходстве физических характеристик модели и оригинала, или в сходстве выполняемых функций, либо в тождестве поведения модели и оригинала. Таким образом, понятие модели всегда требует введение понятия подобия.
Модель – аналог оригинала, т. е. вспомогательный объект, находящийся в определенном соответствии с оригиналом, но более удобный для решения задачи конкретного исследования.
Между моделью и оригиналом должно существовать известное подобие. Оно заключается или в сходстве физических характеристик модели и оригинала, или в сходстве выполняемых функций, либо в тождестве поведения модели и оригинала. Таким образом, понятие модели всегда требует введение понятия подобия.
Слайд 19Подобие – это взаимно-однозначное соответствие между исследуемым объектом (моделью) и оригиналом,
при котором правила перехода от параметров модели к параметрам оригинала известны, а математическое описание допускает их преобразование к тождественному виду.
Моделирование как процесс содержит в себя три элемента:
1. субъект (исследователь),
2. объект исследования,
3. модель, определяющую (отражающую) отношения познающего субъекта и познаваемого объекта.
Моделирование как процесс содержит в себя три элемента:
1. субъект (исследователь),
2. объект исследования,
3. модель, определяющую (отражающую) отношения познающего субъекта и познаваемого объекта.
Слайд 20Виды моделирования.
Методы моделирования делятся на две группы: материальное (предметное) и идеальное
моделирование. Материальное моделирование основано на материальной аналогии объекта и модели. Оно осуществляется с помощью воспроизведения основных геометрических, физических или функциональных характеристик изучаемого объекта.
Слайд 21Физическое моделирование – это частный случай материального моделирования, когда модель и
моделируемый объект имеют одну и ту же физическую природу. Физические модели воспроизводят весь комплекс свойств изучаемых явлений. При физическом моделировании в дополнение к геометрическому подобию предусматривается подобие скоростей, сил, материальных сред и т. д.
Слайд 22Математическое моделирование представляет собой группу методов идеального моделирования. Математическое моделирование осуществляется
средствами логико-математических построений математических моделей.
Математическая модель – это описание оригинала с помощью математической символики. Это система математических объектов (чисел, переменных, матриц, множеств и т. п.) и отношений между ними, которые характеризуют некоторые свойства оригинала.
Математическая модель – это описание оригинала с помощью математической символики. Это система математических объектов (чисел, переменных, матриц, множеств и т. п.) и отношений между ними, которые характеризуют некоторые свойства оригинала.
Слайд 23Виды моделей
В качестве моделей энергетических и электромеханических систем различают модели физические,
математические и геометрические.
Геометрические модели дают внешнее представление оригинала и большей частью служат для демонстрационных целей. Они показывают принцип действия, взаимное расположение объектов в процессе сборки, компоновку.
Геометрические модели дают внешнее представление оригинала и большей частью служат для демонстрационных целей. Они показывают принцип действия, взаимное расположение объектов в процессе сборки, компоновку.
Слайд 24Физические модели предназначены для определения численных значений величин, характеризующих поведение реального
объекта путем измерения соответствующих величин в модели.
Физическая модель – это модель, выполненная из конкретных материалов по определенной технологии и с соблюдением геометрических соотношений (либо пропорций). Она максимально отражает физические процессы в исследуемом объекте.
Физическая модель – это модель, выполненная из конкретных материалов по определенной технологии и с соблюдением геометрических соотношений (либо пропорций). Она максимально отражает физические процессы в исследуемом объекте.
Слайд 25При использовании методов моделирования в электромеханике, энергетике и электротехнике, как показывает
практика, наиболее эффективным и универсальным инструментом исследователя и инженера при решении задач анализа, синтеза и управления электромеханическими и энергетическими системами и установками является
метод математического моделирования.
метод математического моделирования.
Слайд 27Математическое описание
Математическое описание является одним из основных этапов моделирования.
Математическое описание состоит
из двух подсистем уравнений – компонентной и топологической.
Топологические уравнения – это системы алгебраических и дифференциальных уравнений.
Это уравнения электрического и механического равновесия, составляемые на основе законов Кирхгофа и Ньютона.
Уравнения отдельных элементов схемы называются компонентными
Топологические уравнения – это системы алгебраических и дифференциальных уравнений.
Это уравнения электрического и механического равновесия, составляемые на основе законов Кирхгофа и Ньютона.
Уравнения отдельных элементов схемы называются компонентными
Слайд 28Численный анализ
Решение алгебраических и дифференциальных уравнений реализуется с использованием численных методов.
Эффективность моделирования при этом оценивают по двум показателям — точности и быстроте нахождения решения.
Обычно между ними существует противоречие: для повышения точности уменьшают шаг интегрирования, но при этом увеличивается время счёта.
Слайд 29Компьютерная программа
Заключительным этапом построения математической модели является подготовка алгоритма и пользовательской
программы с учетом типа ЭВМ, характерных ее особенностей и прикладного программного обеспечения, типа MathGAD, MatLAB, Elcut, Multisim и т.д.
Слайд 30Выбор метода решения математических уравнений
Вторым важным моментом при математическом моделировании является
решение уравнений, описывающих процессы в системе. В зависимости от сложности полученного математического описания процессов в рассматриваемой системе и конечной цели исследований решение уравнений можно осуществлять: