- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математическое моделирование презентация
Содержание
- 1. Математическое моделирование
- 2. Пусть вам надо решить какую-либо задачу и
- 3. Нужно разобраться: - что дано -
- 4. Предположения, которые позволяют выделить исходные данные, определить,
- 5. Понятие математической модели.
- 6. Когда модель может отображать реальность в абстрактной
- 7. Математическая модель выражает существенные черты объекта или процесса языком уравнений и других математических средств.
- 8. Под математической моделью понимают систему математических соотношений
- 9. При математическом моделировании исследование объекта осуществляется посредством
- 10. Пример Определить площадь поверхности письменного стола.
- 11. Этапы решения задач на компьютере
- 12. 1. Постановка задачи — точная формулировка
- 13. 3. Разработка алгоритма. 4. Запись алгоритма
- 14. Задача 1. На научный семинар собрались ученые
- 15. Постановка задачи. Пусть х — количество
- 16. Математическая модель n = х(х -
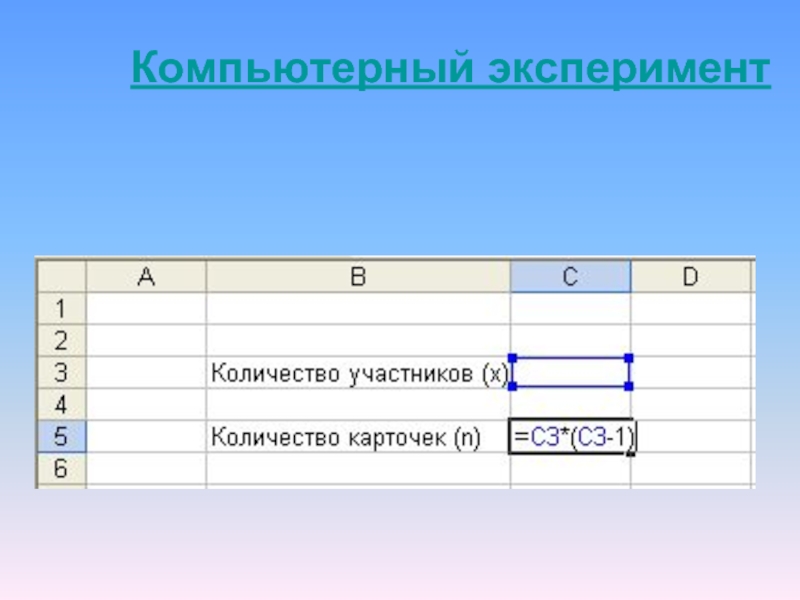
- 17. Компьютерный эксперимент
- 18. Анализ полученных результатов. Проверим результат, решив
- 19. Задание Участники шахматного турнира после окончания
Слайд 2Пусть вам надо решить какую-либо задачу и вы хотите воспользоваться для
этого помощью ЭВМ.
С чего начать?
С чего начать?
Слайд 3Нужно разобраться:
- что дано
- что требуется получить
-как связаны исходные
данные и результаты.
Слайд 4Предположения, которые позволяют выделить исходные данные, определить, что будет служить результатом
и какова связь между исходными данными и результатом, называют
моделью задачи.
Слайд 6Когда модель может отображать реальность в абстрактной форме, почти всегда привлекаются
средства математики,
и мы имеем дело с математической моделью.
Слайд 7Математическая модель выражает существенные черты объекта или процесса языком уравнений и
других математических средств.
Слайд 8Под математической моделью понимают систему математических соотношений — формул, уравнений, неравенств
и т. д., отражающих существенные свойства объекта или процесса.
Слайд 9При математическом моделировании исследование объекта осуществляется посредством изучения модели, сформулированной на
языке математики, с использованием тех или иных методов.
Слайд 10Пример
Определить площадь поверхности письменного стола.
Как обычно поступают в таком
случае?
Измеряют длину и ширину стола, а затем перемножают полученные числа
Измеряют длину и ширину стола, а затем перемножают полученные числа
Слайд 121. Постановка задачи — точная формулировка условий и целей решения, описание
наиболее существенных свойств объекта.
2. Построение математической модели — описание наиболее существенных свойств объекта с помощью математических формул.
2. Построение математической модели — описание наиболее существенных свойств объекта с помощью математических формул.
Слайд 133. Разработка алгоритма.
4. Запись алгоритма на языке программирования.
5. Отладка и тестирование
программы на компьютере.
6. Анализ полученных результатов.
6. Анализ полученных результатов.
Слайд 14Задача 1.
На научный семинар собрались ученые и обменялись друг с другом
визитными карточками. Всего было роздано 210 визитных карточек.
Сколько ученых приехало на семинар, если известно, что их было не более 20?
Сколько ученых приехало на семинар, если известно, что их было не более 20?
Слайд 15Постановка задачи.
Пусть х — количество ученых, приехавших на семинар.
Так как
в процессе обмена каждый раздает по одной карточке всем, кроме себя, то он раздаст (х - 1) карточку.
Следовательно, всего будет роздано n = х • (х — 1) карточек.
Следовательно, всего будет роздано n = х • (х — 1) карточек.
Слайд 18Анализ полученных результатов.
Проверим результат, решив уравнение
х (х - 1) = 210.
х2
- х - 210 = 0.
х =15; -14.
Удовлетворяющий условию задачи корень уравнения х = 15.
ОТВЕТ: 15 человек
х =15; -14.
Удовлетворяющий условию задачи корень уравнения х = 15.
ОТВЕТ: 15 человек
Слайд 19Задание
Участники шахматного турнира после окончания очередной партии обменивались друг с
другом рукопожатиями. Всего сыграно 210 партий, значит, 210 раз противники жали друг другу руки.
Сколько человек принимали участие в турнире, если каждый сыграл по одному разу со всеми остальными и известно, что участников было не более 30?