- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математический аппарат физики презентация
Содержание
- 1. Математический аппарат физики
- 2. «Ни одна из естественных наук, если дело
- 3. Стандартный вид числа
- 4. Свойства степени
- 5. Приставки и множители для образования десятичных кратных
- 6. Таблица приставок и множителей
- 7. Для запоминания наиболее употребляемых в физике приставок
- 8. Приближенные вычисления в задачах по физике Значащие
- 9. Правила округления: Если первая отбрасываемая цифра больше
- 10. Математические действия с приближенными числами – правила
- 11. Решение уравнений первой степени с одним неизвестным.
- 12. Решения уравнения вида – пропорции (уравнение с
- 13. Решите уравнения:
- 14. Квадратные уравнения Уравнения вида
- 15. Неполное квадратное уравнение Дано уравнение
- 16. Система уравнений При решении задач по физике
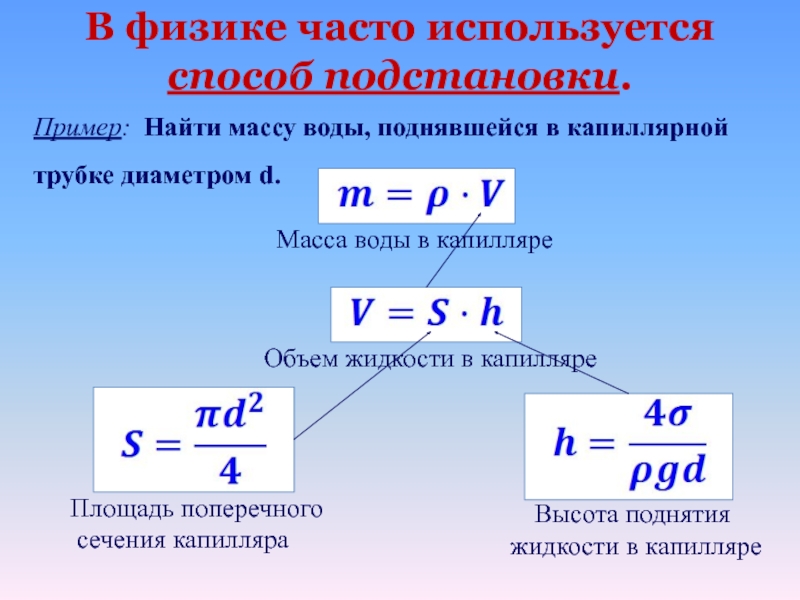
- 17. В физике часто используется способ подстановки. Пример:
- 18. Способ аналогии (сравнения) № 351-Л.
Слайд 2«Ни одна из естественных наук, если дело не идет о собрании
Что касается физики, поставленной впереди других наук…то в настоящее время математика и физика до такой степени слились в одно целое, что иногда трудно отделить – где кончается физика и начинается математика».
Русский ученый В. А. Стеклов
Слайд 3Стандартный вид числа
Любое большое или
Слайд 5Приставки и множители для образования десятичных кратных и дольных единиц.
При изучения
Поэтому принято единицы измерения физических величин записывать с помощью стандартного вида числа или с помощью приставок и множителей.
Например:
Слайд 7Для запоминания наиболее употребляемых в физике приставок используется следующий мнемонический прием:
для
для увеличительных приставок:
«миминапифем»
по звучанию напоминающее греческое слово.
«кимегите»
по звучанию напоминает
японское слово
Слайд 8Приближенные вычисления в задачах по физике
Значащие цифры числа.
Значащими цифрами числа называются
а) 0,00 630 400 б) 8 030 000
Слайд 9Правила округления:
Если первая отбрасываемая цифра больше 4, то последняя сохраняемая цифра
Например, при округлении до сотых 46,2872 ≈ 46,29.
Если первая отбрасываемая цифра меньше 4 или равна 4, то последняя сохраняемая цифра не изменяется.
Например, при округлении до сотых 13,924 ≈ 13,92.
Если отбрасываемая часть числа состоит из одной цифры 5, то число округляется так, чтобы последняя сохраняемая цифра была четной.
Например, при округлении до десятых:
43,25 ≈ 43,2; 43, 35 ≈ 43,4
Слайд 10Математические действия с приближенными числами – правила подсчета цифр.
При сложении и
При умножении и делении в результате сохраняют столько значащих цифр, сколько их имеет приближенное число с наименьшим количеством значащих цифр (без нулей).
Примеры: а) 3,2·12,56 ≈ 40,192 ≈ 40,2; б) 243,25 : 11,2 ≈ 21,7
Результат подсчета значений функций некоторого приближенного числа x должен содержать столько значащих цифр, сколько их содержит число x.
Примеры:
Если некоторые приближенные числа имеют больше десятичных знаков (при сложении или вычитании) или больше значащих цифр (при умножении, делении, возведении в степень, извлечении корня), чем другие, то их предварительно следует округлять, сохраняя только одну лишнюю цифру.
а) 103,7 - 21, 3385 ≈ 82,4; б) 1,2 · 37,82 · 27,425 ≈ 1,2 ·
Слайд 11Решение уравнений первой степени с одним неизвестным.
Для решения уравнений необходимо уметь:
Освобождаться
Из уравнения записанного в строчку, определить нужный параметр.
Решение уравнений вида
Мнемоническое правило решения: «Неизвестное равно: то что находится за знаком равенства, разделить на коэффициент перед неизвестным». Проверить на простом выражении
Слайд 12Решения уравнения вида – пропорции
(уравнение с дробью справа и слева).
Мнемоническое правило
«Перемножим обе части уравнения крест на крест»
Слайд 14Квадратные уравнения
Уравнения вида
Корни квадратного уравнения находят по формуле:
Слайд 16Система уравнений
При решении задач по физике необходимо уметь решать системы двух
При решении систем уравнений используется несколько основных способов:
Способ алгебраического сложения;
Способ подстановки;
Способ сравнения (аналогии) и другие.
Слайд 17В физике часто используется способ подстановки.
Пример: Найти массу воды, поднявшейся в
Слайд 18Способ аналогии (сравнения)
№ 351-Л. Пружина динамометра под действием
Ответ: 12,8 Н