- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математический анализ. Множества. Числовые последовательности презентация
Содержание
- 1. Математический анализ. Множества. Числовые последовательности
- 2. Логическая символика
- 3. 1 Понятие множества Множество (set) – некоторая,
- 4. Примеры множеств
- 5. Объекты, которые образуют множество, называются его элементами.
- 6. Обозначения В дальнейшем множества будем обозначать прописными
- 7. Множество, не содержащее ни одного элемента, называется
- 8. Множество B называется подмножеством множества A, если
- 9. Два множества А и В называются равными,
- 10. Универсальное множество U есть совокупность всех рассматриваемых
- 11. Числовые множества N ={1, 2, 3…} –
- 12. 2 Операции над множествами 2-1 Объединение (сумма)
- 13. Объединением (суммой) двух множеств А и В
- 14. Пересечением (произведением) двух множеств А и В
- 15. Разностью двух множеств А и В называется
- 16. Симметрической разностью двух множеств А и В
- 17. Дополнением к множеству A называется множество элементов
- 18. Для введенных операций присущи следующие свойства: 2-6 Свойства операций над множествами
- 19. 3 Числовые промежутки и ограниченные множества
- 20. Числовые промежутки
- 21. Окрестность точки (neighborhood of point) Абсолютная
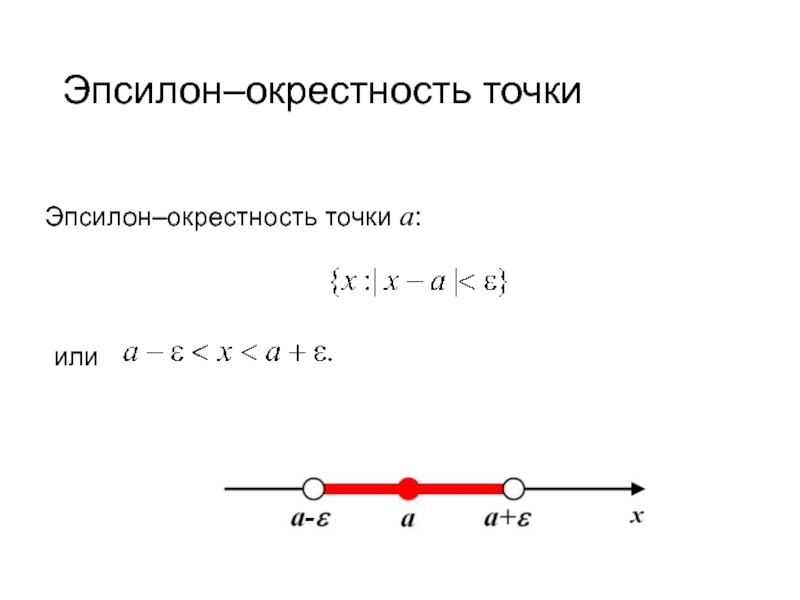
- 22. Эпсилон–окрестность точки Эпсилон–окрестность точки a: или .
- 23. Ограниченные множества
- 24. Если множество Х ограничено сверху, то говорят,
- 25. Задача. Найти точную верхнюю и точную нижнюю
- 26. С другой стороны, наименьший элемент для рассматриваемого
- 27. 4 Числовые последовательности 1 Определение последовательности 2
- 28. 4-1 Определение последовательности Если каждому натуральному числу
- 29. Примеры последовательностей
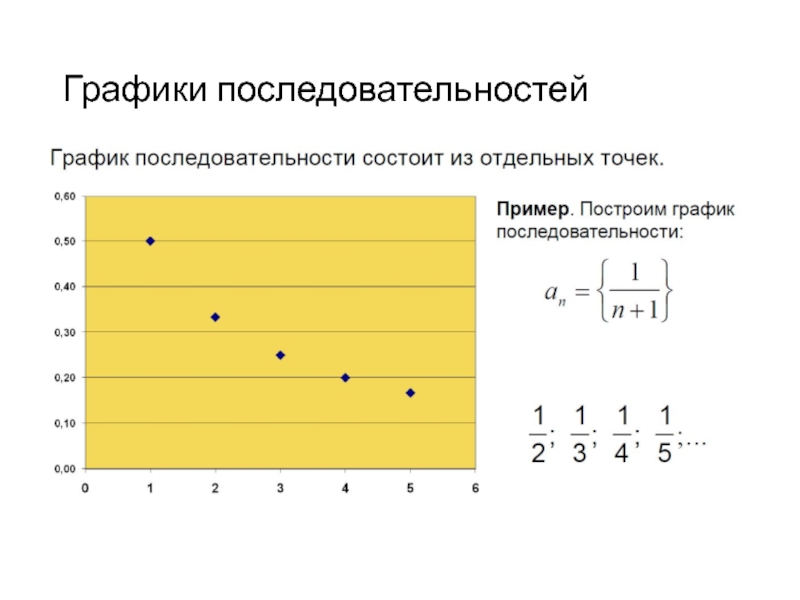
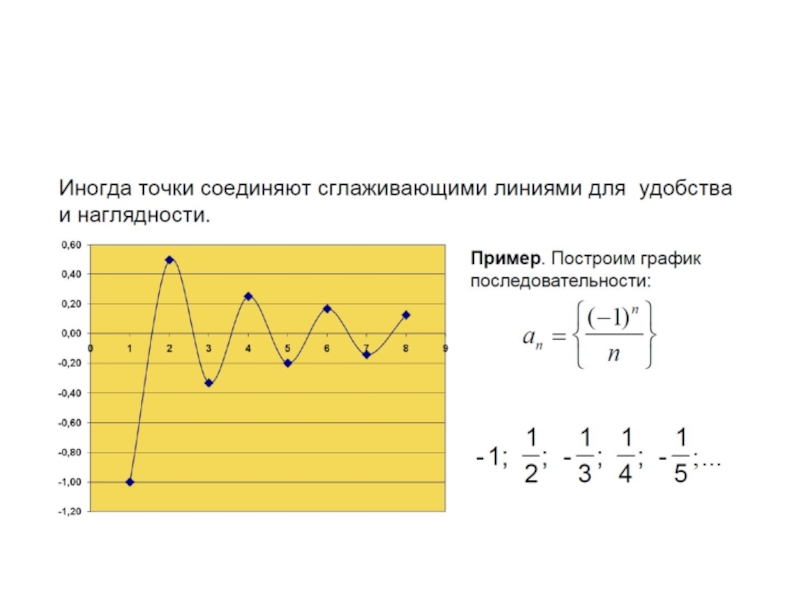
- 30. Графики последовательностей
- 32. Ограниченная последовательность
- 33. ПРИМЕРЫ
- 34. Пример ограниченной последовательности
- 36. 4-2 Предел последовательности Понятие последовательности Определение предела последовательности Геометрический смысл
- 37. Предел последовательности
- 38. Предел числовой последовательности
- 39. Определение предела в кванторах
- 41. Геометрический смысл
- 42. пример 1
- 43. решение примера 1
- 44. решение примера 1(продолжение)
- 45. пример 2
- 48. пример 3
- 49. Кому нужен такой «формализм»?
- 50. Ответ
- 51. 4-3 Основные теоремы о пределах Единственность предела Предел суммы, произведения, частного Признаки существования предела
- 52. Единственность предела
- 53. Предел суммы
- 54. Пределы произведения и частного
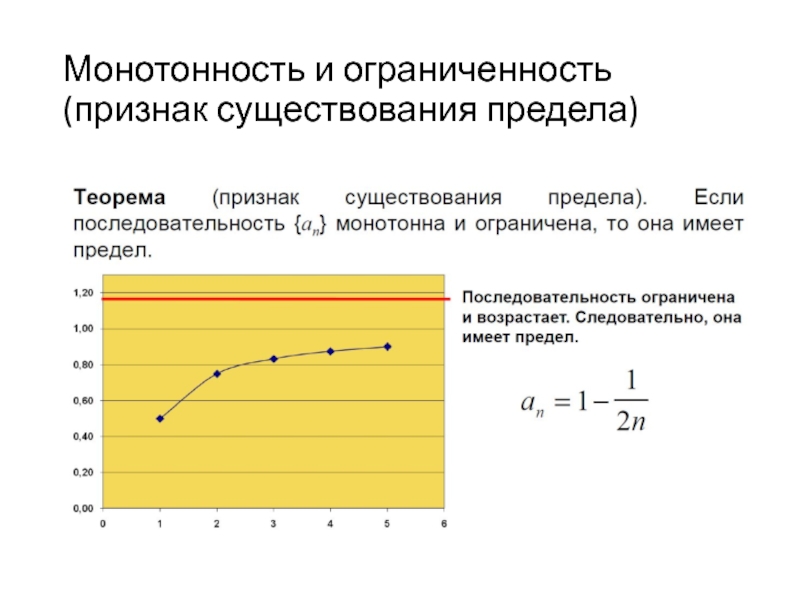
- 55. Монотонность и ограниченность (признак существования предела)
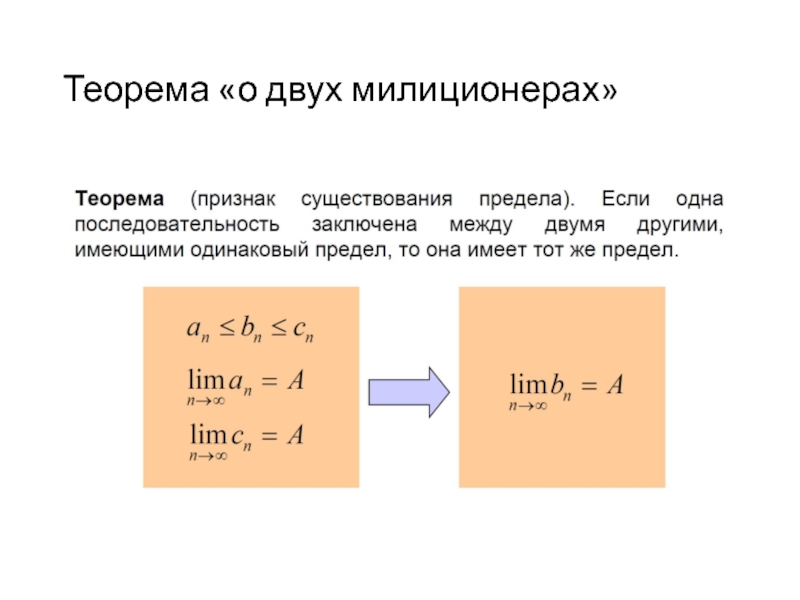
- 56. Теорема «о двух милиционерах»
- 57. 4-4 Бесконечно большие и бесконечно малые последовательности
- 60. Свойства бесконечно малых последовательностей
- 62. Примеры бесконечно малых последовательностей
- 63. 4-5 Вычисление пределов
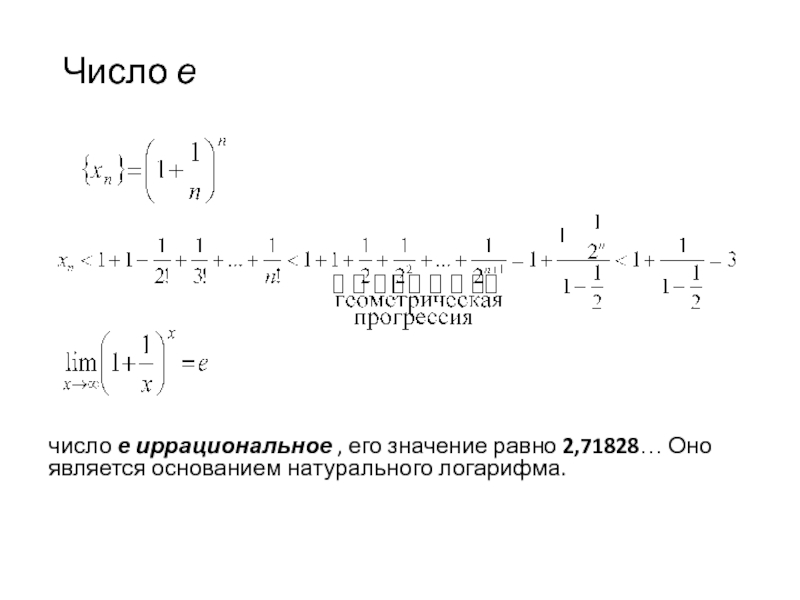
- 64. Число е
Слайд 1Математический анализ
Математический анализ не менее всеобъемлющ, чем сама природа.
Ж.Фурье
Множества.
Числовые последовательности
Слайд 31 Понятие множества
Множество (set) – некоторая, вполне определенная совокупность объектов произвольной
Георг Кантор (1845-1918)
Множество есть «объединение в одно целое объектов, хорошо различимых нашей интуицией или мыслью».
Слайд 5Объекты, которые образуют множество, называются его элементами.
Бесконечное множество содержит бесконечное число
Пример.
Множество натуральных чисел – бесконечное множество.
Множество студентов факультета – конечное множество.
Элементы множества
(set members)
Слайд 6Обозначения
В дальнейшем множества будем обозначать прописными латинскими буквами, элементы – строчными
a ∈ A – «элемент a принадлежит множеству A».
a ∉ A – «элемент a не принадлежит множеству A»
Слайд 7Множество, не содержащее ни одного элемента, называется пустым и обозначается ∅.
Пример.
Пустое множество
(empty set, null set)
Слайд 8Множество B называется подмножеством множества A, если каждый элемент множества В
Рис. Диаграмма Эйлера-Венна, изображающая подмножество В множества А
Пример. Множество первокурсников есть подмножество множества студентов.
Подмножество (subset)
Слайд 9Два множества А и В называются равными, если они состоят из
Обозначение: A = B
Например, A = {филателисты} и B={аквалангисты}
Равные множества (equal sets)
А=В ⇔ если любой филателист является одновременно аквалангистом и наоборот.
Слайд 10Универсальное множество U есть совокупность всех рассматриваемых в задаче множеств.
Пример. Имеются
A = { 3, 7, 11, 15 }
B = { 2, 4, 6, …, 2n, … }
Множество U = { все целые числа } является универсальным множеством для множеств A и B.
Универсальное множество (universal set)
Слайд 11Числовые множества
N ={1, 2, 3…} – множество натуральных чисел;
Z ={0, ±1,
Q – множество рациональных чисел вида
I – множество иррациональных чисел, т.е. чисел, представимых в виде бесконечной десятичной непериодической дроби, например , e, π, …;
R – множество действительных (вещественных) чисел, образуемое совокупностью рациональных Q и иррациональных I чисел:
Слайд 122 Операции над множествами
2-1 Объединение (сумма)
2-2 Пересечение (произведение)
2-3 Разность (вычитание)
2-4 Симметрическая
2-5 Дополнение
2-6 Свойства операций
Слайд 13Объединением (суммой) двух множеств А и В называется множество С, состоящее
2-1 Объединение множеств
(sum of sets)
Обозначение: А + В = А∪ В
ВОПРОС:
D = { 1, 3, 5} и F = { 2, 4, 6}.
Тогда M = D∪ F = ?
Пример.
A = { жители Москвы } и B = { жители Подмосковья }
С = А∪ В = { жители Москвы или Подмосковья }
Слайд 14Пересечением (произведением) двух множеств А и В называется множество D, состоящее
2-2 Пересечение множеств (intersections of sets)
Пример.
A = { студенты, участвовавшие в концерте }
B = { студенты 104 группы }
D = { студенты 104 группы, участвовавшие в концерте }
Обозначение: А·В = А∩ В
ЗАДАЧА
A = (0;5) и B = [4;9)
D = А∩В?
Слайд 15Разностью двух множеств А и В называется множество F, состоящее из
Обозначение: А – В = А \ В
2-3 Разность множеств
(set difference)
Пример.
A = [1;3] и B = N
F = А – В = (1;2)∪(2;3)
ЗАДАЧА
A = R и B = I
F = А \ I = ?
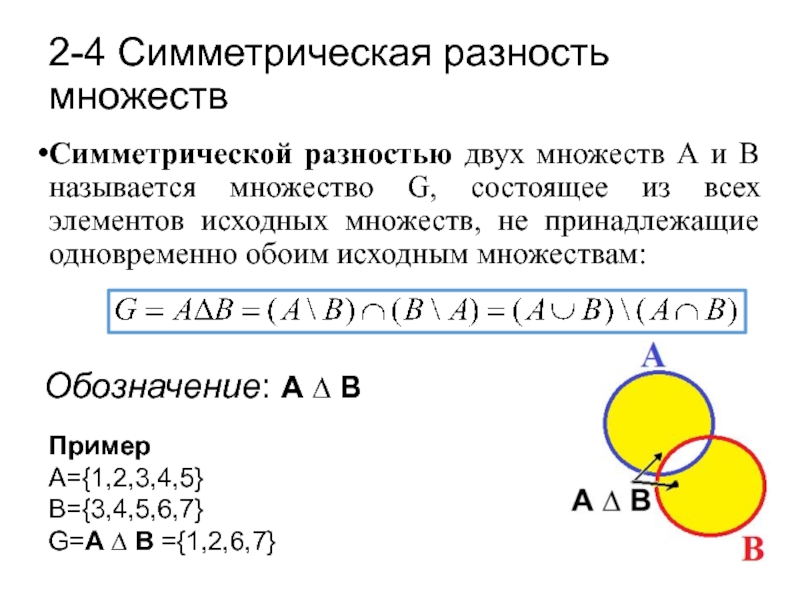
Слайд 16Симметрической разностью двух множеств А и В называется множество G, состоящее
Обозначение: А ∆ В
2-4 Симметрическая разность множеств
Пример
А={1,2,3,4,5}
B={3,4,5,6,7}
G=А ∆ В ={1,2,6,7}
Слайд 17Дополнением к множеству A называется множество элементов универсального множества, не принадлежащих
Ᾱ = U – A
Обозначение:
Пример.
A = { девушки 11 группы }
U = { все студенты 11 группы }
Ᾱ = { юноши 11 группы }
2-5 Дополнение к множеству
(set compliment)
Слайд 21Окрестность точки
(neighborhood of point)
Абсолютная величина разности двух чисел |x –
Окрестность точки c – произвольный интервал (a,b), содержащий точку с.
Слайд 24Если множество Х ограничено сверху, то говорят, что множество имеет верхнюю
Наименьшая из верхних границ множества Х называется точной верхней гранью и обозначается supX.
Наибольшая из нижних границ множества Х называется точной нижней гранью и обозначается infX.
Грани числовых множеств
Слайд 25Задача.
Найти точную верхнюю и точную нижнюю грани множества [0, 1).
Решение.
1. Это
такой, что
Множество верхних граней для данного полуинтервала [0, 1) – это множество
с наименьшим элементом, равным 1. Отсюда
причем 1 не принадлежит заданному множеству.
Слайд 26С другой стороны, наименьший элемент для рассматриваемого множества
Множество нижних граней – это множество
с наибольшим элементом, равным 0, который и является точной нижней гранью полуинтервала
Таким образом,
причем
Неограниченные множества: (-∞,∞), (-∞,2], [-5,∞).
ТВГ (-∞,2] равна 2, ТНГ [-5,∞) равна -5.
Слайд 274
Числовые последовательности
1 Определение последовательности
2 Предел последовательности
3 Теоремы о пределах
4 Бесконечно большие
5 Вычисление пределов
Слайд 284-1 Определение последовательности
Если каждому натуральному числу n по определенному закону поставлено
пронумерованных чисел x1, x2, x3,… называется числовой последовательностью.
Элементы этого множества называются членами числовой последовательности.