- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математический анализ презентация
Содержание
- 1. Математический анализ
- 2. Понятие числовой функции Переменной величиной
- 3. Если каждому числу x ставится в соответствие
- 8. Замечание: Разность двух функций бесконечно больших при
- 9. Замечательные пределы
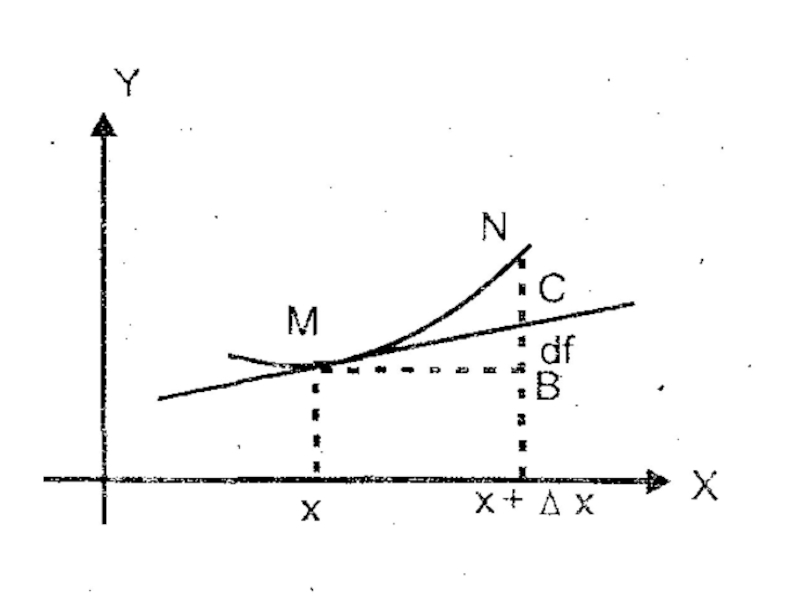
- 12. у f(x0 +Δx) f(x0 α
- 13. Пусть f(x) определена на некотором промежутке (a,
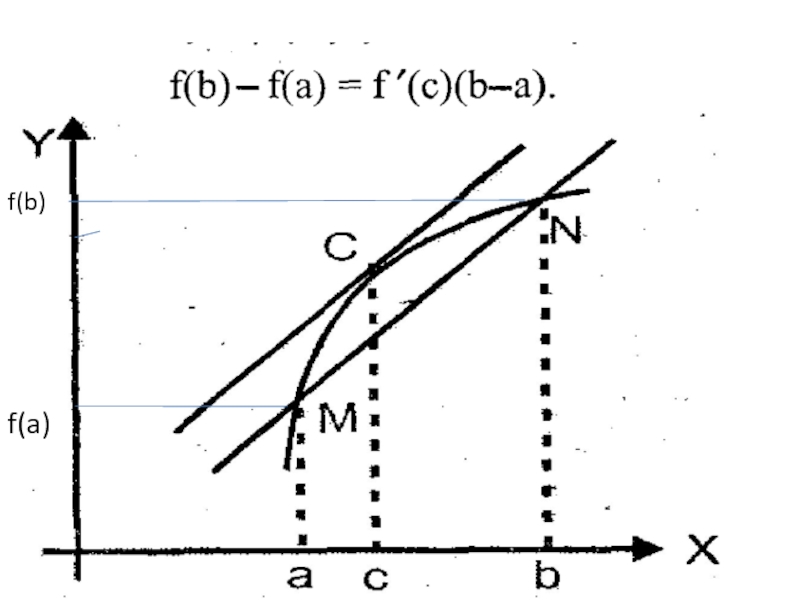
- 14. f(b) f(a)
- 18. Пример. Найти производную функции . Сначала преобразуем данную функцию:
- 22. Интегральное исчисление. Первообразная функция. Функция F(x)
- 23. Неопределенный интеграл. Определение: Неопределенным интегралом функции
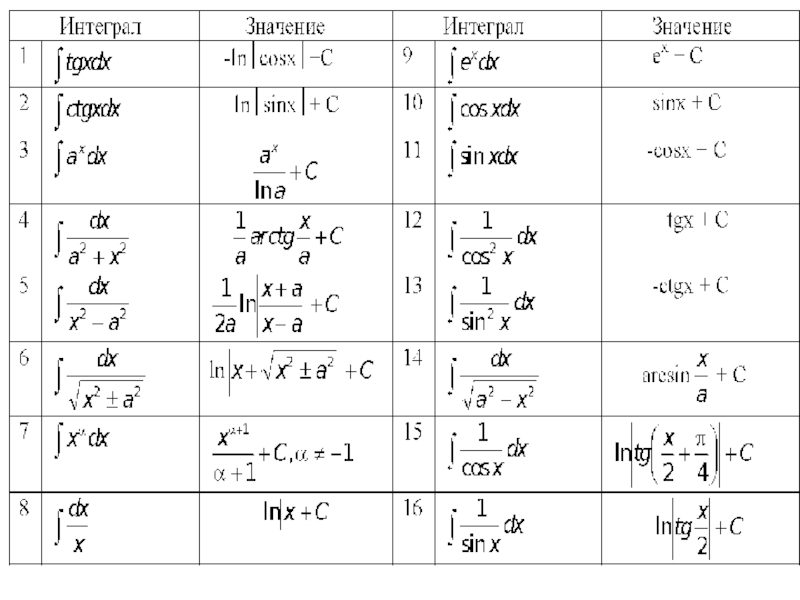
- 26. Методы интегрирования Непосредственное интегрирование.
- 27. Способ подстановки (замены переменных).
- 28. Интегрирование по частям.
- 30. Определенный интеграл. Пусть на отрезке [a, b] задана непрерывная функция f(x).
- 31. Если для функции f(x)
- 32. Свойства определенного интеграла. Если
Слайд 2 Понятие числовой функции
Переменной величиной будем называть числовую величину, которая
в изучаемой задаче принимает различные значения. Величина, принимающая только одно значение, есть частный случай переменной. Ее называют постоянной величиной или константой.
Если в изучаемой задаче несколько переменных, то различают зависимые и независимые переменные. Таковыми переменные являются лишь по отношению друг к другу, и их различие определяется условием задачи.
Если в изучаемой задаче несколько переменных, то различают зависимые и независимые переменные. Таковыми переменные являются лишь по отношению друг к другу, и их различие определяется условием задачи.
Слайд 3Если каждому числу x ставится в соответствие одно, определенное по правилу
f, число – значение числовой переменной y, то говорят, что на множестве X задана однозначная функция, или просто функция, и пишут y=f(x) x ∈ X.
Переменную x называют аргументом, множество X – областью определения функции .
Множество всех значений переменной y, поставленных в соответствие значениям аргумента x из множества X, называют множеством значений функции y = f(x). Обозначим его буквой Y.
Функция y=f(x) полностью определена, если известна область ее определения X и для каждого значения аргумента x из области определения X известно соответствующее ему значение y или известно правило f, по которому может быть найдено это значение.
Переменную x называют аргументом, множество X – областью определения функции .
Множество всех значений переменной y, поставленных в соответствие значениям аргумента x из множества X, называют множеством значений функции y = f(x). Обозначим его буквой Y.
Функция y=f(x) полностью определена, если известна область ее определения X и для каждого значения аргумента x из области определения X известно соответствующее ему значение y или известно правило f, по которому может быть найдено это значение.
Слайд 8Замечание: Разность двух функций бесконечно больших при x → a ,имеющих
значения одинаковых знаков, неопределена; неопределены также частное двух бесконечно больших функций, частное двух бесконечно малых функций, произведение бесконечно малой и бесконечно большой функций. В этом случае говорят о неопределенностях вида:
.
Для нахождения предела выражения следует раскрыть соответствующую неопределенность.
.
Для нахождения предела выражения следует раскрыть соответствующую неопределенность.
Слайд 13Пусть f(x) определена на некотором промежутке (a, b). Тогда тангенс
угла наклона секущей МР к графику функции.
где α - угол наклона касательной к графику функции f(x) в точке (x0, f(x0)).
Слайд 22Интегральное исчисление.
Первообразная функция.
Функция F(x) называется первообразной функцией функции f(x) на отрезке
[a, b], если в любой точке этого отрезка верно равенство:
F′(x) = f(x).
Надо отметить, что первообразных для одной и той же функции может быть бесконечно много. Они будут отличаться друг от друга на некоторое постоянное число.
F′(x) = f(x).
Надо отметить, что первообразных для одной и той же функции может быть бесконечно много. Они будут отличаться друг от друга на некоторое постоянное число.
Слайд 23Неопределенный интеграл.
Определение: Неопределенным интегралом функции f(x) называется совокупность первообразных функций, которые
определены соотношением:
F(x) + C.
F(x) + C.
Слайд 31
Если для функции f(x) существует предел то функция называется интегрируемой на
отрезке [a, b].



















![Интегральное исчисление.Первообразная функция.Функция F(x) называется первообразной функцией функции f(x) на отрезке [a, b], если в](/img/tmb/2/102774/d2b796fec950a005a969a1e5493c4636-800x.jpg)






![Определенный интеграл. Пусть на отрезке [a, b] задана непрерывная функция f(x).](/img/tmb/2/102774/ad04c3f6eb79f68a4b3058af25b7f9e6-800x.jpg)
![Если для функции f(x) существует предел то функция называется интегрируемой на отрезке [a, b].](/img/tmb/2/102774/ff09233172f905f43c23cde644c7670f-800x.jpg)
![Свойства определенного интеграла.Если f(x) ≤ ϕ(x) на отрезке [a, b] a < b, то](/img/tmb/2/102774/b706953e2df4ae334e2e0a2eadbce927-800x.jpg)





