- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математические утверждения и их структура. Понятия. Высказывания и предикаты. Умозаключения презентация
Содержание
- 1. Математические утверждения и их структура. Понятия. Высказывания и предикаты. Умозаключения
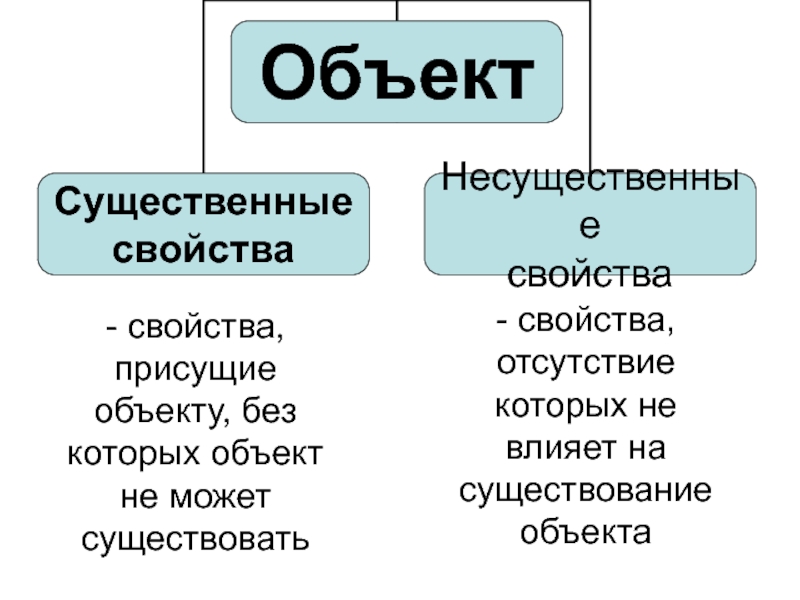
- 2. Понятия
- 3. - свойства, присущие объекту, без которых объект
- 4. Толковый словарь русского языка: Существенный – имеющий
- 5. иметь: 4 стороны 4 прямых угла равные диагонали цвет размеры расположение
- 6. В языке понятие выражается посредством слов или словосочетаний (термин)
- 8. Объем и содержание понятия Содержание понятия
- 9. Примеры: а: «прямоугольник», b:
- 10. Связь между объемом и содержанием понятия Понятия
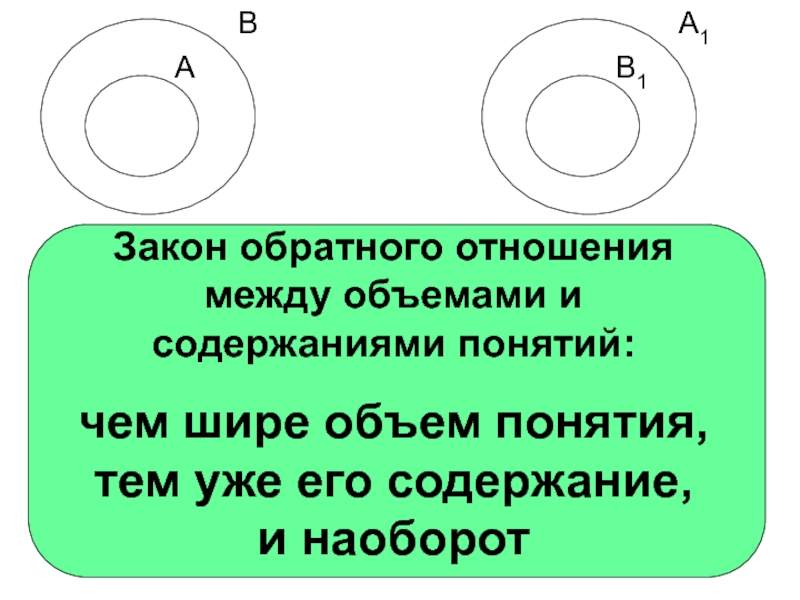
- 11. Закон обратного отношения между объемами и
- 12. Упражнения: Назовите 5 существенных свойств понятия «параллелограмм»
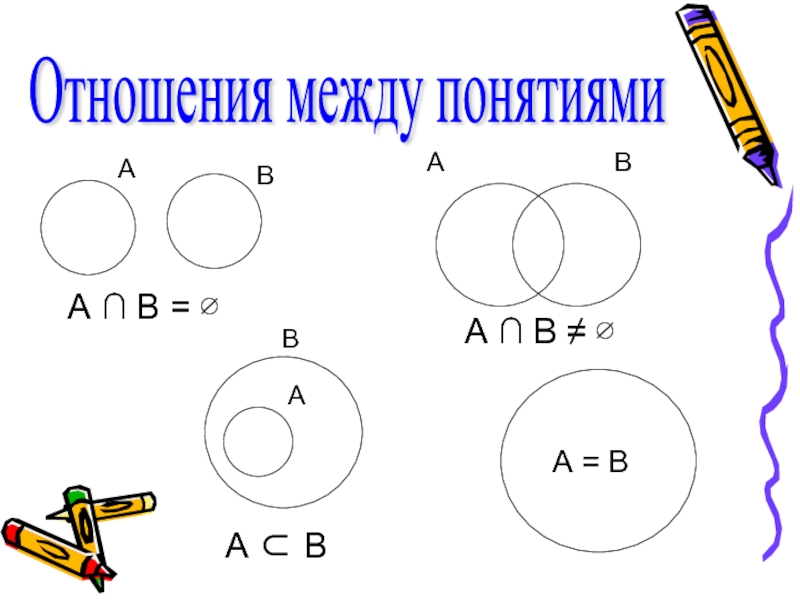
- 13. Отношения между понятиями А ∩ В
- 14. Пусть а и b – понятия, А
- 15. Если объемы понятий пересекаются, то понятия называются
- 16. Если А ⊂ В (А ≠ В),
- 17. Примеры: 1) а: «двузначное число», b: «многозначное число», 2) а: «квадрат», b: «прямоугольник», с:»четырехугольник»
- 18. Утверждения: Для данного понятия часто можно
- 19. Если объемы понятий равны, то понятия называются
- 20. Чтобы установить отношения между понятиями а и
- 21. Отношение вида и рода Отношение части и
- 22. Определение понятий
- 23. Схема определения а ⇔ b понятие, содержание
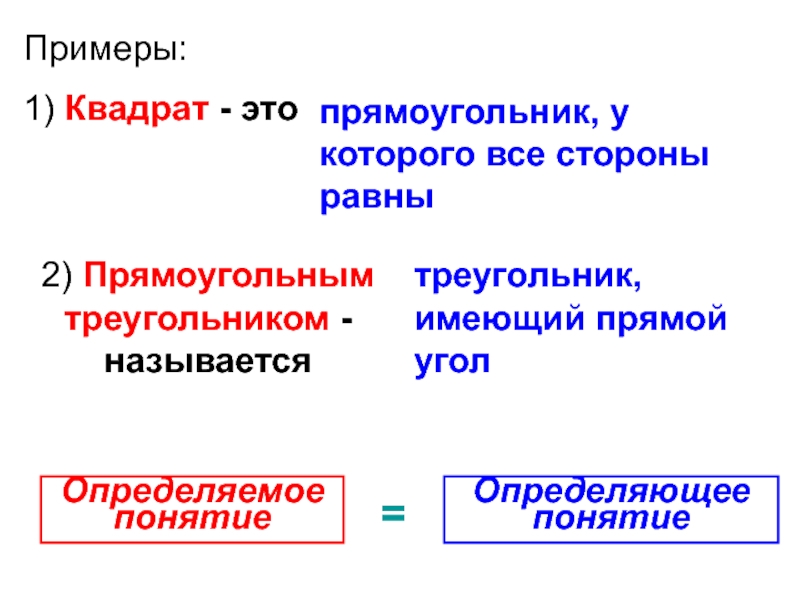
- 24. Примеры: 1) Квадрат - это прямоугольник, у
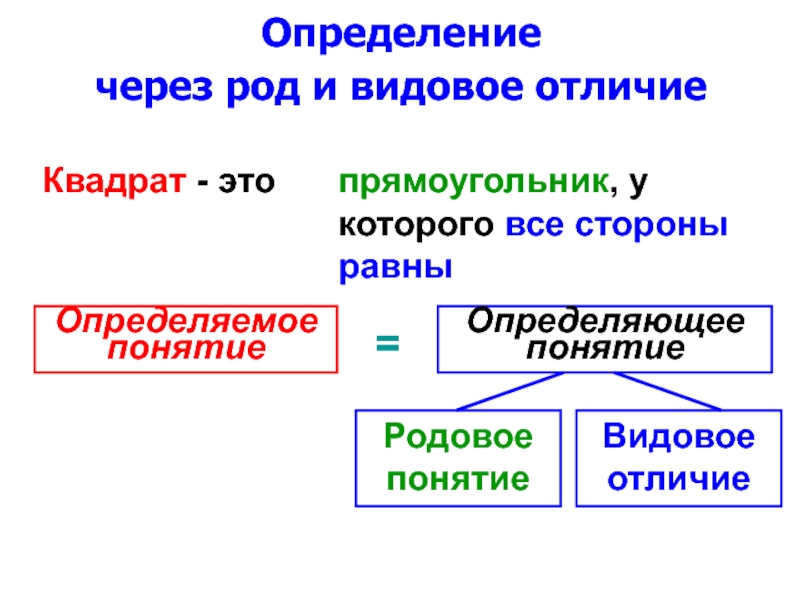
- 26. Определение через род и видовое отличие Квадрат - это прямоугольник, у которого все стороны равны
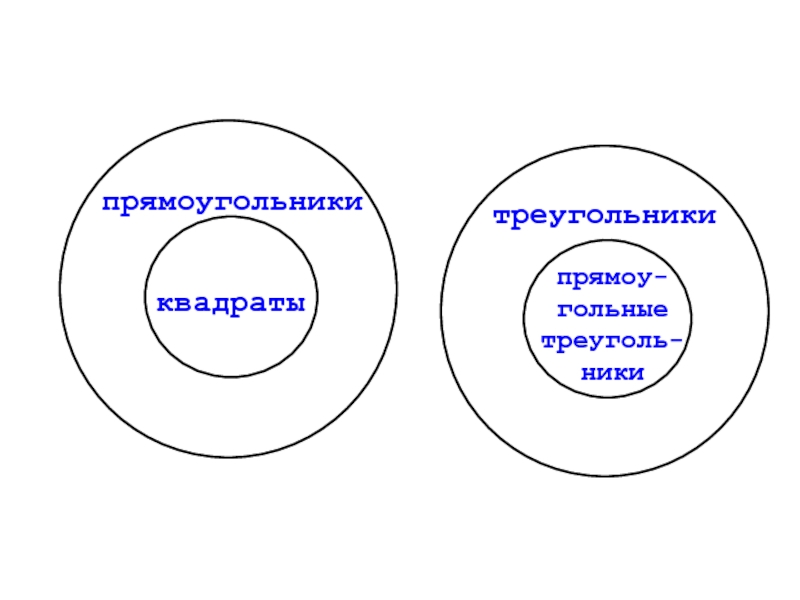
- 27. прямоугольники квадраты треугольники прямоу- гольные треуголь- ники
- 28. В любом определении понятия есть элемент произвола:
- 29. Генетическое определение (от слова «генезис» –
- 30. Примеры: Треугольником называется фигура, которая состоит
- 31. Генетическое определение
- 32. Требования к определению Соразмерность Отсутствие круга Четкость, ясность
- 33. Определение должно быть соразмерным, то есть объемы
- 34. 2) Имя существительное – это часть речи,
- 35. 3) Из истории философии. Древнегреческий философ Платон
- 36. Определение не должно содержать круга. Круг
- 37. 2) Умножение чисел – это действие, при
- 38. Определение должно быть четким, ясным
- 39. б) в определении должны быть указаны все
- 40. в) определение не должно содержать избыточных свойств
- 41. г) определение должно содержать понятие, родовое по
- 42. д) необходимо, чтобы определяемый объект существовал Пример:
- 43. Алгоритм построения определения понятия 1. Назвать
- 44. Контекстуальное определение - определение, в
- 45. Контекстуальное определение
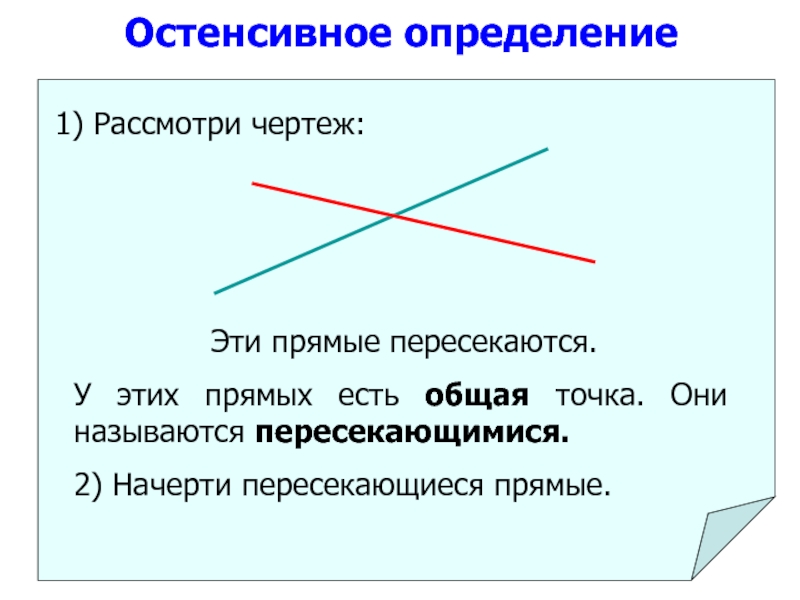
- 46. Остенсивное определение – определение путем показа.
- 47. Остенсивное определение
- 49. Упражнения 1. В следующих определениях выделите определяемое
- 50. 2. Назовите все свойства, которые содержатся в
- 51. 3. Есть ли логические ошибки в следующих
- 52. Спасибо за внимание!
Слайд 1
Математические утверждения и их структура
1. Понятия
2. Высказывания и предикаты
3. Умозаключения
Слайд 3- свойства, присущие объекту, без которых объект не может существовать
- свойства,
Слайд 4Толковый словарь русского языка:
Существенный –
имеющий большое значение, важный
Например,
существенный признак; существенные
Слайд 8Объем и содержание понятия
Содержание понятия – совокупность всех взаимосвязанных существенных
Объем понятия – совокупность всех объектов, обозначаемых одним и тем же термином
Слайд 9Примеры:
а: «прямоугольник», b: «трапеция»
А – множество прямоугольников
В –
Содержание понятия «прямоугольник»:
быть четырехугольником, иметь все прямые углы, иметь равные диагонали и др.
Содержание понятия «трапеция»:
быть четырехугольником, иметь две параллельные стороны и две непараллельные стороны.
Слайд 10Связь между объемом
и содержанием понятия
Понятия а: «квадрат», b: «прямоугольник»
Объемы А –
В – множество прямоугольников
Содержание А1 – множество существенных свойств квадрата,
В1 – множество существенных свойств прямоугольника
Слайд 11
Закон обратного отношения между объемами и содержаниями понятий:
чем шире объем
Слайд 12Упражнения:
Назовите 5 существенных свойств понятия «параллелограмм»
Каков объем понятий:
а: «однозначное натуральное
b: «натуральное число», с: «треугольник».
3. Начертите 3 геометрические фигуры, принадлежащие объему понятия «трапеция».
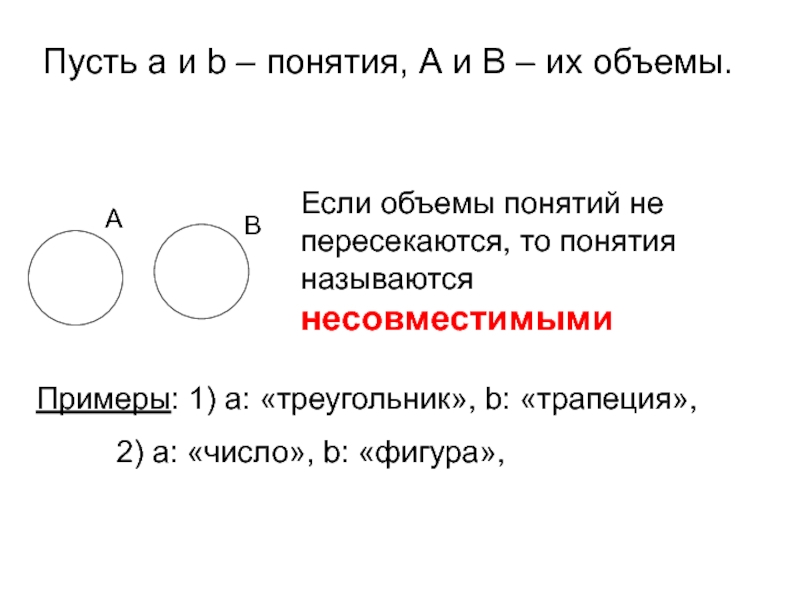
Слайд 14Пусть а и b – понятия, А и В – их
Если объемы понятий не пересекаются, то понятия называются несовместимыми
Примеры: 1) а: «треугольник», b: «трапеция»,
2) а: «число», b: «фигура»,
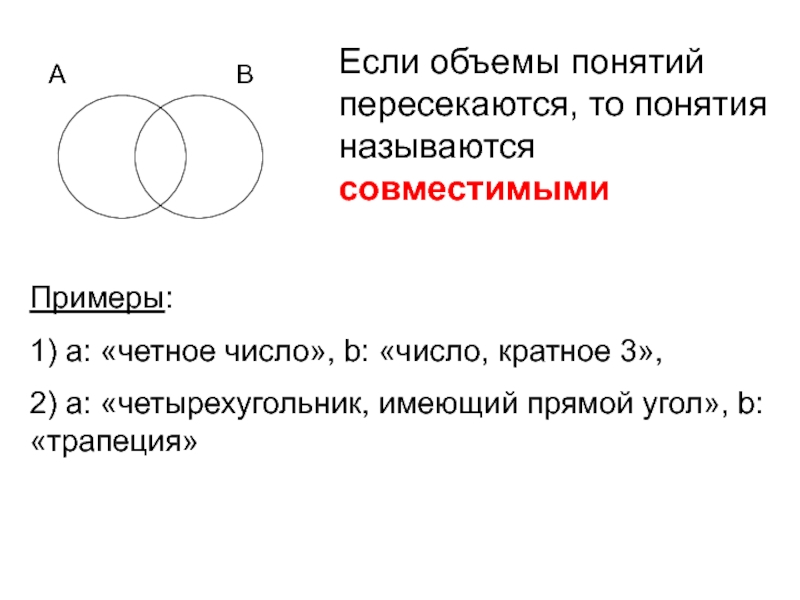
Слайд 15Если объемы понятий пересекаются, то понятия называются совместимыми
Примеры:
1) а: «четное число»,
2) а: «четырехугольник, имеющий прямой угол», b: «трапеция»
Слайд 16Если А ⊂ В (А ≠ В), то
а) понятие а
б) понятие а ỳже, чем понятие b, а понятие b шире, чем понятие а,
в) понятие а есть частный случай понятия b, а понятие b есть обобщение понятия а.
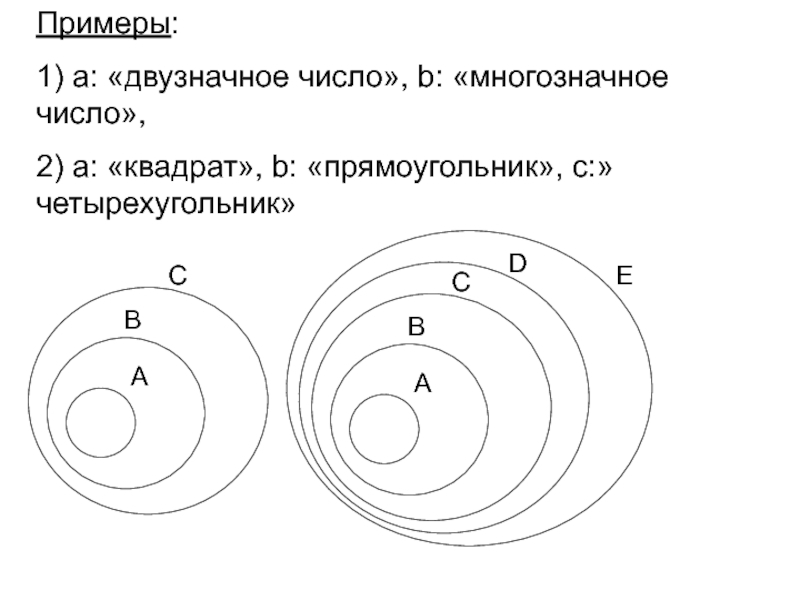
Слайд 17Примеры:
1) а: «двузначное число», b: «многозначное число»,
2) а: «квадрат», b: «прямоугольник»,
Слайд 18Утверждения:
Для данного понятия часто можно указать несколько родовых понятий.
Понятия
Слайд 19Если объемы понятий равны, то понятия называются тождественными
Примеры:
1) а: «равносторонний треугольник»,
2) а: «четное число», b: «число, кратное 2»
Слайд 20Чтобы установить отношения между понятиями а и b нужно:
1. Найти объемы
2. Установить отношения между множествами А и В.
3. Сделать вывод об отношении между понятиями а и b.
Слайд 21Отношение вида и рода
Отношение части и целого
ромб - параллелограмм
минута - час
квадрат
треугольник - фигура
окружность - круг
угол - треугольник
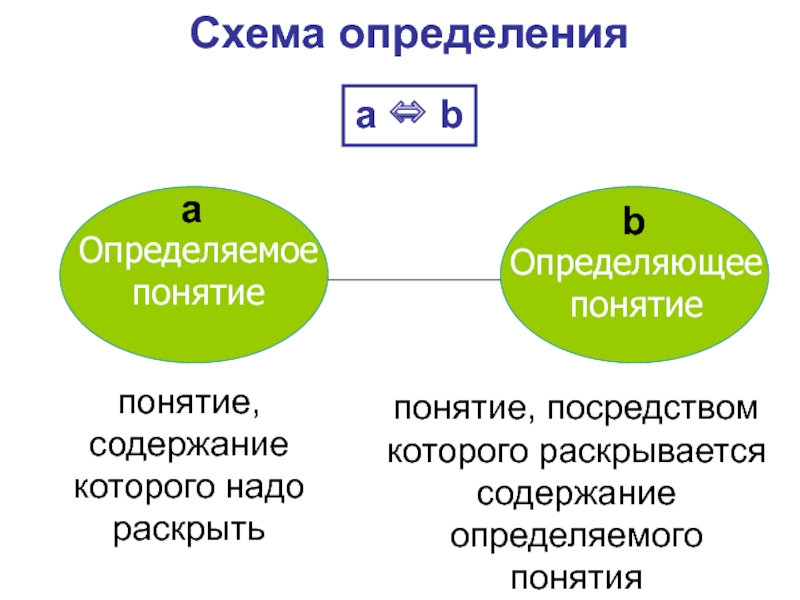
Слайд 23Схема определения
а ⇔ b
понятие, содержание которого надо раскрыть
понятие, посредством которого раскрывается
Слайд 24Примеры:
1) Квадрат - это
прямоугольник, у которого все стороны равны
2) Прямоугольным треугольником
треугольник, имеющий прямой угол
Слайд 26Определение
через род и видовое отличие
Квадрат - это
прямоугольник, у которого все стороны
Слайд 28В любом определении понятия есть элемент произвола:
в выборе термина
в
Слайд 29Генетическое определение
(от слова «генезис» – происхождение)
- определение, в котором
Слайд 30Примеры:
Треугольником называется фигура, которая состоит из трех точек, не лежащих
Шар – это геометрическая фигура, получаемая в результате вращения полукруга вокруг диаметра
Слайд 33Определение должно быть соразмерным, то есть объемы определяемого и определяющего понятий
Примеры:
1) Квадратом называется четырехугольник, у которого все стороны равны
А1 – множество квадратов,
А2 – множество четырехугольников, все стороны которых равны, т.е. множество ромбов
А1 ≠ А2 ⇒ определение несоразмерно
А1 ⊂ А2, т. е. определяющее понятие шире ⇒ ошибка широкого определения
Слайд 342) Имя существительное – это часть речи, обозначающая предмет и отвечающая
А1 – множество имен существительных,
А2 – множество частей речи, обозначающих предмет и отвечающих на вопрос «кто?»
А1 ≠ А2 ⇒ определение несоразмерно
А2 ⊂ А1, т. е. определяющее понятие уже ⇒ ошибка узкого определения
Слайд 353) Из истории философии.
Древнегреческий философ Платон дал такое определение понятия «человек»:
Другой философ Диоген с целью доказать логическую ошибку Платона в определении понятия принес на его лекцию ощипанного петуха и выпустил его в аудиторию со словами: «Вот человек Платона» Утверждают, что Платон признал свою ошибку и уточнил первоначальное определение: «Человек – это двуногое животное без перьев с широкими ногтями»
Слайд 36Определение не должно содержать круга.
Круг возникает тогда, когда определяемое и
Примеры:
1) Касательная к окружности – это прямая, которая касается окружности.
Правильно:
Касательная к окружности – это прямая, имеющая с окружностью только одну общую точку.
Слайд 372) Умножение чисел – это действие, при помощи которого находят произведение
Правильно:
Произведением натуральных чисел а и b называется натуральное число а · b, равное сумме b слагаемых, каждое из которых равно а.
Слайд 38Определение должно быть
четким, ясным
Это значит:
а) значения терминов, входящих в
Слайд 39б) в определении должны быть указаны все свойства, позволяющие однозначно выделять
Пример: Смежными называются углы, которые в сумме составляют 180о.
Правильно:
Смежные углы – это углы, одна сторона которых общая, а две другие являются дополнительными лучами
Слайд 40в) определение не должно содержать избыточных свойств в определяющей части
Пример: Прямоугольником
Правильно:
Прямоугольник - это четырехугольник, у которого все углы прямые.
Слайд 41г) определение должно содержать понятие, родовое по отношению к определяемому. При
Пример: Квадрат – это когда все стороны равны.
Правильно: Квадрат - это прямоугольник, у которого все стороны равны.
Квадрат – это четырехугольник, у которого все стороны равны и все углы прямые.
Слайд 42д) необходимо, чтобы определяемый объект существовал
Пример: Тупоугольный треугольник – это треугольник,
Правильно:
Тупоугольный треугольник - это треугольник, имеющий тупой угол.
Слайд 43Алгоритм построения определения понятия
1. Назвать определяемое понятие (термин).
2. Указать ближайшее родовое
3. Сформулировать видовое отличие, т.е. перечислить свойства, выделяющие определяемые объекты из объема родового понятия.
4. Проверить, выполнены ли требования к определению понятия (соразмерность, отсутствие круга, ясность).
Слайд 44Контекстуальное определение
- определение, в котором содержание нового понятия раскрывается
Слайд 49Упражнения
1. В следующих определениях выделите определяемое и определяющее понятия, родовое понятие
1) Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.
2) Отрезок, соединяющий середины двух сторон треугольника, называется его средней линией.
Слайд 502. Назовите все свойства, которые содержатся в видовом отличии каждого из
1) Биссектрисой угла называется луч, выходящий из вершины угла делящий угол пополам.
2) Прямые называются параллельными, если они лежат в одной плоскости и не пересекаются.
Слайд 513. Есть ли логические ошибки в следующих определениях? Если можете, исправьте
1) Прямоугольником называется четырехугольник, у которого противоположные стороны равны.
2) Биссектрисой угла называется прямая, делящая угол пополам.
3) Сложением называется действие, при котором числа складываются.
4) Равносторонним треугольником называется треугольник, у которого равны все стороны и все углы.
5) Параллелограммом называется многоугольник, у которого противоположные стороны попарно параллельны