Тема:
«МАТЕМАТИЧЕСКИЕ ПРЕДЛОЖЕНИЯ»
Выполнил: Цырендашиева Э.Б.-Ц.
Проверил: Астапова Н.И.
г. Улан-Удэ
2007 год
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математические предложения презентация
Содержание
- 1. Математические предложения
- 2. План: Высказывания Высказывательная форма Конъюнкция высказываний Конъюнкция
- 3. Высказывание в математике называют предложение, относительно которого
- 4. Высказывательная форма предложение с переменной, которое обращается
- 5. Для выявления логической структуры составного предложения нужно
- 6. Конъюнкцией высказываний А и В (смысл союза
- 7. Используя данное определение, найдем значение истинности высказывания
- 8. Конъюнкция одноместных высказывательных форм А(х) и В(х),
- 9. Докажем это равенство. Пусть а – произвольный
- 10. Дизъюнкция высказываний А и В (смысл союза
- 11. Используя данное определение, найдем
- 12. Дизъюнкцию одноместных высказывательных форм А(х) и В(х),
- 13. Решение задач на распознавание объектов. В задачах
- 14. Решают такие задачи, используя определение соответствующего понятия.
- 15. Поэтому распознавание производиться по следующему правилу: Проверяем,
- 16. Выясним какие из фигур на рисунке являются
- 17. Если видовое отличие представляет собой конъюнкцию свойств,
- 18. Высказывания с кванторами Cлова «все» и «некоторые»
- 19. Различают кванторы общности и существования. Кванторы общности
- 20. Таким образом, если перед одноместной высказывательной
- 21. Как устанавливают значение истинности высказываний с квантором?
- 22. Выясним, как устанавливают значение истинности высказывания с
- 23. Истинность высказываний с квантором общности Устанавливается путем
- 24. Отрицание высказываний А называется высказывание А, которое
- 25. Отрицанием конъюнкции двух высказываний А и В
- 27. Про высказывания вида А^В и АvВ говорят,
- 28. Как быть с высказываниями, которые содержат кванторы?
- 29. Вообще если дано предложение ( x)А(х), то
- 30. Получаем две равносильности:
- 31. Отрицание высказывательных форм Пусть на множестве Х
- 32. Отношение следования между предложениями Высказывательная форма В(х)
- 33. Для обозначения отношения логического следования используется знак
- 34. Как и любое высказывание, предложение А(х)
- 35. Отношение равносильности между предложениями Предложения А(х) и
- 36. Для обозначения отношения равносильности используется знак
- 37. Заметим, что мы рассматриваем понятия логического следования
- 38. Структура теорем. Теорема – это высказывание,
- 39. Условием теоремы «если четырехугольник является прямоугольником, то
- 40. Виды теорем Пусть дана теорема А
- 41. Пример. Дана теорема: «Если углы вертикальные, то
- 42. Существует ли какая-нибудь связь между названными видами
- 43. После того, как доказана какая-либо теорема вида
- 44. Спасибо за внимание!
Слайд 1Министерство образования и науки республики Бурятия Государственное образовательное учреждение Среднего профессионального
Слайд 2План:
Высказывания
Высказывательная форма
Конъюнкция высказываний
Конъюнкция высказывательных форм
Дизъюнкция высказываний
Дизъюнкция высказывательных форм
Решение задач на распознавание
Высказывания с кванторами
Отрицание высказываний
Отрицание высказывательных форм
Отношение следования между предложениями
Отношение равносильности между предложениями
Структура теоремы. Виды теорем
Слайд 3Высказывание
в математике называют предложение, относительно которого
имеет смысл вопрос: истинно оно или
принято обозначать прописными буквами латинского
алфавита: А,В,С,…,Z.
Высказывания
истинные – «И» ложные – «Л»
1.Некоторые числа делятся на 3 1. 2 + 5 > 8
2.Число 12 – четное. 2. Число 25 - четное
«Истина» и «ложь» называются значениями истинности
высказывания. Каждое высказывание либо истинно, либо
ложно, быть одновременно тем и другим оно не может.
Слайд 4Высказывательная форма
предложение с переменной, которое обращается в
высказывание при подстановке в него
из множества Х.
Высказывательная форма
элементарные составные
Число 14 делится на 4 Число 14 не делится на 4
Составные предложения образуются из элементарных с
помощью слов «И», «ИЛИ», «ЕСЛИ …, ТО…», «ТОГДА И
ТОЛЬКО ТОГДА, КОГДА», частицы «НЕ». Эти слова в
математике называют логическими связками.
Слайд 5Для выявления логической структуры составного предложения нужно
установить:
Из каких элементарных предложений образовано
С помощью каких логических связок оно образовано.
Логическая структура предложения «Если углы
вертикальные, то они равны». Оно состоит из двух
элементарных предложений: предложения А – «углы
вертикальные» и предложения В – «углы равны».
Соединены они в одно составное предложение с
помощью логической связки «если …, то…». Говорят,
что данное составное предложение имеет логическую
структуру (форму): «если А, то В».
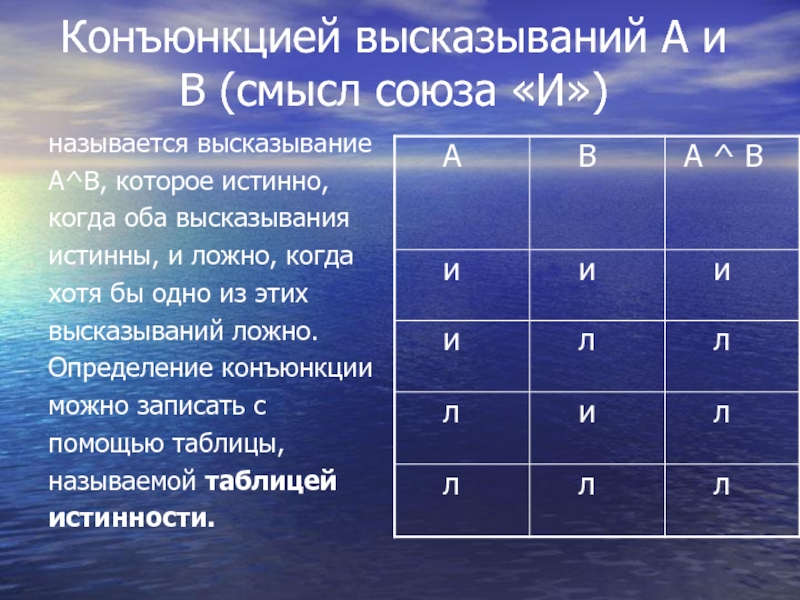
Слайд 6Конъюнкцией высказываний А и В (смысл союза «И»)
называется высказывание
А^В, которое истинно,
когда
истинны, и ложно, когда
хотя бы одно из этих
высказываний ложно.
Определение конъюнкции
можно записать с
помощью таблицы,
называемой таблицей
истинности.
Слайд 7 Используя данное определение, найдем значение
истинности высказывания «число 28 делится на 7
9», которое как было установлено раньше, состоит
из двух элементарных высказываний, соединенных
союзом «И», т. е. является конъюнкцией. Так как
первое высказывание истинно, а второе ложно, то,
согласно определению конъюнкции, высказывание
«число 28 делится на 7 и на 9» будет ложным.
В обыденной речи конъюнкция может выражаться
не только с помощью союза «И», но и другими
например, «А», «НО», «ОДНАКО», «НЕ ТОЛЬКО …,
НО И …». Например: «Число 15 делится не только
на 3, но и на 5».
Слайд 8 Конъюнкция одноместных высказывательных форм
А(х) и В(х), заданных на множестве Х, обозначают
А(х)
области определения Х высказывательная форма
А(х) В(х) обращается в истинное высказывание?
Очевидно что это возможно при тех и только тех
значениях х, при которых обращаются в истинное
высказывание обе высказывательные формы А(х) и
В(х). Если обозначить ТА – множество истинности
предложения А(х), ТВ – множество истинности
предложения В(х), а множество истинности их
конъюнкции ТА^В, то, по всей видимости,
ТА^B =ТА ТВ.
Слайд 9Докажем это равенство.
Пусть а – произвольный элемент множества Х и известно,
Докажем обратное утверждение. Пусть а – произвольный элемент множества Х и известно, что
а ТА ТВ. По определению пересечения множеств это означает, что а ТА и а ТВ, откуда получаем, что А(а) и В(а) – истинные высказывания, поэтому конъюнкция высказываний А(а) В(а) также будет истинна. А это означает, что элемент а принадлежит множеству истинности высказывательной формы А(х) В(х), т.е.
а ТА^В. Таким образом, мы доказали, что ТА ТВ ТА^В.
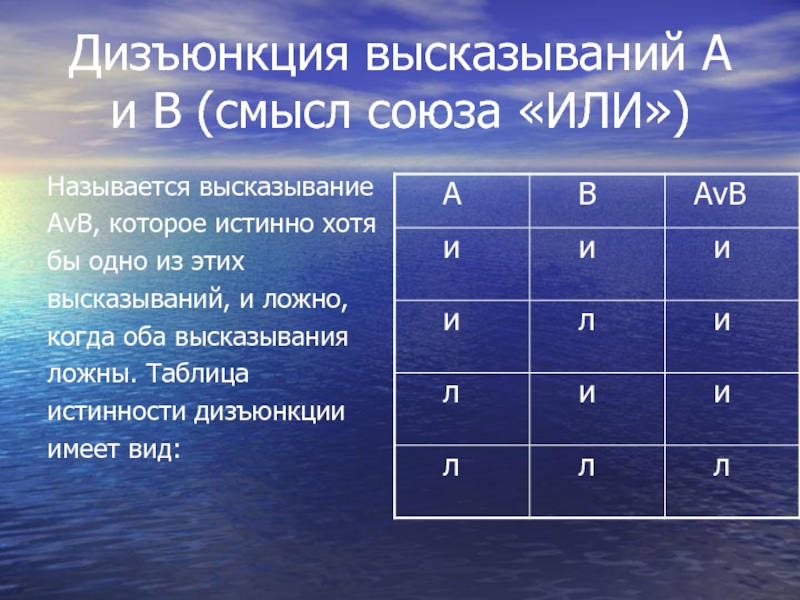
Слайд 10Дизъюнкция высказываний А и В (смысл союза «ИЛИ»)
Называется высказывание
АvВ, которое
бы одно из этих
высказываний, и ложно,
когда оба высказывания
ложны. Таблица
истинности дизъюнкции
имеет вид:
Слайд 11 Используя данное определение, найдем
значение истинности высказывания «число 28
делится
является дизъюнкцией двух высказываний, одно
из которых истинно, то, согласно определению оно
истинно.
Из определения дизъюнкции следует, что в
математике союз «ИЛИ» используется как не
неразделительный, т.е. допускается возможность
одновременного выполнения обоих условий. Так,
высказывание «15 кратно 3 или 5», согласно
определению, считается истинным, поскольку оба
высказывания «15 кратно 5» истинны.
Слайд 12Дизъюнкцию одноместных высказывательных
форм А(х) и В(х), заданных на множестве Х,
обозначают А(х)vВ(х).
обращаться в истинное высказывание при тех и
только тех значениях х из области определения
Х, при которых обращается в истинное
высказывание хотя бы одна из
высказывательных форм, т.е. ТАvВ=ТА ТВ.
Доказательство этого равенства проводиться
аналогично конъюнкции.
Слайд 13Решение задач на распознавание объектов.
В задачах на распознавание требуется
ответить на вопрос:
или иной объект объему данного понятия
или не принадлежит. Примером такой
задачи может быть следующая:
«Установите, какие из фигур являются
квадратами, а какие нет».
1
3
2
Слайд 14 Решают такие задачи, используя определение
соответствующего понятия. При этом важно понимать,
что если
с и видовое отличие Р, то его объем А можно
представить в таком виде: А = {х I х C и Р(х)}
характеристическое свойство элементов,
принадлежащих объему понятия а, представляет собой
конъюнкцию двух свойств:
Принадлежности объекта х объему С родового понятия (х С);
Свойства Р(х).
Это означает, что объект х будет принадлежать объему
понятия а тогда и только тогда, когда он (этот объект)
содержится в объеме родового понятия и обладает
свойством Р.
Слайд 15Поэтому распознавание производиться по следующему правилу:
Проверяем, принадлежит ли объект х объему
Если окажется, что х С, то проверку прекращаем и делаем вывод, что объект х не принадлежит объему понятия а, т.е. х А.
Если х С, то продолжаем проверку и выясняем, обладает ли объект х свойством Р.
Если объект х обладает свойством Р, то делаем вывод о его принадлежности объему понятия а, т.е. утверждаем, что х А.
Если окажется, что объект х не обладает свойством Р, то делаем вывод, что объект х не принадлежит объему понятия а, т.е. х А.
Слайд 16 Выясним какие из фигур на рисунке являются
квадратами. Будем пользоваться таким определением:
«Квадратом
соседние стороны равны». Из него следует, что для
того, чтобы фигура была квадратом, она должна
обладать двумя свойствами: «быть прямоугольником» и
«иметь равные соседние стороны».
Фигура 1 является квадратом, так как это
прямоугольник, соседние стороны которого равны.
Фигура 2 не является квадратом, так как это не
прямоугольник.
Фигура 3 – прямоугольник, но соседние стороны в
нем не равны. Следовательно, ее нельзя назвать
квадратом.
Слайд 17 Если видовое отличие представляет собой
конъюнкцию свойств, т.е. Р=Р1 Р2 … Рn,
распознавание проводиться по следующему
правилу: проверяют поочередно наличие у
объекта каждого из свойств Р1, Р2,…,Рn; если
окажется, что он не обладает каким-либо из
этих свойств, то проверку прекращают и
делают вывод о том, что объект не обладает
свойством Р; если же окажется, что все
свойства Р1,Р2,…,Рn присущи данному объекту,
nо заключают, что объект обладает свойством
Р.
Слайд 18Высказывания с кванторами
Cлова «все» и «некоторые» называют
кванторами. Слово «квантор»
латинского происхождения и
«сколько», т.е. квантор показывает, о
скольких (всех или некоторых)
объектах говориться в том или ином
предложении.
Слайд 19 Различают кванторы общности и
существования.
Кванторы общности – это слова
«любой», «всякий», «каждый»,
«все».
Кванторы
слова «существует»,«некоторые»,
«найдется», «хотя бы один».
Слайд 20 Таким образом, если перед одноместной
высказывательной формой поставить
какой-либо квантор, то получаем
высказывание.
одноместной высказывательной формы
высказывание можно не только
подставляя в нее конкретные значения
переменной, но и поставив перед
высказывательной формой квантор
(общности или существования).
Слайд 21 Как устанавливают значение истинности высказываний с квантором?
Рассмотрим высказывания:
1. Любое число 0,1,…,9
2. Любой прямоугольник является квадратом.
Как устроены данные высказывания? Все они содержат квантор общности,
выраженный словом «любой». Истинны или ложны эти высказывания?
Обратимся к первому предложению. Чтобы убедиться в том, что любое из
чисел 0,1,…,9 является решением неравенства х+2>х, рассмотрим случаи:
При х=0 имеем 0+2>0, т.е. истинное числовое неравенство.
При х=1 имеем 1+2>1, т.е. истинное числовое неравенство.
…………………………………………………………………….......
При х=9 имеем 9+2>9, т.е. истинное числовое неравенство.
Действительно, любое число из совокупности 0,1,…,9 является решением
неравенства х+2>х, т.е. высказывание «Любое число 0,1,…,9 является решением
неравенства х+2>х» - истинное высказывание. Каким образом мы установили это?
Доказали, рассмотрев все частные и возможные случаи, способ доказательства,
который был использован нами, называется полной индукцией.
Рассмотрим 2-е предложение. Это – ложное высказывание. Чтобы убедиться
в этом, достаточно начертить прямоугольник, не являющийся квадратом. Мы
опровергли данное высказывание, приведя контрпример.
Слайд 22 Выясним, как устанавливают значение истинности
высказывания с квантором существования. Рассмотрим
высказывания:
1. Существуют натуральные
2. Существуют прямоугольные равносторонние треугольники.
Первое высказывание истинное. Чтобы обосновать этот
вывод, достаточно привести пример. Так, 9 – число
натуральное и делиться на 3.
Второе высказывание ложное. Действительно, в
прямоугольном треугольнике один угол обязательно
содержит 90градусов, а в равностороннем треугольнике
величина всех углов 60. Значит, среди прямоугольных
треугольников равносторонних нет.
Слайд 23 Истинность
высказываний с
квантором
общности
Устанавливается
путем доказательства.
Чтобы убедиться в
ложности таких
высказываний
(опровергнув их),
достаточно привести
контпример.
Истинность
высказывания с
квантором
существования
устанавливается
помощи конкретного
примера. Чтобы
убедиться в ложности
такого высказывания,
необходимо провести
доказательство.
Слайд 24Отрицание высказываний А
называется
высказывание А,
которое ложно, когда
высказывание А
истинно, и истинно,
когда высказывание А
–
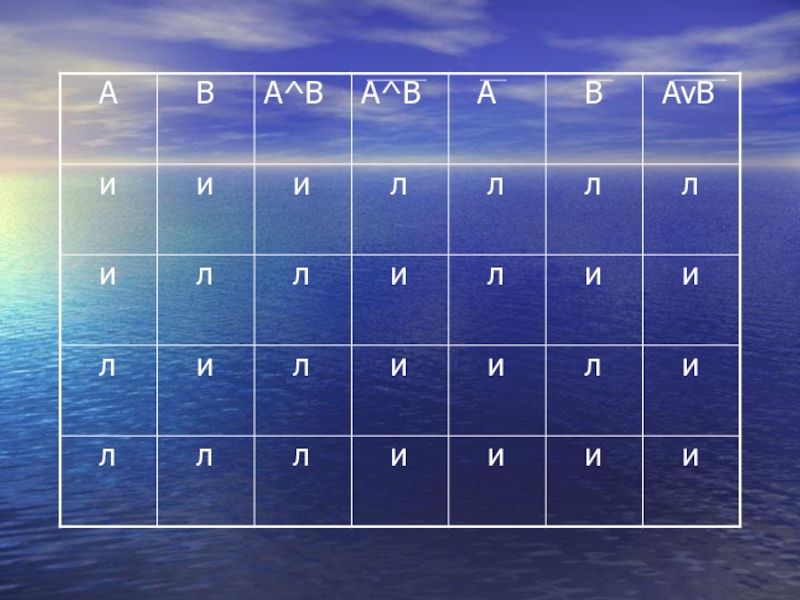
Слайд 25 Отрицанием конъюнкции двух
высказываний А и В является
дизъюнкция их отрицаний. Для этого
надо
истинности высказываний вида А^В и АvB
совпадают при любых значениях
истинности высказываний А и В. Сделать
это можно при помощи таблицы
истинности:
Слайд 27 Про высказывания вида А^В и АvВ говорят, что они
равносильны, и пишут
Аналогично можно доказать, что имеет место
равносильность АvВ А^В.
Эти равносильности носят название законов де
Моргана.
Из них вытекает следующее правило построения
отрицания конъюнкции и дизъюнкции: чтобы
построить отрицание конъюнкции (дизъюнкции),
достаточно заменить отрицаниями
составляющие ее высказывания, а союз «И»
(«ИЛИ») заменить союзом «ИЛИ» («И»).
Слайд 28 Как быть с высказываниями, которые
содержат кванторы? Достаточно ли для
отрицания таких предложений
частицу «НЕ»? Например, будет ли отрицанием
высказывания «всякий прямоугольный
треугольник является равнобедренным»
предложение «всякий прямоугольный
треугольник не является равнобедренным»?
Видим, что не будет, так как оба высказывания
ложны. Таким образом, строить отрицания
высказываний с кванторами при помощи
частицы «НЕ» перед сказуемым нельзя.
Слайд 29 Вообще если дано предложение
( x)А(х), то его отрицанием будут
предложения ( х)А(х)
один и тот же смысл (и одно и то же
значение истинности).
Если дано предложение , то его
отрицанием будут предложения и
, также имеющие один и то же
смысл (и одно и тоже значение
истинности).
Слайд 30 Получаем две равносильности:
Из них вытекает правило: для того
построить отрицание высказывания,
начинающегося с квантора общности
(существования), достаточно заменить
его квантором существования (общности)
и построить отрицание предложения,
стоящего после квантора.
Слайд 31Отрицание высказывательных форм
Пусть на множестве Х задана высказывательная
форма А(х). Ее отрицание
или «неверно, что А(х)»). Предложение А(х) будет
обращаться в истинное высказывание лишь при тех
значениях х из множества Х, при которых А(х) – ложно. Таким
образом, ТА=Т’А, где ТА – множество истинности
предложения А(х), а Т’А– дополнение множества ТА до
множества Х.
Доказательство этого равенства мы опускаем.
Пусть, например, на множестве натуральных чисел задана
высказывательная форма А(х) – «число х кратно 5». Тогда ее
отрицанием будет предложение «число х не кратно 5» (или
«неверно, что число х кратно 5»), истинное при всех
значениях х которые не кратны 5.
Слайд 32Отношение следования между предложениями
Высказывательная форма В(х) следует
из высказывательной формы А(х), если
В(х)
высказывание при всех тех значениях х,
при которых А(х) истинна.
Если А и В – высказывания, тогда
говорят, что из А следует В, если всякий
раз, когда А истинно, истинно и В.
Слайд 33 Для обозначения отношения логического
следования используется знак . Соединяя
две
таким знаком, мы получаем высказывание
А(х) В(х), прочитать которое можно по
разному:
1. Из А(х) следует В(х).
2. Всякое А(х) есть В(х).
3. Если А(х), то В(х).
4. В(х) есть следствие А(х).
5. А(х) есть достаточное условие для В(х).
6. В(х) есть необходимое условие для А(х).
Слайд 34 Как и любое высказывание, предложение
А(х) В(х) может быть истинным
так как оно не может быть сформулировано в виде
«всякое А(х) есть В(х)», то его истинность
устанавливается путем доказательства, а с
помощью контрпримера – что оно ложно. Например, для того чтобы число делилось на 5,
необходимо, чтобы его запись оканчивалась нулем.
Решение: Если сформулировать данное
высказывание в виде «из того, что число делится
на 5, следует, что его запись оканчивается нулем»,
то сразу можно сказать, что оно ложное. И
убедиться в этом можно при помощи
контрпримера. Так, число 35 делится на 5, но его
запись не оканчивается нулем.
Слайд 35Отношение равносильности между предложениями
Предложения А(х) и В(х)
равносильны, если из предложения
А(х) следует
предложения В(х) следует
предложение А(х).
Слайд 36 Для обозначения отношения равносильности
используется знак . Соединяя две
высказывательные формы
знаком, мы получаем высказывание А(х) В(х),
Прочитать которое можно по-разному:
1. А(х) равносильно В(х).
2. А(х) тогда и только тогда, когда В(х).
3. А(х) – необходимое и достаточное условие для В(х).
4. В(х) – необходимое и достаточное условие для А(х).
Слайд 37 Заметим, что мы рассматриваем понятия
логического следования и равносильности для
одноместных высказывательных форм.
предложений, содержащих две или более
переменных, эти понятия определяются аналогично.
Знак мы также использовали в записи правил
построения отрицания высказываний. Например,
А^В АvВ. В этом случае речь идет о
равносильности высказываний определенной
формы. При этом считают, что предложения
равносильны, если они одновременно истинны, либо
одновременно ложны. Другими словами,
если их значения истинности совпадают при
одинаковых наборах значений высказываний А и В.
Слайд 38Структура теорем.
Теорема – это высказывание, истинность
которого устанавливается посредством
рассуждения (доказательства).
С логической
представляет собой высказывание вида А В, где
А и В – высказывательные формы с одной или
несколькими переменными. Предложение А
называют условием теоремы, а предложение В –
ее заключением.
Слайд 39 Условием теоремы «если
четырехугольник является
прямоугольником, то в нем диагонали
равны» является предложение
«четырехугольник -
заключением – предложение «в таком
четырехугольнике диагонали равны». Однако, в каком бы виде ни была
сформулирована теорема, в ней всегда
выделяется условие А (что надо) и
заключение В (что надо доказать).
Слайд 40Виды теорем
Пусть дана теорема А В. Образуем из
нее высказывания вида
Теоремы А В и В А называются
обратными друг другу, а теоремы А В и
А В называются противоположными
друг другу.
Теорему В А называют обратной
противоположной.
Слайд 41 Пример. Дана теорема: «Если углы
вертикальные, то они равны». Сформируем
теоремы обратную,
противоположную и
Обратная данной: «Если углы равны, то они
вертикальные». Это – ложное высказывание.
Противоположная данной: «Если углы не
являются вертикальными, то они не равны». Это
тоже ложное высказывание.
Обратная противоположной: «Если углы не
равны, то они не вертикальные». Это – истинное
высказывание.
Слайд 42 Существует ли какая-нибудь связь
между названными видами теорем?
Установлено, что теоремы А
равносильны, т.е. всегда, когда истинна
теорема А В, будет истинна и теорема В
А, и наоборот:
А В В А
Полученную равносильность называют
законом контрапозиции.
Слайд 43 После того, как доказана какая-либо теорема
вида А В, имеет смысл
ей теорему. В каждом случае нужно проводить
ее самостоятельное доказательство, так как
теорема, обратная данной, может быть ложной.
Так случилось, например, в рассмотренном
выше примере.
Если окажутся верными и данная теорема и
ей обратная, то можно их объединить в одну с
помощью слов «тогда и только тогда, когда»
или «необходимо и достаточно».