- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математические модели, постановки задач, алгоритмы обучения, оценки решающих правил презентация
Содержание
- 1. Математические модели, постановки задач, алгоритмы обучения, оценки решающих правил
- 2. План лекции Классификация моделей, прямая и обратная
- 3. Математическая модель Математическая модель – математическое представление
- 4. Классификация моделей
- 5. Прямая и обратная задачи математического моделирования
- 6. Виды моделирования
- 7. Процесс моделирования Этап 1 Этап
- 8. Критерии выбора моделей и методы отбора признаков
- 10. Стандартные постановки основных задач ИФБЗ Для некоторого
- 11. Правильная и точная классификации Правильная
- 12. Отличия задач классификации и кластеризации Задача кластеризации
- 13. Компоненты формирования Индуктивная база знаний формирование
- 14. Алгоритм обучения классификации Алгоритм классификации (алгоритм обучения
- 15. Пусть имеются алгоритмы классификации
- 16. Если в постановке задачи рассматривается множество обучающих
Слайд 2План лекции
Классификация моделей, прямая и
обратная задачи, виды моделирования.
Процесс моделирования, критерий выбора.
Стандартные
Алгоритмы обучения классификации, их характеристики и способы сравнения.
Слайд 3Математическая модель
Математическая модель – математическое представление реальности, один из вариантов модели,
Замена объекта исследования его моделью
Связь с реальностью – гипотезы, идеализация, упрощение
Методы, как правило, описывают идеальный объект
Универсальные модели разного уровня адекватности
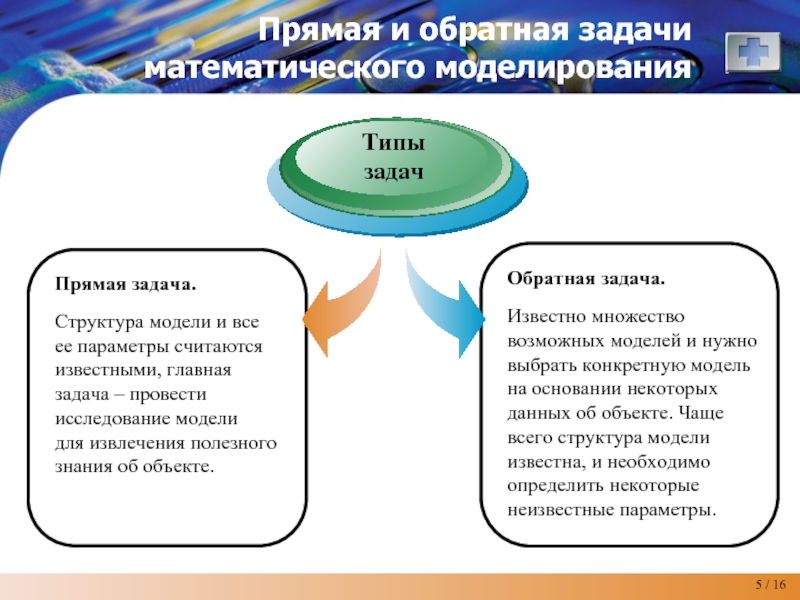
Слайд 5Прямая и обратная задачи математического моделирования
Прямая задача.
Структура модели и все
Типы
задач
Обратная задача.
Известно множество возможных моделей и нужно выбрать конкретную модель на основании некоторых данных об объекте. Чаще
всего структура модели известна, и необходимо определить некоторые неизвестные параметры.
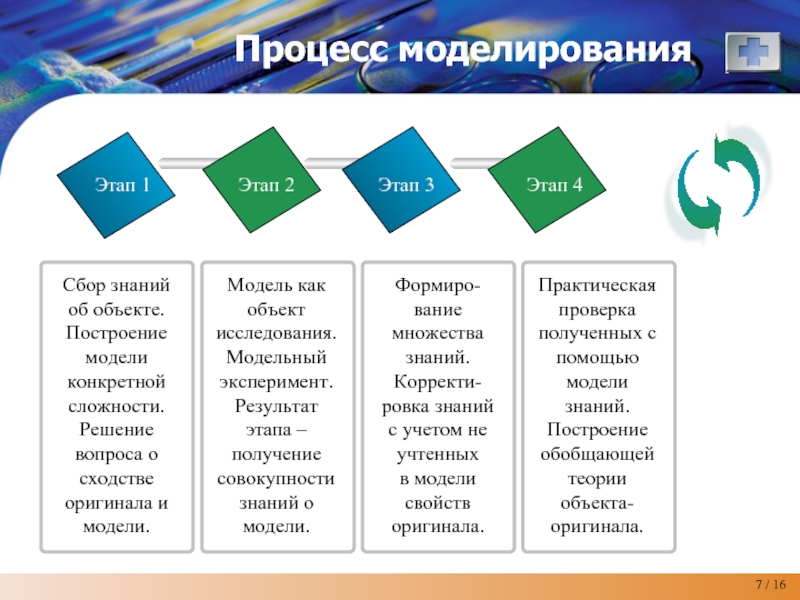
Слайд 7Процесс моделирования
Этап 1
Этап 2
Этап 3
Этап 4
Сбор знаний об объекте.
Построение модели конкретной
Решение вопроса о сходстве оригинала и модели.
Модель как объект исследования. Модельный эксперимент. Результат этапа – получение совокупности знаний о модели.
Формиро-вание множества знаний. Корректи-ровка знаний с учетом не учтенных
в модели свойств оригинала.
Практическая проверка полученных с помощью модели знаний. Построение обобщающей теории объекта-оригинала.
Слайд 8Критерии выбора моделей и
методы отбора признаков
Внешние критерии:
адекватность, непротиворечивость,
полнота, точность, универсальность
Внутренние
Отбор признаков осуществляется по принципу их значимости с точки зрения удовлетворения критериям к выбору (построению) модели. Бывают случаи, когда объекты описываются временными рядами, сигналами, изображениями, видеорядами, текстами, попарными отношениями сходства или интенсивности взаимодействия.
Слайд 9
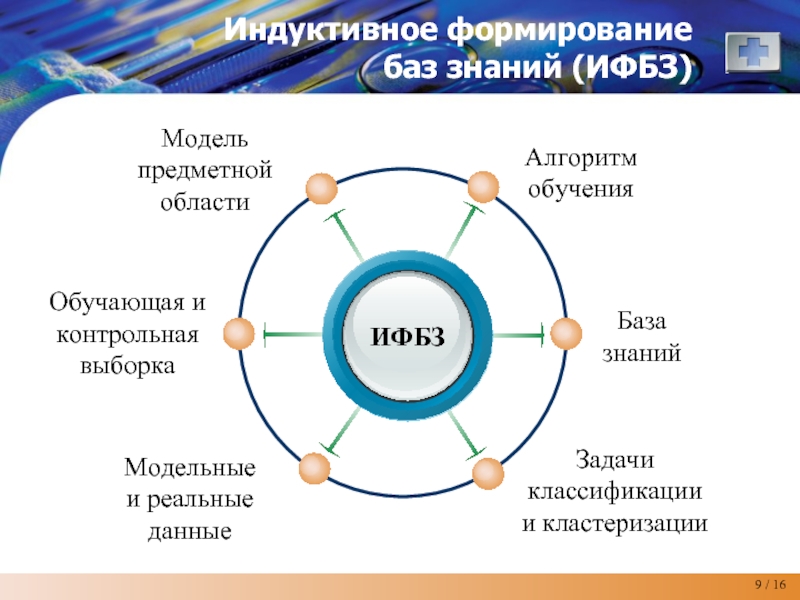
ИФБЗ
Алгоритм
обучения
Модель
предметной
области
База
знаний
Задачи
классификации
и кластеризации
Обучающая и
контрольная
выборка
Модельные
и реальные
данные
Индуктивное формирование
баз знаний (ИФБЗ)
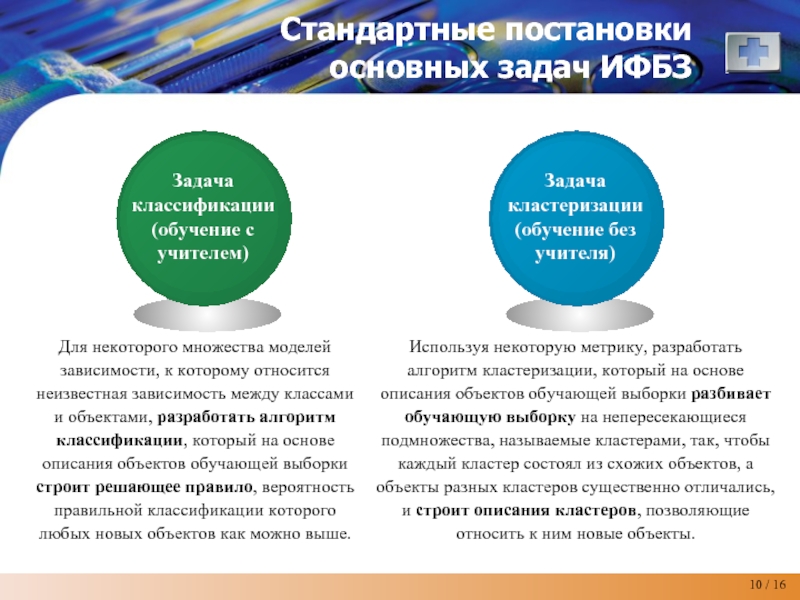
Слайд 10Стандартные постановки
основных задач ИФБЗ
Для некоторого множества моделей зависимости, к которому относится
Используя некоторую метрику, разработать алгоритм кластеризации, который на основе описания объектов обучающей выборки разбивает обучающую выборку на непересекающиеся подмножества, называемые кластерами, так, чтобы каждый кластер состоял из схожих объектов, а объекты разных кластеров существенно отличались, и строит описания кластеров, позволяющие относить к ним новые объекты.
Слайд 11Правильная и точная классификации
Правильная
классификация
– если одним из классов объекта, выдаваемых решающим
Точная
классификация
– если решающее правило выдает для объекта единственный класс.
Учитель –
либо сама обучающая выборка,
либо тот,
кто указал
на объектах обучающей выборки их правильные классы.
Слайд 12Отличия задач
классификации и кластеризации
Задача кластеризации отличается от задачи классификации тем, что
Задача кластеризации сводится к разбиению обучающей выборки на непересекающиеся подмножества, называемые кластерами, так, чтобы каждый кластер состоял из схожих объектов, а объекты разных кластеров существенно отличались, а также к построению описания кластеров, позволяющим относить к этим кластерам новые объекты.
Слайд 13Компоненты формирования
Индуктивная база знаний
формирование
Обучающая
выборка
Алгоритм
обучения
Постановка
задачи
Модель
Слайд 14Алгоритм
обучения классификации
Алгоритм классификации (алгоритм обучения классификации) – это отображение, которое по
Поскольку задача поиска наибольшего значения для всех возможных алгоритмов классификации и обучающих выборок не имеет шансов быть решенной, как правило, рассматривается более конкретная постановка задачи классификации, например, задача чемпионата мира среди алгоритмов классификации.
Слайд 15Пусть имеются алгоритмы классификации
В соответствии с этой постановкой задачи проводятся чемпионаты мира среди алгоритмов классификации ( считается победителем среди участников ).
Во многих работах предлагаемый алгоритм сравнивается таким способом с другими известными алгоритмами классификации.
Задача чемпионата мира среди алгоритмов классификации (слабая)
Слайд 16Если в постановке задачи рассматривается множество обучающих выборок
Сильная постановка задачи классификации поддерживается распределенной системой тестирования алгоритмов классификации «Полигон алгоритмов».
Задача чемпионата мира среди алгоритмов классификации (сильная)