ММ в ИР
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математические методы в инженерных расчетах презентация
Содержание
- 1. Математические методы в инженерных расчетах
- 2. Цель уметь решать сложные инженерные
- 3. Литература ВОЗНЕСЕНСКИЙ В.А., ЛЯШЕНКО Т.В., ОГАРКОВ Б.Л.
- 4. Назначение ЧМ, их сущность
- 5. Теоретическая база Математический анализ Техническая база АМ
- 6. Осуществляется замена функции дискретным набором чисел −
- 7. Такая замена «целого» «частью» − всей функции
- 8. Всегда нужно оценивать, как далеко оценка результата
- 9. Осуществляется пошаговый – итерационный процесс Особенность
- 10. Процесс последовательного пошагового приближения к
- 11. В основе использования ЧМ – Математическая
- 12. Система (Материал, борщ, конструкция, плотина, цех,
- 13. Математическая Модель – формально-знаковое описание системы,
- 14. Работать с моделями и увидеть, как ЧМ
- 15. Путь от модели к результату 0.
- 16. Группы задач и методов
- 17. Общее для всех методов Получение результата
Слайд 1Математические методы
в инженерных расчетах
Татьяна Васильевна Ляшенко
профессор, доктор технических наук
Кафедра прикладной и
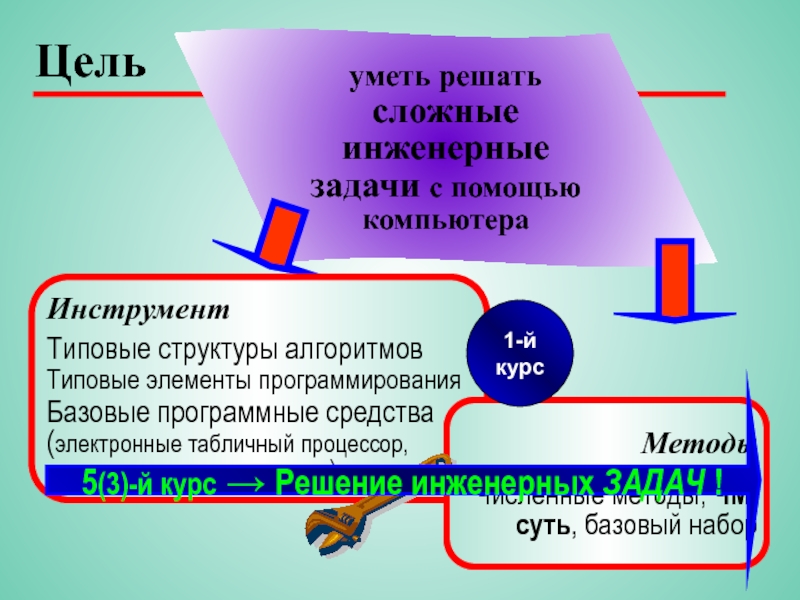
Слайд 2Цель
уметь решать
сложные инженерные задачи с помощью компьютера
Инструмент
Типовые структуры алгоритмов
Типовые элементы программирования
Базовые
(электронные табличный процессор, среда программирования, …)
Методы
Численные методы, ЧМ:
суть, базовый набор
1-й курс
5(3)-й курс → Решение инженерных ЗАДАЧ !
Слайд 3Литература
ВОЗНЕСЕНСКИЙ В.А., ЛЯШЕНКО Т.В., ОГАРКОВ Б.Л.
Численные методы решения строительно-технологических задач
2. ТУРЧАК Л.И. Основы численных методов. − М.: Наука, 1987. − 318 с.
Основная
Методическая
4.-5. … 6. Методические указания по вычислению погрешностей на персональных ЭВМ / Составитель − В.В. Никоненко. − Одесса, 1992. − 45 с.
Дополнительная 7. – 10.
3. Математичні методи розв’язання інженерних задач.
Методичні вказівки до контрольних (самостійних) завдань для студентів усіх спеціальностей / Вітюк О.Н., Денисенко В.Ю. – Одеса, 2002. – 29 с.
Слайд 4 Назначение ЧМ, их сущность
и основные понятия
Предназначены для решения сложных инженерных задач, которые нельзя решить другими методами (аналитическими, «тыка»)
ЧМ − методы, основанные
на последовательных вычислениях,
на последовательном получении и использовании чисел
В сравнении с аналитическими
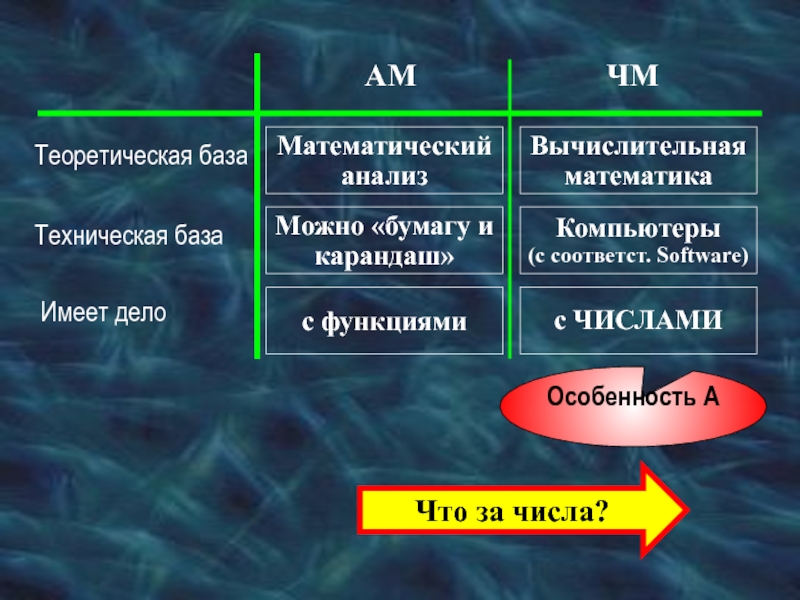
Слайд 5Теоретическая база
Математический анализ
Техническая база
АМ
ЧМ
Вычислительная математика
Можно «бумагу и карандаш»
Компьютеры
(с соответст. Software)
Имеет дело
с
с ЧИСЛАМИ
Особенность A
Что за числа?
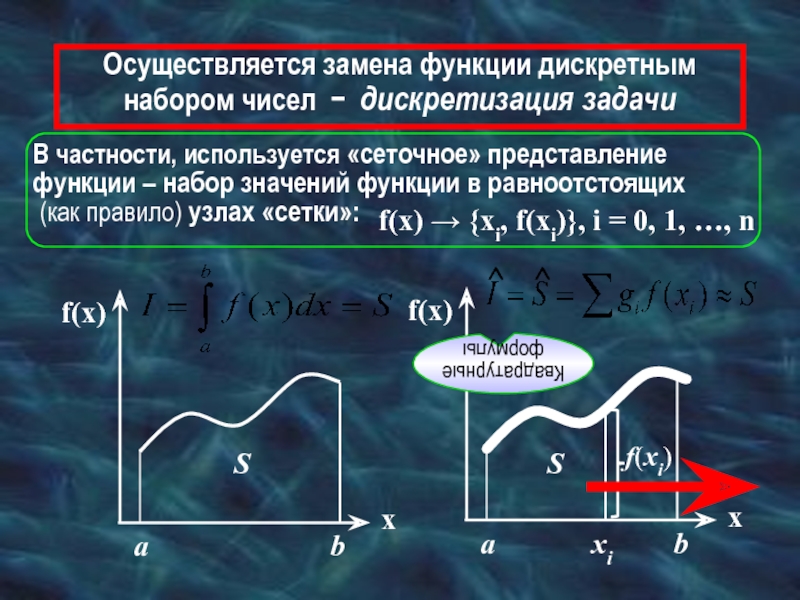
Слайд 6Осуществляется замена функции дискретным набором чисел − дискретизация задачи
a
b
В частности,
(как правило) узлах «сетки»:
f(x) → {xi, f(xi)}, i = 0, 1, …, n
S
Квадратурные формулы
Слайд 7Такая замена «целого» «частью» − всей функции отдельными значениями (а также
В результате всегда приближенное решение
B
Обозначим:
X − точное (неизвестное) решение задачи
В частности: вектор (x1, x2, … xk) – решение СЛАУ;
корень уравнения; функция – решение
дифференциального уравнения …
Слайд 8Всегда нужно оценивать, как далеко оценка результата от истины, поскольку всегда
Δ X − ошибка, погрешность приближенного решения
Она должна быть «разумной»
(строительство туалета и космического корабля)
Поэтому задается норматив точности − достаточно малое число ε
(максимальная допустимая ошибка)
– заданная точность
Δ X должна быть не больше ε, Δ X ≤ ε
Как этого добиваются?
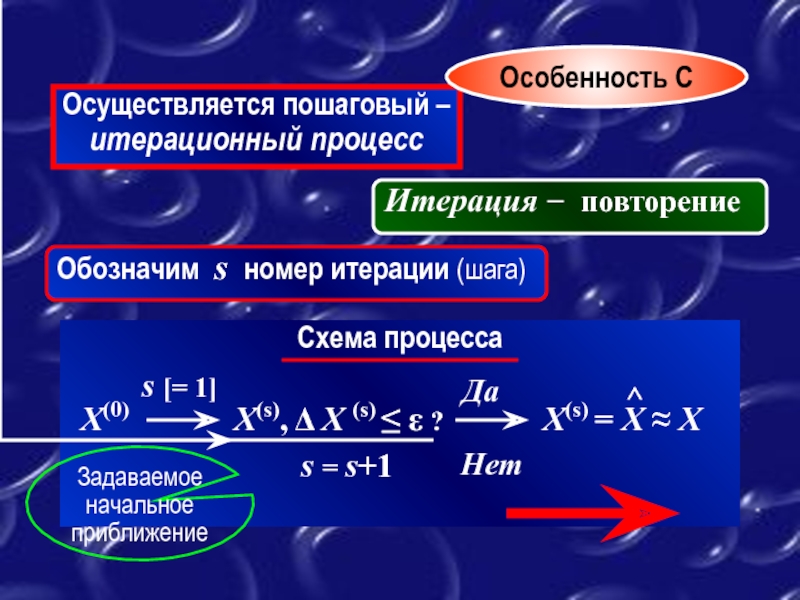
Слайд 9Осуществляется пошаговый – итерационный процесс
Особенность C
Итерация − повторение
Обозначим
Схема процесса
X(0)
s [= 1]
X(s), Δ X (s) ≤ ε ?
Задаваемое начальное приближение
Слайд 10Процесс последовательного
пошагового приближения
к решению задачи с заданной точностью
из
To be continued
Слайд 11В основе использования ЧМ – Математическая Модель (ММ)
физических, физико-химических,
конструкционных,
(систем)
для чего нужна ММ и что это?
ЧМ нужны числа. Числа можно взять из математического описания системы.
Для этого представим ее формально в виде схемы
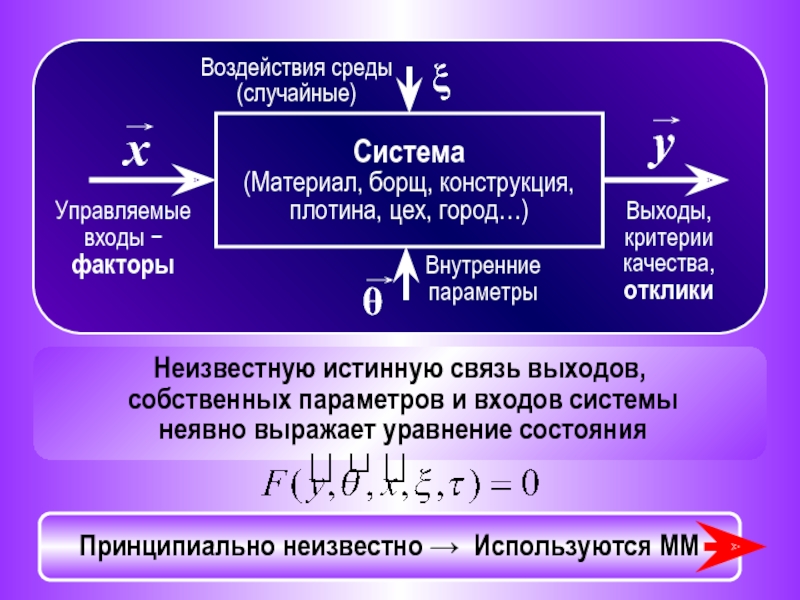
Слайд 12
Система
(Материал, борщ, конструкция, плотина, цех, город…)
Управляемые входы − факторы
Выходы, критерии качества,
Неизвестную истинную связь выходов,
собственных параметров и входов системы
неявно выражает уравнение состояния
Принципиально неизвестно → Используются ММ
Слайд 13Математическая Модель –
формально-знаковое описание системы,
которое позволяет судить
о некоторых чертах
см. про ММ Введение до середины стр. 18
ММ нужны для:
1) прогнозирования, x → y
2) проектирования, y(x) → θ
3) принятия решений, yтр → x
Пример – простейшая модель:
Rб = θ1Rц(Ц/В – θ2) (МПа)
Слайд 14Работать с моделями и увидеть, как ЧМ работают с ММ помогают
«Карты» с линиями равного уровня
(изогипсы, изобары, изотермы…)
y = f (x1, x2) = C = const →
линии равной прочности,
изолинии плотности, …
см. стр. 17, рис. В.4
NB!
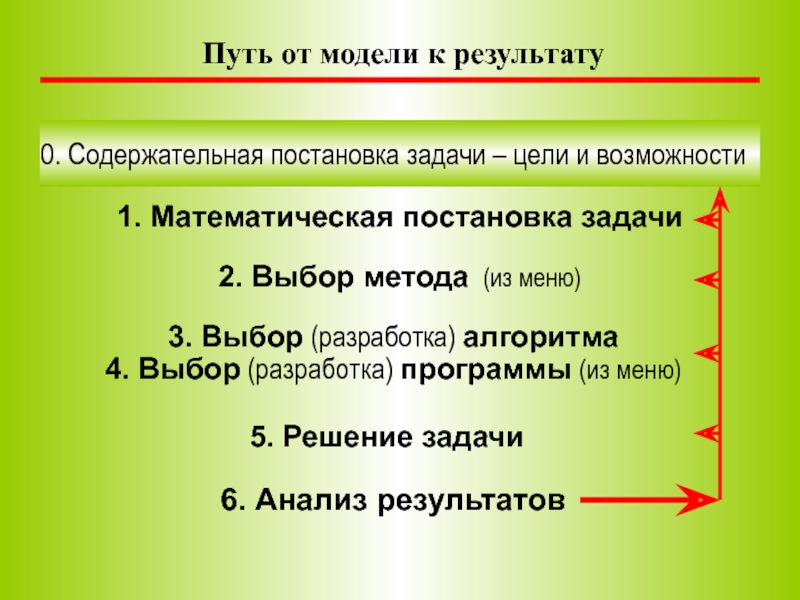
Слайд 15Путь от модели к результату
0. Содержательная постановка задачи – цели
6. Анализ результатов
1. Математическая постановка задачи
2. Выбор метода (из меню)
3. Выбор (разработка) алгоритма
4. Выбор (разработка) программы (из меню)
5. Решение задачи
Слайд 16Группы задач и методов
Методы аппроксимации
Методы решения уравнений
Методы
Численное интегрирование и дифференцирование
Решение дифференциальных уравнений
Методы оптимизации
Общее
Слайд 17
Общее для всех методов
Получение результата
в виде совокупности чисел
(или одного
с помощью конечного числа
арифметических и логических операций над числами
The End
of #1