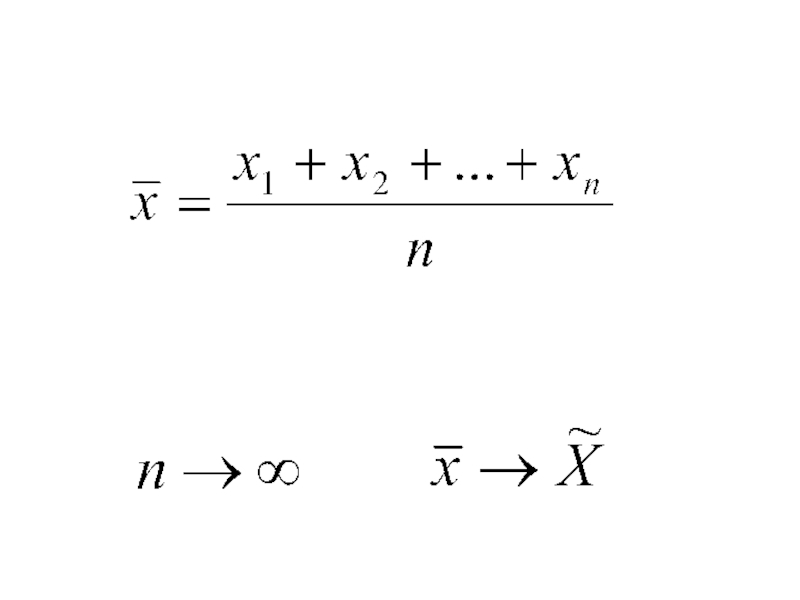- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математическая обработка результатов измерений презентация
Содержание
- 1. Математическая обработка результатов измерений
- 2. Расхождение между истинным значением определяемой величины и
- 3. 1. Виды погрешностей
- 4. 1. Систематические погрешности - это погрешности, вызванные
- 5. ПРИЧИНА постоянно действующий фактор, не изменяющийся от измерения к измерению.
- 6. УСТРАНЕНИЕ: сверка с эталонами, исправление прибора и,
- 7. 2. Промахи - это результаты, выпадающие из общего ряда измерений.
- 8. ПРИЧИНА невнимание экспериментаторов, нечеткая градуировка прибора и т. д.
- 9. УСТРАНЕНИЕ: при обработке обычно отбрасывают.
- 10. 3. Случайные погрешности - это погрешности, вызванные
- 11. ПРИЧИНЫ вызываются причинами, влияние которых изменяется от
- 12. УСТРАНЕНИЕ: с помощью математической обработки результатов измерений.
- 13. 2. Случайные погрешности измерений
- 14. Целью математической обработки результатов измерений является
- 15. Свойства случайных погрешностей – для данных
- 16. Свойства случайных погрешностей – большие по
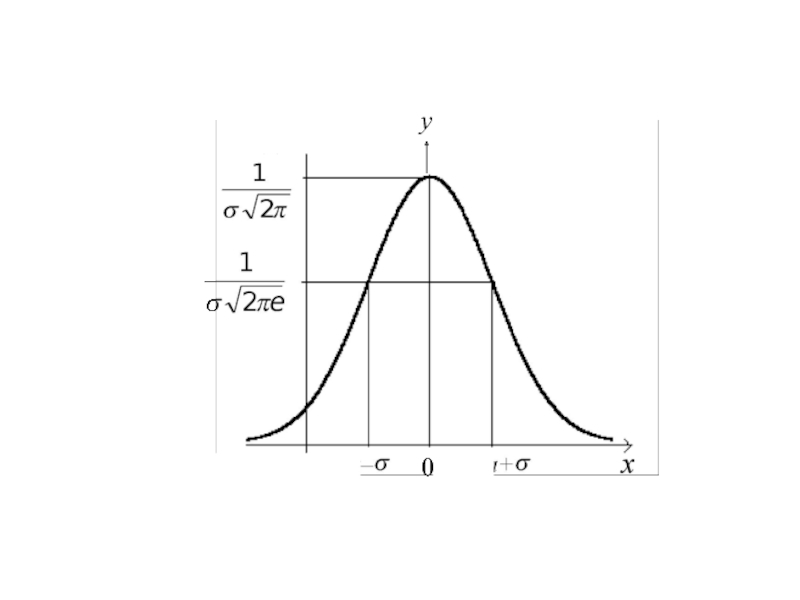
- 17. y 0
- 18. 3. Оценка истинного значения измеряемой величины
- 19. Если все измерения некоторой величины произведены с одинаковой точностью, то они называются равноточными.
- 20. истинное значение измеряемой величины х1, х2,
- 21. 3. 1 Точечная оценка
- 22. Точечной оценкой называют статистическую оценку, которая определяется одним числом
- 24. 3. 2 Интервальная оценка
- 25. Задача интервальной оценки: по данным выборки
- 26. и задана вероятность p, близкая к единице
- 28. Ширина доверительного интервала определяется по формуле:
- 29. 4. Оценка точности измерений
- 30. Точность измерения в случае точечной оценки
- 31. Точность измерения в случае точечной оценки Среднеквадратическая ошибка (стандарт):
- 33. Точность измерения в случае точечной оценки Коэффициент вариации (относительная среднеквадратическая ошибка)
- 35. Точность измерения в случае интервальной оценки Ширина доверительного интервала:
- 36. Точность измерения в случае интервальной оценки Относительная погрешность:
- 37. Проведен химический анализ чистого образца BaCl⋅2H2O на
- 38. 1. Определим среднее арифметическое ряда измерений
- 39. 2. Рассчитаем абсолютную погрешность каждого отдельного измерения:
- 40. 3. Вычислим величину исправленного среднего квадратического отклонения:
- 41. 4. Определим значение ширины доверительного интервала:
- 42. 5. Найдем относительную ошибку:
- 43. Вывод: После шести измерений установлено,
- 44. 5. Сравнительные исследования
- 45. УСЛОВИЕ 1 Сравниваемые серии измерений
- 46. Пример 1: В таблице приведены
- 47. Пример 1:
- 48. Пример 1:
- 49. Пример 1: Следовательно, сравниваемые комплексы измерений статистически устойчиво отличаются.
- 50. Пример 1: Сравниваемые серии измерений
- 51. УСЛОВИЕ 2 Сравниваемые комплексы измерений
- 52. Пример 2: Для указанных в
- 53. Пример 2: t(5; 0,95)=2,78; δ1=0,033; δ2=0,028
- 54. Диалог на экзамене. Преподаватель: - Что
Расхождение между истинным значением определяемой величины и полученным результатом измерения носит название погрешности измерения
(ошибки измерения).
Слайд 1Математическая обработка результатов измерений
1. Виды погрешностей.
2. Случайные погрешности измерений.
3. Оценка истинного значения измеряемой величины.
4. Оценка точности измерений.
5. Сравнительные исследования.
Слайд 2Расхождение между истинным значением определяемой величины и полученным результатом измерения носит
название погрешности измерения
(ошибки измерения).
Слайд 41. Систематические погрешности -
это погрешности, вызванные каким-либо постоянным воздействием, которое во
время измерения нельзя устранить.
Слайд 6УСТРАНЕНИЕ:
сверка с эталонами, исправление прибора и, в целом, устранение
известного мешающего фактора.
Главная палата
мер, весов и часов
Слайд 103. Случайные погрешности -
это погрешности, вызванные влиянием различных случайных факторов, влияние
которых и их значение во время измерения нельзя предусмотреть;
в виду этого при различных измерениях погрешности могут менять свой знак и величину, причем нельзя заранее указать ее значение.
Слайд 11ПРИЧИНЫ
вызываются причинами, влияние которых изменяется от измерения к измерению, и эти
причины не могут быть учтены.
Слайд 14Целью математической обработки результатов измерений
является оценка величины случайных погрешностей и
определение интервалов, в которых с необходимой степенью надежности находится истинное значение измеряемого признака.
Слайд 15Свойства
случайных погрешностей
– для данных условий измерений случайные ошибки не могут
превосходить по модулю известного предела;
– при достаточно большом количестве измерений случайные ошибки, одинаковые по величине, но различные по знаку, встречаются одинаково часто;
– при достаточно большом количестве измерений случайные ошибки, одинаковые по величине, но различные по знаку, встречаются одинаково часто;
Слайд 16Свойства
случайных погрешностей
– большие по абсолютной величине ошибки встречаются намного реже,
чем малые, то есть вероятность появления ошибки уменьшается с ростом величины ошибки;
– с увеличением числа измерений среднее арифметическое случайных ошибок одинаковой точности измерений одной и той же величины неограниченно стремится к нулю.
– с увеличением числа измерений среднее арифметическое случайных ошибок одинаковой точности измерений одной и той же величины неограниченно стремится к нулю.
Слайд 19Если все измерения некоторой величины произведены с одинаковой точностью, то они
называются равноточными.
Слайд 25Задача
интервальной оценки:
по данным выборки построить такой числовой интервал (доверительный), внутри
которого с заранее заданной вероятностью, близкой к единице, будет находиться оцениваемый параметр.
Слайд 26и задана вероятность p, близкая к единице (доверительная вероятность).
Требуется найти такое
значение δ, чтобы интервал
Слайд 28Ширина доверительного интервала определяется по формуле:
где, число t(n,p) определяется по
специальным таблицам критических точек распределения Стьюдента;
σ* – исправленное среднее квадратическое отклонение.
σ* – исправленное среднее квадратическое отклонение.
Слайд 30Точность измерения в случае точечной оценки
Средней абсолютной ошибкой называется среднее
арифметическое модулей всех ошибок:
Слайд 33Точность измерения в случае точечной оценки
Коэффициент вариации (относительная среднеквадратическая ошибка)
Слайд 37Проведен химический анализ чистого образца BaCl⋅2H2O на процентное содержание Ba. Получены
следующие результаты:
56,10%, 56,05%, 56,00%,
55,95%, 56,30%, 55,83%.
Провести обработку результатов измерений при надежности α = 95%.
Слайд 392. Рассчитаем абсолютную погрешность каждого отдельного измерения:
= 56,10 – 56,04
= 0,06 %;
= 56,05 – 56,04 = 0,01 %;
= 56,00 – 56,04 = – 0,04 %;
= 55,95 – 56,04 = – 0,09 %;
= 56,30 – 56,04 = 0,26 %;
= 55,83 – 56,04 = – 0,21.
= 56,05 – 56,04 = 0,01 %;
= 56,00 – 56,04 = – 0,04 %;
= 55,95 – 56,04 = – 0,09 %;
= 56,30 – 56,04 = 0,26 %;
= 55,83 – 56,04 = – 0,21.
Слайд 43Вывод:
После шести измерений установлено, что с надежностью 95% содержание Ba
находится в интервале (55,87%; 56,21%).
Относительная ошибка измерений 0,3 %
Относительная ошибка измерений 0,3 %
Слайд 45УСЛОВИЕ 1
Сравниваемые серии измерений различаются в том случае, если выполняется неравенство:
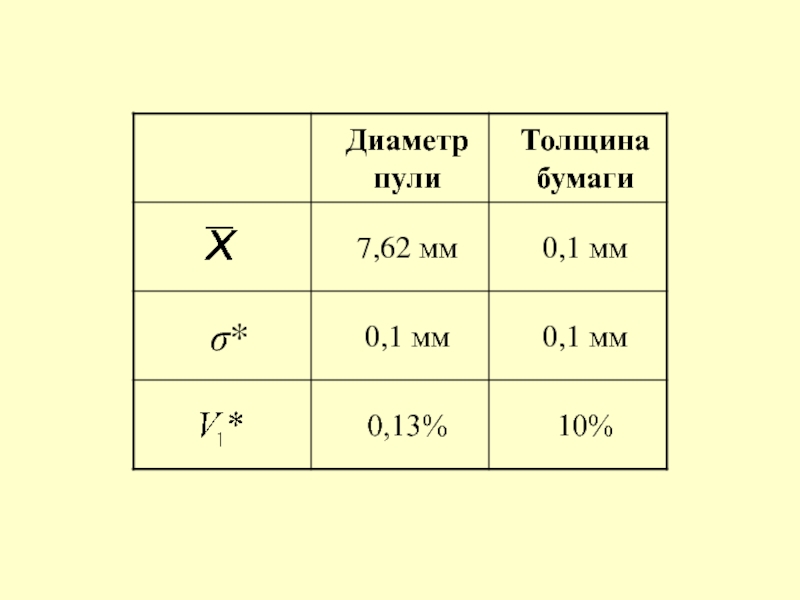
Слайд 46Пример 1:
В таблице приведены результаты определения толщины двух кусков проволоки.
Различаются
ли статистически устойчиво оценки результатов?
Слайд 49Пример 1:
Следовательно, сравниваемые комплексы измерений статистически устойчиво отличаются.
Слайд 50Пример 1:
Сравниваемые серии измерений различаются в том случае, если выполняется неравенство:
Слайд 51УСЛОВИЕ 2
Сравниваемые комплексы измерений статистически устойчиво различаются с данной степенью вероятности
р2, если доверительные интервалы, определенные для каждой серии с доверительной вероятностью р не перекрываются.
Слайд 52Пример 2:
Для указанных в примере 1 данных установить различаются ли они
статистически устойчиво.
Слайд 53Пример 2:
t(5; 0,95)=2,78; δ1=0,033; δ2=0,028
(1,417;1,483)
(1,512;1,568)
Поскольку доверительные интервалы не пересекаются,
то с вероятностью р=0,952=0,9025 можно утверждать, что эти комплексы измерений устойчиво отличаются
Слайд 54Диалог на экзамене.
Преподаватель: - Что такое лошадиная сила?
Студент: -
Это сила, какую развивает лошадь ростом в один метр и весом в один килограмм.
Преподаватель: - Где же вы такую лошадь видели?!
Студент: - А ее просто так не увидишь. Она хранится в Париже, в Палате мер и весов.
Преподаватель: - Где же вы такую лошадь видели?!
Студент: - А ее просто так не увидишь. Она хранится в Париже, в Палате мер и весов.
