- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математическая логика презентация
Содержание
- 1. Математическая логика
- 2. Контрольные вопросы по теме: Логика (определение). Логическое
- 3. Логика — это наука, изучающая
- 4. Логическое высказывание - это повествовательное предложение, о
- 5. Типы высказываний: Простое – никакая его
- 6. Составляющие логического высказывания: Субъект (S) Предикат (Р) Связка Квантор
- 7. Составляющие логического высказывания Субъект, S -
- 8. «Все компьютеры состоят из процессора, памяти и
- 9. Логические операции: Отрицание (инверсия) Конъюнкция Дизъюнкция Строгая дизъюнкция Импликация Эквиваленция
- 10. Отрицание (NOT, не, не верно, что)
- 11. Обозначения: А·В; АΛВ; А&В Конъюнкция двух высказываний
- 12. Дизъюнкция (OR, или, либо) Обозначение: А
- 13. Строгая дизъюнкция (XOR, или…или, либо…либо) Обозначение:
- 14. Импликация (если-то, следует) Обозначения: А→В, А=>В. Импликация
- 15. Эквиваленция (тождественно, равносильно) Обозначение: А=В; АВ; А~В
- 16. Основные логические союзы (связки), с помощью которых в естественном языке строятся сложные высказывания.
- 17. Неверно, что в зале №1 идет лекция
- 18. Приоритет логических операций: операции в скобках; отрицание;
- 19. Алгоритм построения таблиц истинности: Определить количество переменных.
- 20. Спасибо за внимание!
Слайд 2Контрольные вопросы по теме:
Логика (определение).
Логическое высказывание.
Типы высказываний.
Составляющие логического высказывания.
Отрицание, таблица
истинности отрицания.
Конъюнкция, таблица истинности.
Дизъюнкция, таблица истинности.
Строгая дизъюнкция, таблица истинности.
Импликация, таблица истинности.
Эквиваленция, таблица истинности.
Приоритет логических операций.
Алгоритм построения таблиц истинности.
Конъюнкция, таблица истинности.
Дизъюнкция, таблица истинности.
Строгая дизъюнкция, таблица истинности.
Импликация, таблица истинности.
Эквиваленция, таблица истинности.
Приоритет логических операций.
Алгоритм построения таблиц истинности.
Слайд 3 Логика — это наука, изучающая методы установления истинности или
ложности одних высказываний на основе истинности или ложности других высказываний.
Слайд 4Логическое высказывание - это повествовательное предложение, о котором можно сказать, истинно
оно или ложно.
Истина=1
Ложь=0
А: «дважды два равно четырем» истинно А=1,
В: «три больше пяти» всегда есть ЛОЖЬ В=0.
Слайд 5Типы высказываний:
Простое –
никакая его часть сама не является высказыванием.
Составное (сложное)
–
состоит из простых высказываний, связанных между собой логическими операциями.
Слайд 7Составляющие логического высказывания
Субъект, S -
понятие о предмете мысли
Предикат, P
-
понятие о свойствах и отношениях предмета мысли.
Субъект и предикат - термины суждения.
Связка -
отношения между субъектом и предикатом (выражается «есть», «не есть», «является», «состоит» и т.д.)
Квантор -
указывает, относится ли суждение ко всему или к части объема понятия, выражающего субъект («все», «некоторые», «многие», «ни один», и т.п.).
понятие о свойствах и отношениях предмета мысли.
Субъект и предикат - термины суждения.
Связка -
отношения между субъектом и предикатом (выражается «есть», «не есть», «является», «состоит» и т.д.)
Квантор -
указывает, относится ли суждение ко всему или к части объема понятия, выражающего субъект («все», «некоторые», «многие», «ни один», и т.п.).
Слайд 8«Все компьютеры состоят из процессора, памяти и внешних устройств»
«компьютеры» - субъект,
«процессора, памяти и внешних устройств» - предикат,
«состоят» - связка,
«все» - квантор.
«состоят» - связка,
«все» - квантор.
Слайд 9Логические операции:
Отрицание (инверсия)
Конъюнкция
Дизъюнкция
Строгая дизъюнкция
Импликация
Эквиваленция
Слайд 10Отрицание
(NOT, не, не верно, что)
Обозначения: ¬А; Ā
Инверсия высказывания истинна, когда
высказывание ложно, и ложна, когда высказывание истинно.
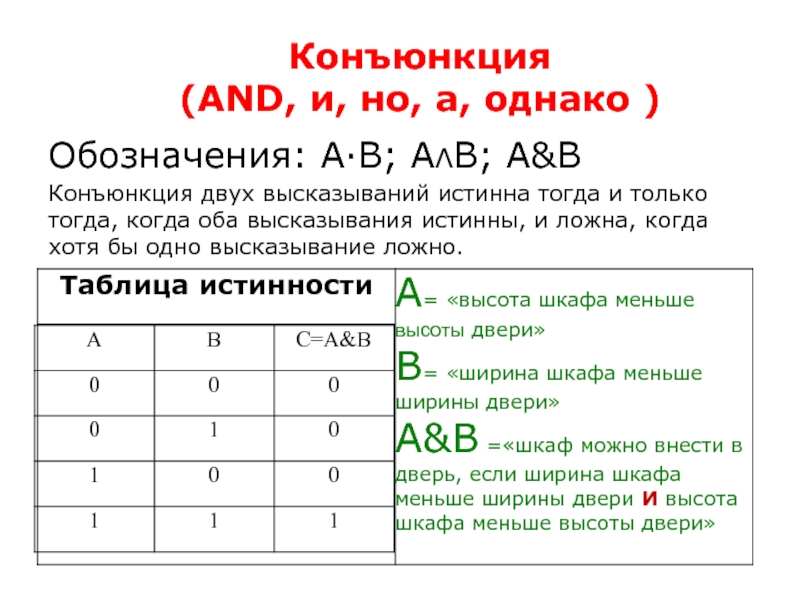
Слайд 11Обозначения: А·В; АΛВ; А&В
Конъюнкция двух высказываний истинна тогда и только тогда,
когда оба высказывания истинны, и ложна, когда хотя бы одно высказывание ложно.
Конъюнкция
(AND, и, но, а, однако )
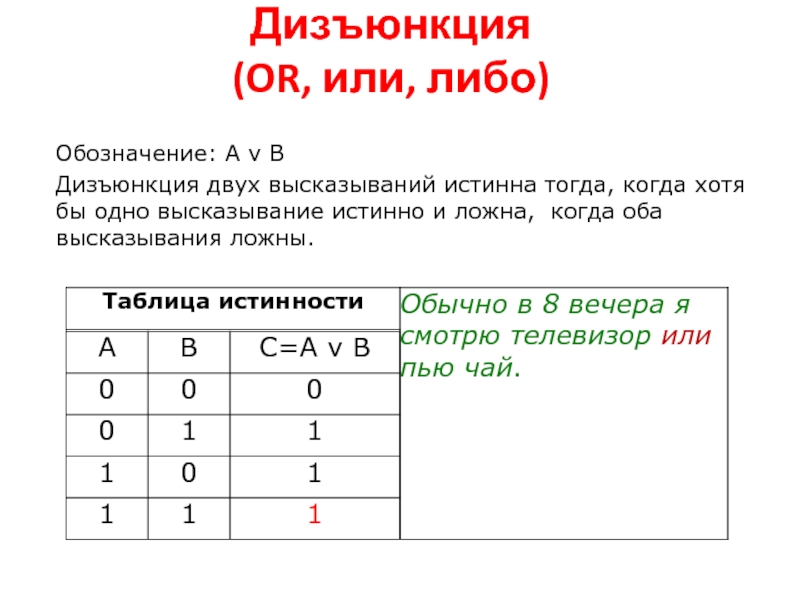
Слайд 12Дизъюнкция
(OR, или, либо)
Обозначение: А v В
Дизъюнкция двух высказываний истинна тогда,
когда хотя бы одно высказывание истинно и ложна, когда оба высказывания ложны.
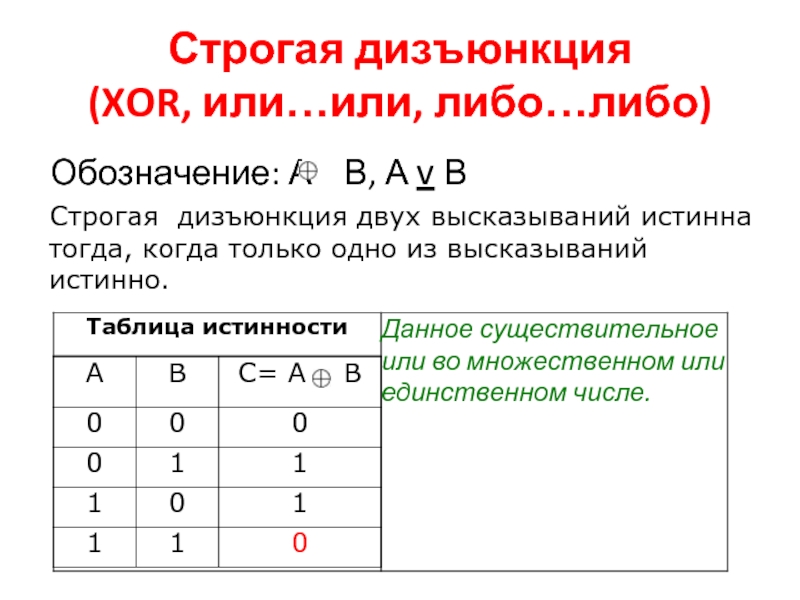
Слайд 13Строгая дизъюнкция
(XOR, или…или, либо…либо)
Обозначение: А В, А v В
Строгая
дизъюнкция двух высказываний истинна тогда, когда только одно из высказываний истинно.
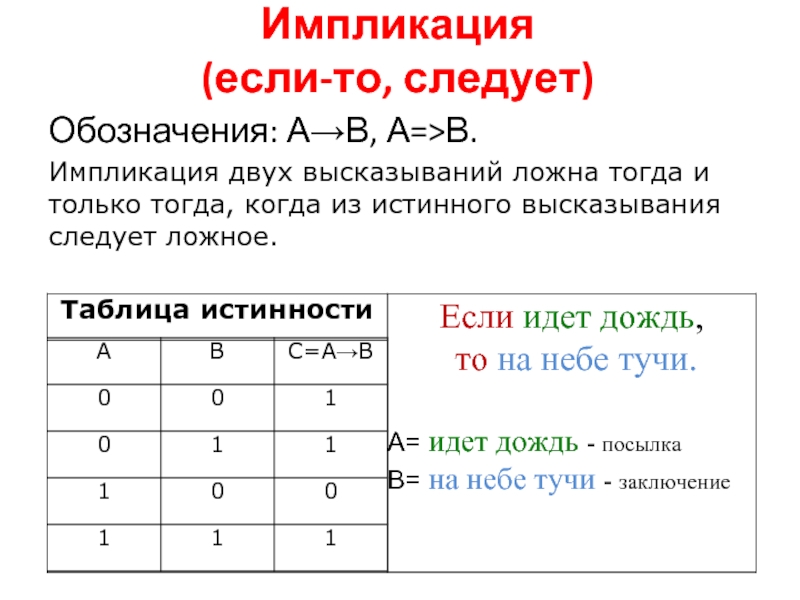
Слайд 14Импликация
(если-то, следует)
Обозначения: А→В, А=>В.
Импликация двух высказываний ложна тогда и только тогда,
когда из истинного высказывания следует ложное.
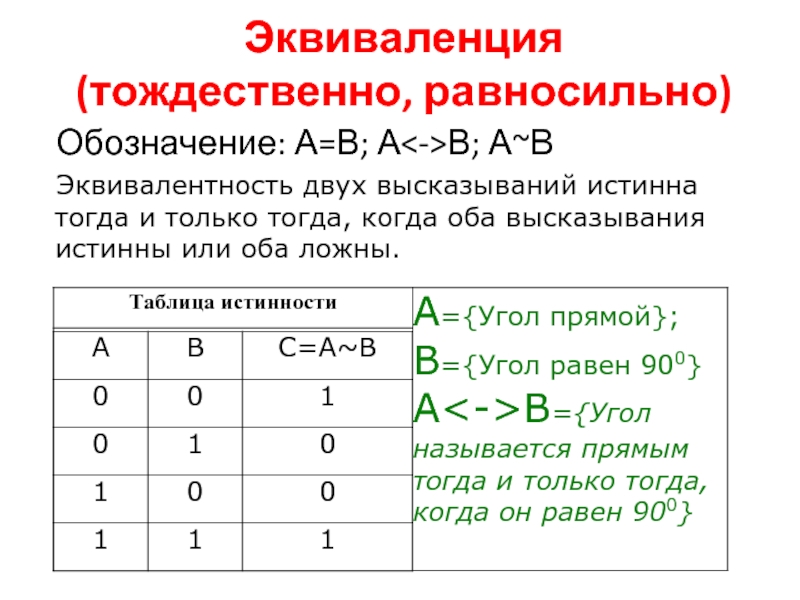
Слайд 15Эквиваленция
(тождественно, равносильно)
Обозначение: А=В; АВ; А~В
Эквивалентность двух высказываний истинна тогда и только
тогда, когда оба высказывания истинны или оба ложны.
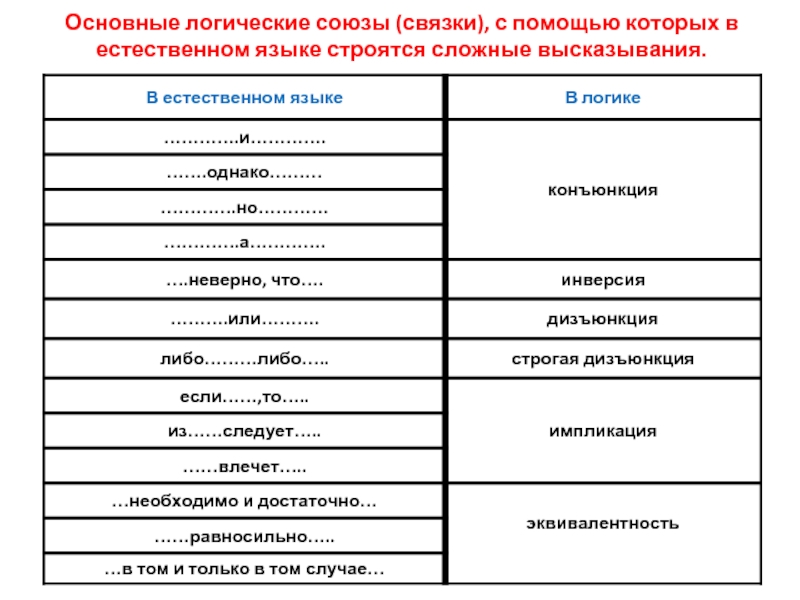
Слайд 16Основные логические союзы (связки), с помощью которых в естественном языке строятся
сложные высказывания.
Слайд 17Неверно, что в зале №1 идет лекция по психологии. Число 123 либо
четное, либо нечетное, третьего не дано.
Аня отличница, но плохая спортсменка.
Если пожелтели листья, то пришла осень.
Чтобы перейти на следующий курс достаточно сдать сессию на тройки.
Слайд 18Приоритет
логических операций:
операции в скобках;
отрицание;
конъюнкция и дизъюнкция (слева направо);
импликация;
эквиваленция.
С = (¬( A
v В) → В) ^ А
Слайд 19Алгоритм построения таблиц истинности:
Определить количество переменных.
Определить количество логических операций и последовательность
их выполнения.
Заполнить столбцы результатами выполнения логических операций в обозначенной последовательности.
Определить количество строк (К) таблицы по формуле к=2n , где n - количество переменных.
Заполнить столбцы результатами выполнения логических операций в обозначенной последовательности.
Определить количество строк (К) таблицы по формуле к=2n , где n - количество переменных.