нижний. Двигаться он может либо на клетку вправо, либо на клетку вниз. Попадая в каждую ячейку, Марио зарабатывает столько монет, сколько указано в ячейке. Какое максимальное количество монет может заработать Марио? Первая и последняя клетки считаются.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математическая игра презентация
Содержание
- 2. Мистер Марио хочет попасть из верхнего
- 3. 1. Какой длины может быть путь Марио?
- 4. 1. Какой длины может быть путь Марио?
- 5. 1. Какой длины может быть путь Марио?
- 6. 1. Какой длины может быть путь Марио?
- 7. 1. Какой длины может быть путь Марио?
- 8. 1. Какой длины может быть путь Марио?
- 9. 1. Какой длины может быть путь Марио?
- 10. 1. Какой длины может быть путь Марио?
- 11. 1. Какой длины может быть путь Марио?
- 12. 1. Какой длины может быть путь Марио?
- 13. 1. Какой длины может быть путь Марио?
- 14. 1. Какой длины может быть путь Марио?
- 15. 1. Какой длины может быть путь Марио?
- 16. 1. Какой длины может быть путь Марио?
- 17. 1. Какой длины может быть путь Марио?
- 18. 1) Посчитать длину пути 2) Посчитать количество
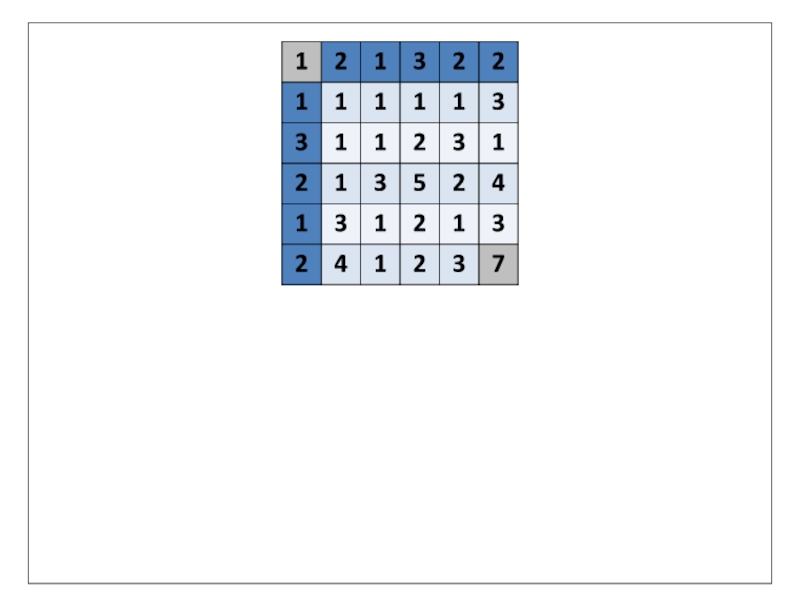
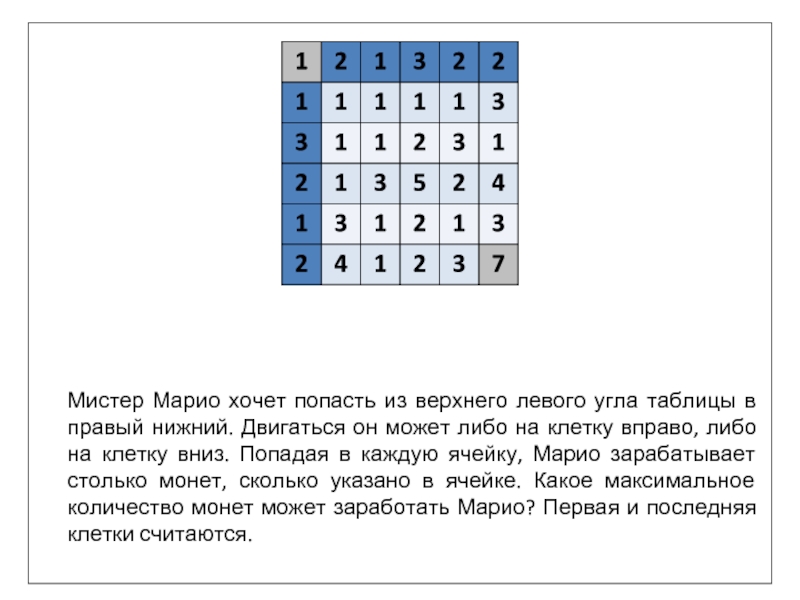
Мистер Марио хочет попасть из верхнего левого угла таблицы в правый нижний. Двигаться он может либо на клетку вправо, либо на клетку вниз. Попадая в каждую ячейку, Марио зарабатывает столько
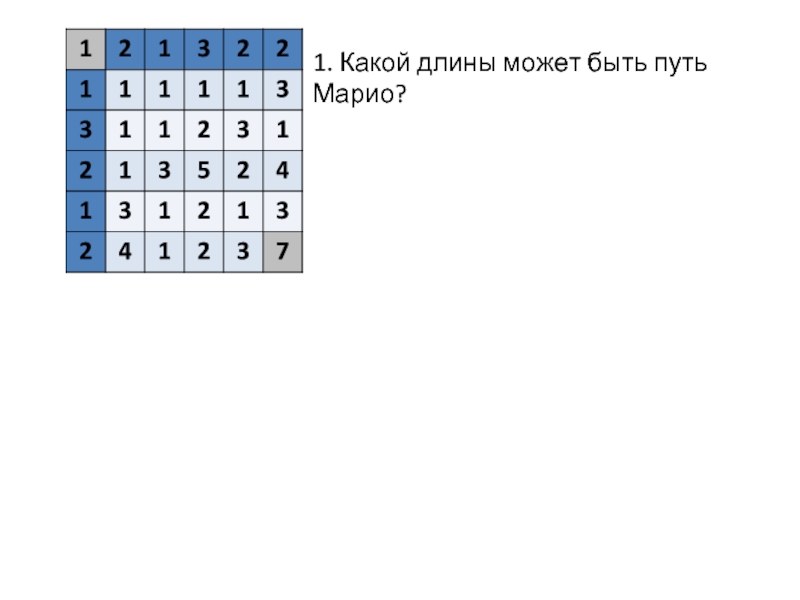
Слайд 41. Какой длины может быть путь Марио?
Оказывается длина пути не зависит
от пути и всегда равна 5+5=10
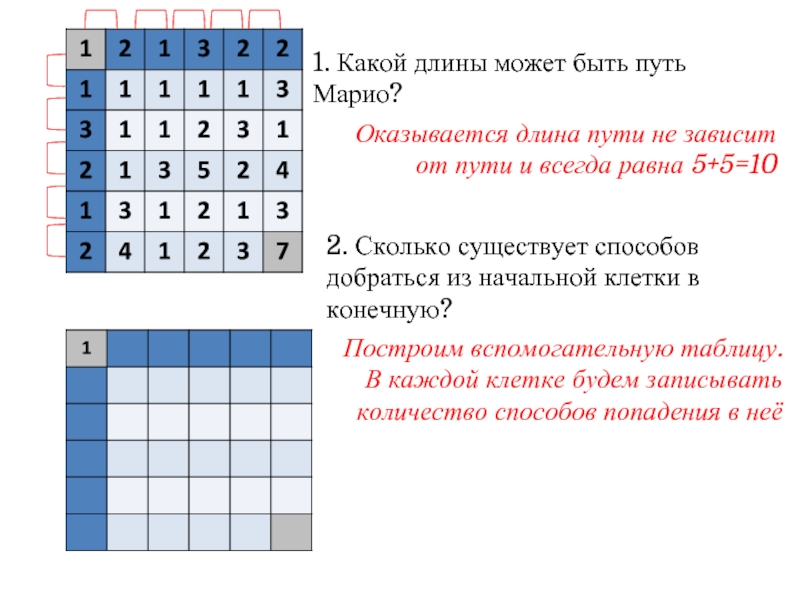
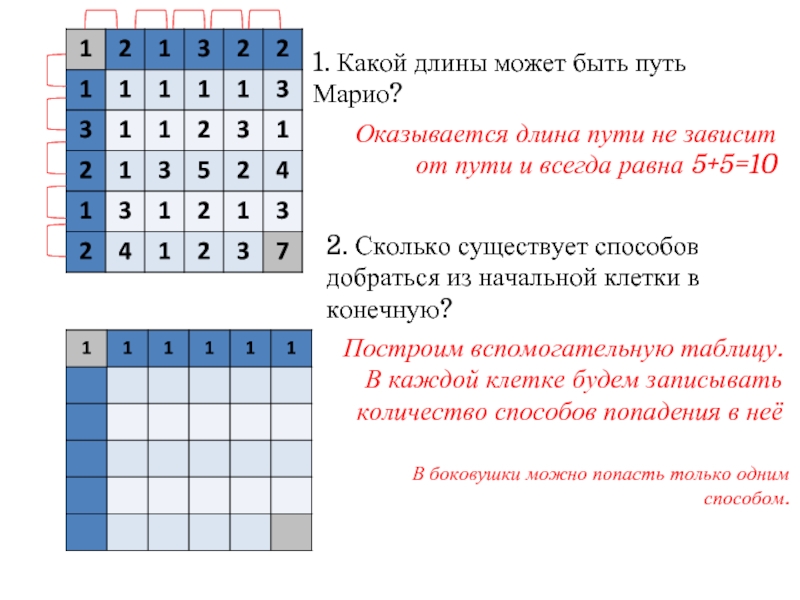
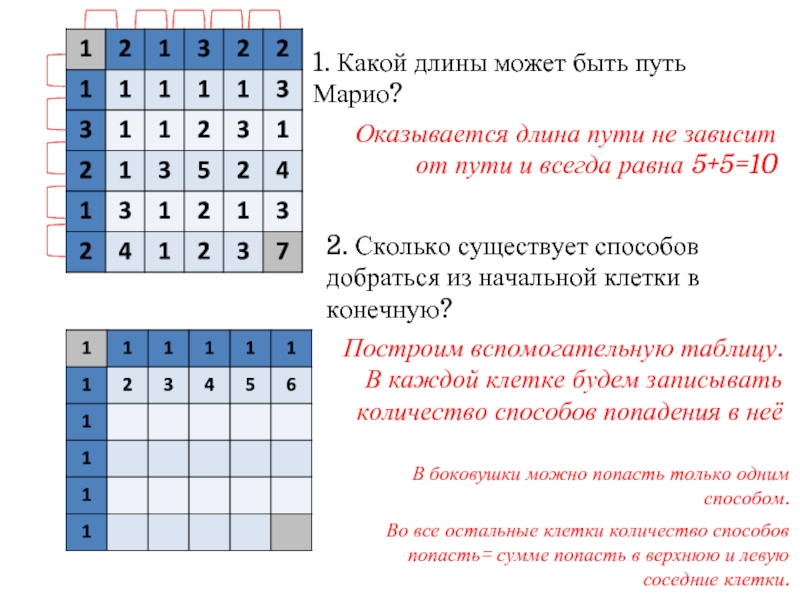
Слайд 51. Какой длины может быть путь Марио?
Оказывается длина пути не зависит
от пути и всегда равна 5+5=10
2. Сколько существует способов добраться из начальной клетки в конечную?
Ваши ставки?
Слайд 61. Какой длины может быть путь Марио?
Оказывается длина пути не зависит
от пути и всегда равна 5+5=10
2. Сколько существует способов добраться из начальной клетки в конечную?
Построим вспомогательную таблицу. В каждой клетке будем записывать количество способов попадения в неё
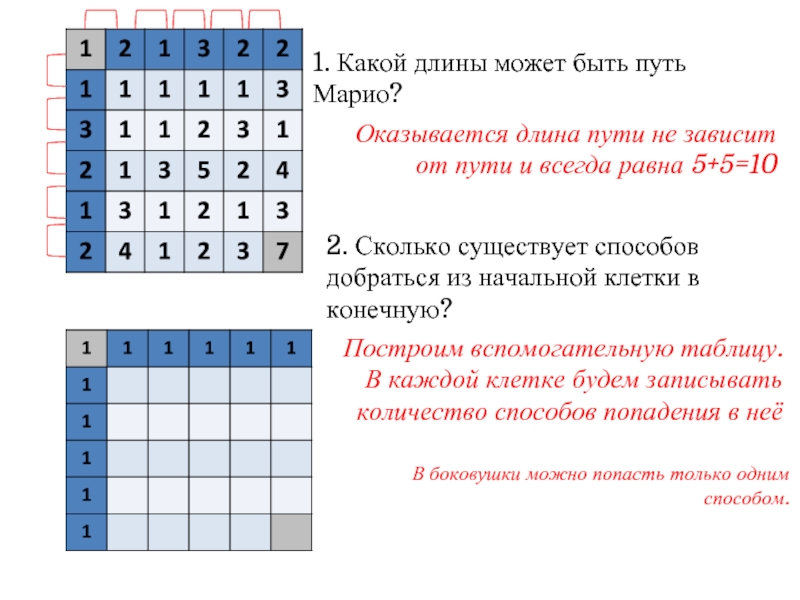
Слайд 71. Какой длины может быть путь Марио?
Оказывается длина пути не зависит
от пути и всегда равна 5+5=10
2. Сколько существует способов добраться из начальной клетки в конечную?
Построим вспомогательную таблицу. В каждой клетке будем записывать количество способов попадения в неё
В боковушки можно попасть только одним способом.
Слайд 81. Какой длины может быть путь Марио?
Оказывается длина пути не зависит
от пути и всегда равна 5+5=10
2. Сколько существует способов добраться из начальной клетки в конечную?
Построим вспомогательную таблицу. В каждой клетке будем записывать количество способов попадения в неё
В боковушки можно попасть только одним способом.
Слайд 91. Какой длины может быть путь Марио?
Оказывается длина пути не зависит
от пути и всегда равна 5+5=10
2. Сколько существует способов добраться из начальной клетки в конечную?
Построим вспомогательную таблицу. В каждой клетке будем записывать количество способов попадения в неё
В боковушки можно попасть только одним способом.
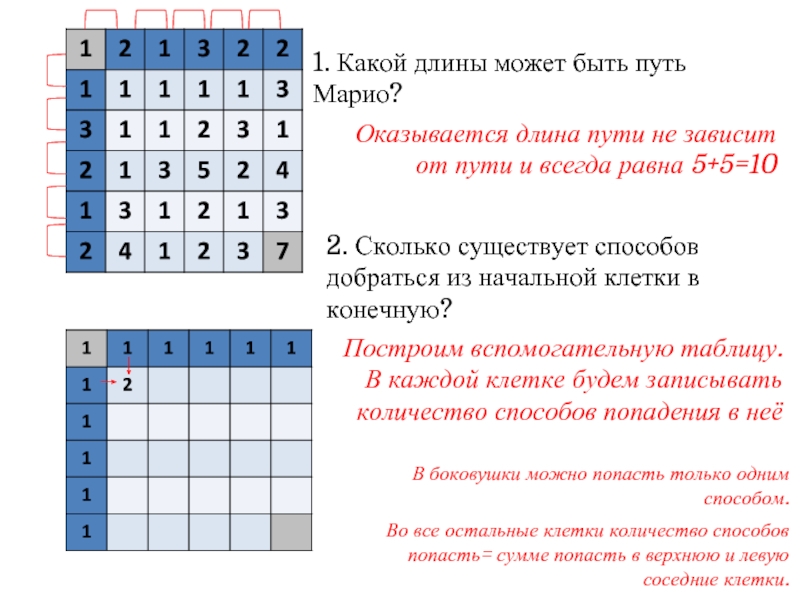
Слайд 101. Какой длины может быть путь Марио?
Оказывается длина пути не зависит
от пути и всегда равна 5+5=10
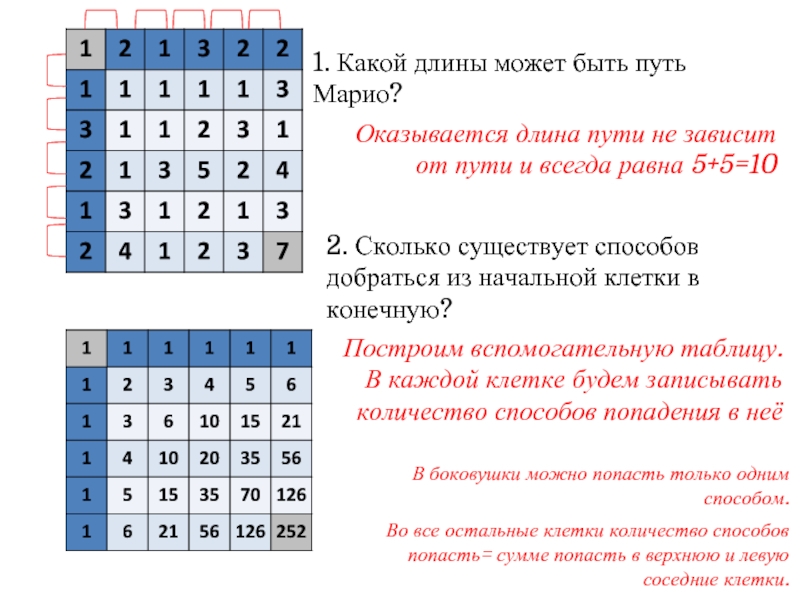
2. Сколько существует способов добраться из начальной клетки в конечную?
Построим вспомогательную таблицу. В каждой клетке будем записывать количество способов попадения в неё
В боковушки можно попасть только одним способом.
Во все остальные клетки количество способов попасть= сумме попасть в верхнюю и левую соседние клетки.
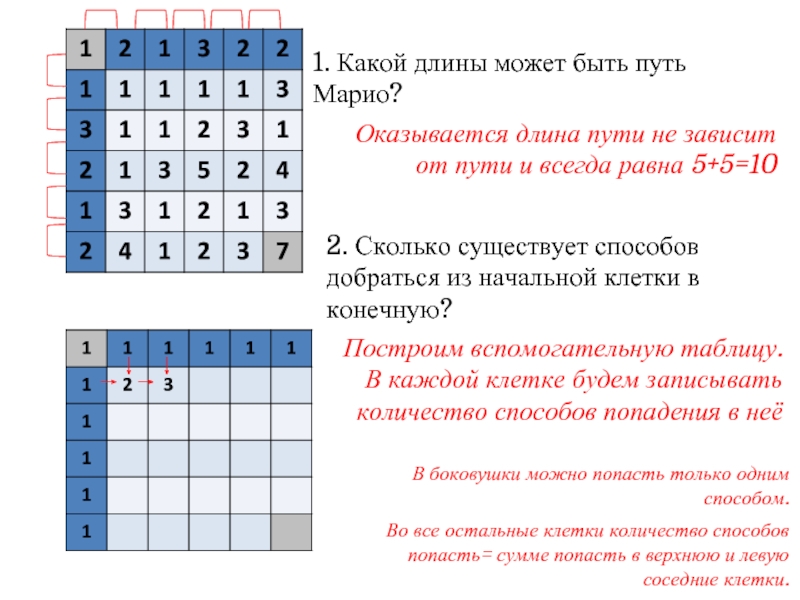
Слайд 111. Какой длины может быть путь Марио?
Оказывается длина пути не зависит
от пути и всегда равна 5+5=10
2. Сколько существует способов добраться из начальной клетки в конечную?
Построим вспомогательную таблицу. В каждой клетке будем записывать количество способов попадения в неё
В боковушки можно попасть только одним способом.
Во все остальные клетки количество способов попасть= сумме попасть в верхнюю и левую соседние клетки.
Слайд 121. Какой длины может быть путь Марио?
Оказывается длина пути не зависит
от пути и всегда равна 5+5=10
2. Сколько существует способов добраться из начальной клетки в конечную?
Построим вспомогательную таблицу. В каждой клетке будем записывать количество способов попадения в неё
В боковушки можно попасть только одним способом.
Во все остальные клетки количество способов попасть= сумме попасть в верхнюю и левую соседние клетки.
Слайд 131. Какой длины может быть путь Марио?
Оказывается длина пути не зависит
от пути и всегда равна 5+5=10
2. Сколько существует способов добраться из начальной клетки в конечную?
Построим вспомогательную таблицу. В каждой клетке будем записывать количество способов попадения в неё
В боковушки можно попасть только одним способом.
Во все остальные клетки количество способов попасть= сумме попасть в верхнюю и левую соседние клетки.
Слайд 141. Какой длины может быть путь Марио?
2. Сколько существует способов добраться
из начальной клетки в конечную?
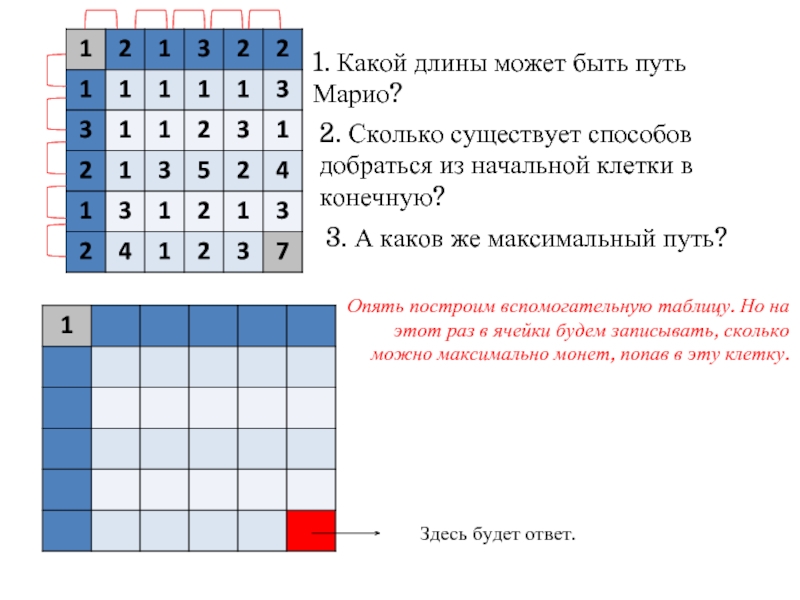
3. А каков же максимальный путь?
Опять построим вспомогательную таблицу. Но на этот раз в ячейки будем записывать, сколько можно максимально монет, попав в эту клетку.
Здесь будет ответ.
Слайд 151. Какой длины может быть путь Марио?
2. Сколько существует способов добраться
из начальной клетки в конечную?
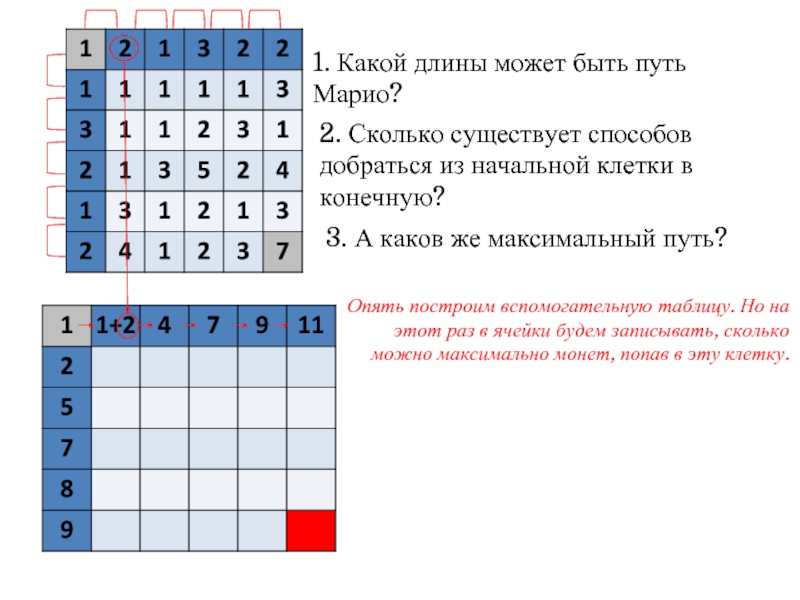
3. А каков же максимальный путь?
Опять построим вспомогательную таблицу. Но на этот раз в ячейки будем записывать, сколько можно максимально монет, попав в эту клетку.
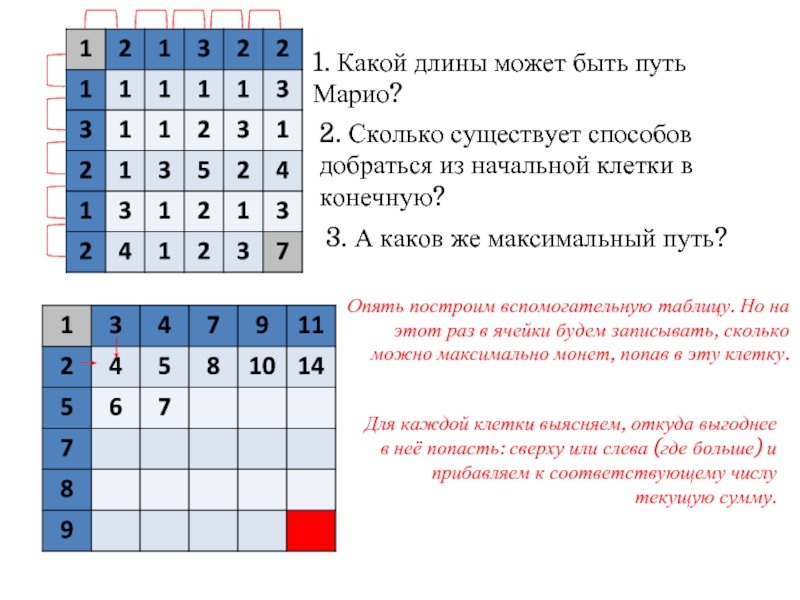
Слайд 161. Какой длины может быть путь Марио?
2. Сколько существует способов добраться
из начальной клетки в конечную?
3. А каков же максимальный путь?
Опять построим вспомогательную таблицу. Но на этот раз в ячейки будем записывать, сколько можно максимально монет, попав в эту клетку.
Для каждой клетки выясняем, откуда выгоднее в неё попасть: сверху или слева (где больше) и прибавляем к соответствующему числу текущую сумму.
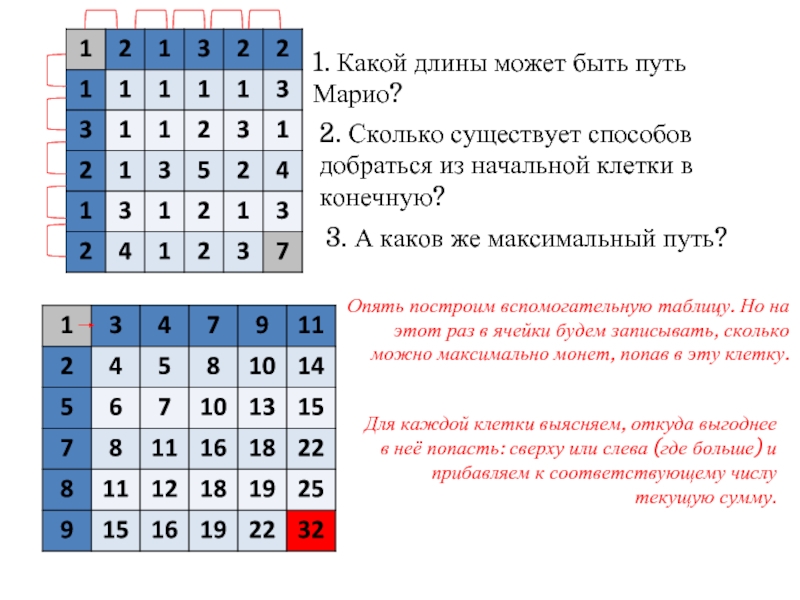
Слайд 171. Какой длины может быть путь Марио?
2. Сколько существует способов добраться
из начальной клетки в конечную?
3. А каков же максимальный путь?
Опять построим вспомогательную таблицу. Но на этот раз в ячейки будем записывать, сколько можно максимально монет, попав в эту клетку.
Для каждой клетки выясняем, откуда выгоднее в неё попасть: сверху или слева (где больше) и прибавляем к соответствующему числу текущую сумму.
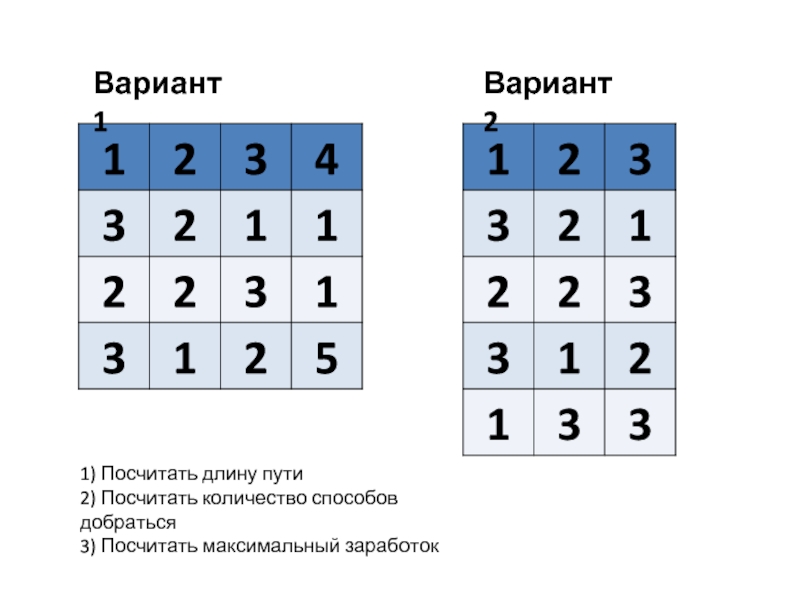
Слайд 181) Посчитать длину пути
2) Посчитать количество способов добраться
3) Посчитать максимальный заработок
Вариант
1
Вариант 2
