- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математическая экономика. Общее равновесие. (Тема 5) презентация
Содержание
- 1. Математическая экономика. Общее равновесие. (Тема 5)
- 2. 5.1. ВИДЫ И ОБЪЕКТЫ РАВНОВЕСНЫХ МОДЕЛЕЙ Математическая экономика. Лектор - Гераськин М.И., д.э.н., профессор
- 3. Равновесные модели подразделяются на модели: - частичного,
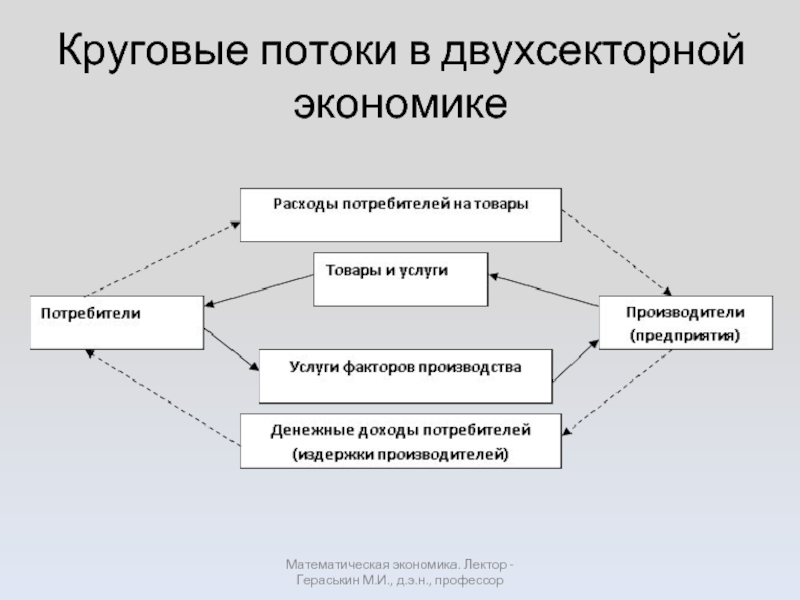
- 4. Круговые потоки в двухсекторной экономике Математическая экономика. Лектор - Гераськин М.И., д.э.н., профессор
- 5. 5.2. ПРОСТОЙ ОБМЕН В ДВУХСУБЪЕКТНОЙ ДВУХПРОДУКТОВОЙ ЭКОНОМИКЕ
- 6. Экономика состоит из двух субъектов, А и
- 7. Кривая предложения ОСA товара Y из его
- 8. Экономически кривая предложения из запаса показывает количество
- 9. Получим выражение кривой предложения из запаса, учитывая,
- 10. Выразив соотношение цен товаров из (5.3),
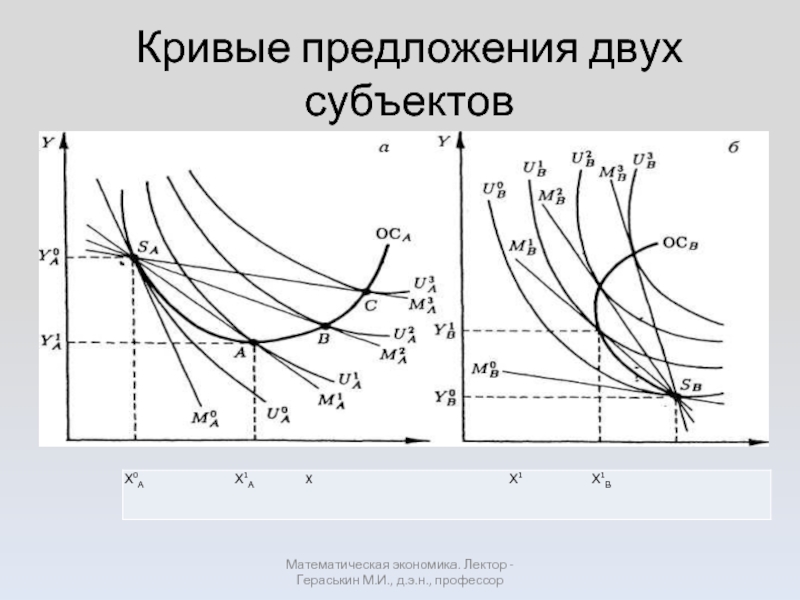
- 11. Кривые предложения двух субъектов Математическая экономика. Лектор - Гераськин М.И., д.э.н., профессор
- 12. Пример вывода выражения кривой предложения Математическая
- 13. Это уравнение определяет гиперболу, вертикальная асимптота (нуль
- 14. При этом предполагается, что
- 15. 5.3. АНАЛИЗ ОБМЕНА В ДВУХСУБЪЕКТНОЙ ДВУХПРОДУКТОВОЙ ЭКОНОМИКЕ.
- 16. Коробка Эджуорта представляет совмещенные карты безразличия двух
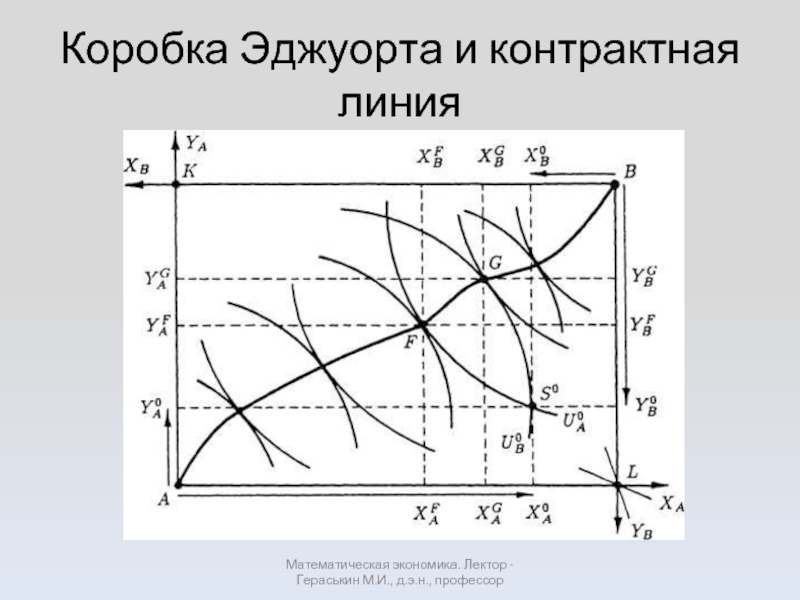
- 17. Коробка Эджуорта и контрактная линия Математическая экономика. Лектор - Гераськин М.И., д.э.н., профессор
- 18. Контрактная линия Математическая экономика. Лектор -
- 19. Пример вывода выражения контрактной линии Математическая
- 20. Обозначив запишем
- 21. Рассмотрим частный случай потребителей, имеющих противоположные предпочтения
- 22. Таким образом, контрактная линия является монотонно возрастающей
- 23. Условия максимизации полезности Математическая экономика. Лектор
- 24. Пример определения равновесия в обмене Математическая
- 25. и заменив коэффициенты эластичности α на γ,
- 26. 5.4. РАВНОВЕСИЕ В ПРОИЗВОДСТВЕ. ДВУХФАКТОРНАЯ ДВУХПРОДУКТОВАЯ
- 27. Уравнение контрактной линии при обмене производственными ресурсами
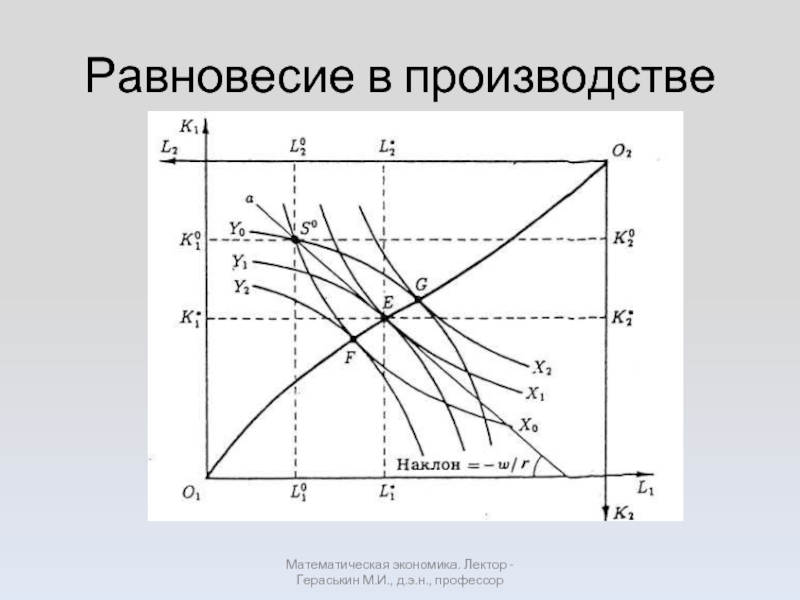
- 28. Равновесие в производстве Математическая экономика. Лектор - Гераськин М.И., д.э.н., профессор
- 29. 5.5. РАВНОВЕСИЕ В ПРОИЗВОДСТВЕ И ПОТРЕБЛЕНИИ Математическая экономика. Лектор - Гераськин М.И., д.э.н., профессор
- 30. Кривая производственных возможностей (кривая продуктовой трансформации) характеризует
- 31. Пример вывода формулы кривой производственных возможностей
- 32. Кривая производственных возможностей является эллиптической кривой, то
- 33. Предельная норма продуктовой трансформации (MRPT; marginal rate
- 34. Можно показать, что предельная норма продуктовой трансформации
- 35. Отсюда: Математическая экономика. Лектор - Гераськин
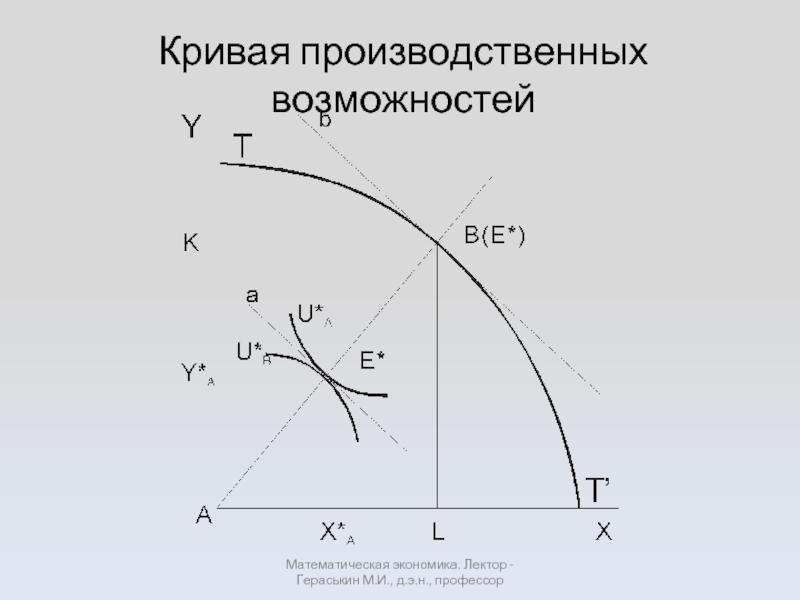
- 36. Кривая производственных возможностей Математическая экономика. Лектор - Гераськин М.И., д.э.н., профессор
- 37. Таким образом, в условиях совершенной конкуренции двух-субъектная,
- 38. 5.6. МОДЕЛЬ ОБЩЕГО РАВНОВЕСИЯ ВАЛЬРАСА Математическая экономика. Лектор - Гераськин М.И., д.э.н., профессор
- 39. Функция спроса на товар является функцией цен
- 40. Функция избыточного спроса (ED; excess demand —
- 41. Кривая избыточного спроса Математическая экономика. Лектор - Гераськин М.И., д.э.н., профессор
- 42. Условие «расчистки рынка» - для экономики в
- 43. Разделим все цены на Р1. Тогда (5.21)
- 44. Пример условий равновесия для линейных функций спроса
- 45. Для рынка двух товаров условие (5.20) имеет
- 46. Приняв цену первого товара в качестве единицы
Слайд 1Математическая экономика
Тема 5. ОБЩЕЕ РАВНОВЕСИЕ
Математическая экономика. Лектор - Гераськин М.И., д.э.н.,
Слайд 25.1. ВИДЫ И ОБЪЕКТЫ РАВНОВЕСНЫХ МОДЕЛЕЙ
Математическая экономика. Лектор - Гераськин М.И.,
Слайд 3Равновесные модели подразделяются на модели: - частичного, - полирынкового (англ. multi-market) -
Математическая экономика. Лектор - Гераськин М.И., д.э.н., профессор
Слайд 4Круговые потоки в двухсекторной экономике
Математическая экономика. Лектор - Гераськин М.И., д.э.н.,
Слайд 55.2. ПРОСТОЙ ОБМЕН В ДВУХСУБЪЕКТНОЙ ДВУХПРОДУКТОВОЙ ЭКОНОМИКЕ
Математическая экономика. Лектор -
Слайд 6Экономика состоит из двух субъектов, А и В, изначально имеющих два
Математическая экономика. Лектор - Гераськин М.И., д.э.н., профессор
Кривая предложения из запаса
Бюджетное уравнение для одного из субъектов :
(5.1)
где I – бюджет субъекта А;
px и py – цены (идеальные) товаров.
Слайд 7Кривая предложения ОСA товара Y из его начального запаса Y0А к
Математическая экономика. Лектор - Гераськин М.И., д.э.н., профессор
Слайд 8Экономически кривая предложения из запаса показывает количество второго товара, до которого
Математическая экономика. Лектор - Гераськин М.И., д.э.н., профессор
Слайд 9Получим выражение кривой предложения из запаса, учитывая, что для неё, во-первых,
Математическая экономика. Лектор - Гераськин М.И., д.э.н., профессор
(5.2)
и, во-вторых, она соединяет бюджетные линии, проходящие через некоторую точку:
(5.3)
Слайд 10Выразив соотношение цен товаров из (5.3),
Математическая экономика. Лектор - Гераськин М.И., д.э.н., профессор
(5.4)
Слайд 11Кривые предложения двух субъектов
Математическая экономика. Лектор - Гераськин М.И., д.э.н., профессор
Слайд 12Пример вывода выражения кривой предложения
Математическая экономика. Лектор - Гераськин М.И., д.э.н.,
Например, для степенной функции полезности вида
имеем следующее выражение кривой предложения:
откуда
следовательно
Слайд 13Это уравнение определяет гиперболу, вертикальная асимптота (нуль знаменателя) которой имеет координату:
Математическая экономика. Лектор - Гераськин М.И., д.э.н., профессор
Слайд 14При этом предполагается, что
Математическая экономика. Лектор - Гераськин М.И., д.э.н., профессор
Слайд 155.3. АНАЛИЗ ОБМЕНА В ДВУХСУБЪЕКТНОЙ ДВУХПРОДУКТОВОЙ ЭКОНОМИКЕ.
КОРОБКА ЭДЖУОРТА
Математическая экономика. Лектор
Слайд 16Коробка Эджуорта представляет совмещенные карты безразличия двух субъектов, А и В,
Математическая экономика. Лектор - Гераськин М.И., д.э.н., профессор
Слайд 17Коробка Эджуорта и контрактная линия
Математическая экономика. Лектор - Гераськин М.И., д.э.н.,
Слайд 18Контрактная линия
Математическая экономика. Лектор - Гераськин М.И., д.э.н., профессор
Множество точек касания
Уравнение контрактной линии имеет вид:
(5.6)
Слайд 19Пример вывода выражения контрактной линии
Математическая экономика. Лектор - Гераськин М.И., д.э.н.,
Для степенных функций полезности субъектов
имеем следующее выражение контрактной линии:
, откуда
следовательно
Слайд 20Обозначив запишем это уравнение в виде:
Математическая
Это уравнение определяет семейство функций Y=Y(X). Преобразуя к квадрату разности левую и правую части уравнения, получим:
(5.7)
Слайд 21Рассмотрим частный случай потребителей, имеющих противоположные предпочтения
Математическая экономика. Лектор - Гераськин М.И., д.э.н., профессор
Для случая равенства запасов K=L имеем:
(5.8)
Слайд 22Таким образом, контрактная линия является монотонно возрастающей (для степенных функций полезности
Математическая экономика. Лектор - Гераськин М.И., д.э.н., профессор
Слайд 23Условия максимизации полезности
Математическая экономика. Лектор - Гераськин М.И., д.э.н., профессор
Максимальное удовлетворение
(5.9)
Слайд 24Пример определения равновесия в обмене
Математическая экономика. Лектор - Гераськин М.И., д.э.н.,
Выражение кривой предложения первого субъекта
получено выше (формула (5.5)). Выражение кривой предложения второго субъекта найдем, подставив в эту формулу координаты второй системы осей в коробке Эджуорта
Слайд 25и заменив коэффициенты эластичности α на γ, β на δ. В
Математическая экономика. Лектор - Гераськин М.И., д.э.н., профессор
Координаты точки равновесия определяем, приравнивая выражение кривой предложения первого субъекта и второго субъекта откуда
(5.10)
Полученное трансцендентное уравнение позволяет определить искомый оптимальный товарный набор.
Слайд 265.4. РАВНОВЕСИЕ В ПРОИЗВОДСТВЕ.
ДВУХФАКТОРНАЯ ДВУХПРОДУКТОВАЯ МОДЕЛЬ
Математическая экономика. Лектор -
Слайд 27Уравнение контрактной линии при обмене производственными ресурсами имеет вид:
Математическая экономика. Лектор
MRTSXKL = MRTSYKL . (5.11)
Равновесие при обмене производственными ресурсами устанавливается при условии:
(5.12)
где обозначены фактора производства, К и L, приобретаемых по ценам w и r.
Слайд 28Равновесие в производстве
Математическая экономика. Лектор - Гераськин М.И., д.э.н., профессор
Слайд 295.5. РАВНОВЕСИЕ В ПРОИЗВОДСТВЕ И ПОТРЕБЛЕНИИ
Математическая экономика. Лектор - Гераськин М.И.,
Слайд 30Кривая производственных возможностей (кривая продуктовой трансформации) характеризует все множество комбинаций максимальных
Математическая экономика. Лектор - Гераськин М.И., д.э.н., профессор
Слайд 31Пример вывода формулы кривой производственных возможностей
Математическая экономика. Лектор - Гераськин М.И.,
Для производственных функций фирм
можно получить выражение кривой производственных возможностей, если один из ресурсов, например К, расходуется на выпуск обоих продуктов:
(5.13)
Слайд 32Кривая производственных возможностей является эллиптической кривой, то есть прирост производства одного
Математическая экономика. Лектор - Гераськин М.И., д.э.н., профессор
Слайд 33Предельная норма продуктовой трансформации (MRPT; marginal rate of product transformation —
Математическая экономика. Лектор - Гераськин М.И., д.э.н., профессор
MRPTХY = –
Слайд 34Можно показать, что предельная норма продуктовой трансформации равна соотношению предельных издержек
Математическая экономика. Лектор - Гераськин М.И., д.э.н., профессор
MRPTХY = –
=
(5.14)
Действительно, при постоянных запасах ресурсов
дифференциал издержек равен нулю:
Слайд 35Отсюда:
Математическая экономика. Лектор - Гераськин М.И., д.э.н., профессор
В условиях совершенной конкуренции
MRPTХY =
=
(5.15)
Поскольку правые части (5.15) и (5.9) одинаковы — PX/PY, мы можем приравнять и левые их части, в результате чего получим условие общего равновесия:
MRPTХY = MRSAX,Y = MRSBX,Y .
Слайд 36Кривая производственных возможностей
Математическая экономика. Лектор - Гераськин М.И., д.э.н., профессор
Слайд 37Таким образом, в условиях совершенной конкуренции двух-субъектная, двухфакторная, двухпродуктовая экономическая система
Математическая экономика. Лектор - Гераськин М.И., д.э.н., профессор
Слайд 385.6. МОДЕЛЬ ОБЩЕГО РАВНОВЕСИЯ ВАЛЬРАСА
Математическая экономика. Лектор - Гераськин М.И., д.э.н.,
Слайд 39Функция спроса на товар является функцией цен всех т товаров:
Математическая
QDi=Di(P1,...,Pi,...,Pm), i=1,2,...,т. (5.17)
На совершенно конкурентном рынке предложение товара также является функцией цен всех т товаров:
QSi=Si(P1,...,Pi,...,Pm), i = 1,2,.:,m. (5.18)
Слайд 40Функция избыточного спроса (ED; excess demand — англ.) на товар может
Математическая экономика. Лектор - Гераськин М.И., д.э.н., профессор
EDi(P1,…Pi,…Pm)= Di(P1,...P,i...Pm)-Si(Pl,...,Pi,...,Pm). (5.19)
Условием равновесия на рынках – равенство избыточного спроса нулю:
EDi (P1,...,Pm) = 0. (5.20)
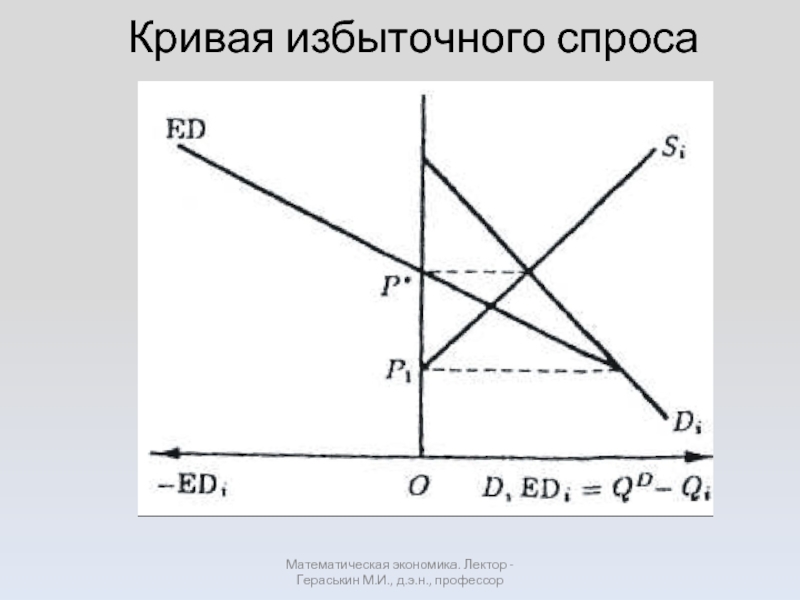
Слайд 41Кривая избыточного спроса
Математическая экономика. Лектор - Гераськин М.И., д.э.н., профессор
Слайд 42Условие «расчистки рынка» - для экономики в целом общая ценность покупок
Математическая экономика. Лектор - Гераськин М.И., д.э.н., профессор
(5.21)
Равенство (5.21) интерпретируют обычно как закон Вальраса: если все рынки, кроме одного, т. е. т-1 рынков, находятся в равновесии, то и оставшийся (т-1)-й рынок также находится в равновесии. А это значит, что число независимых уравнений в системе равно т - 1.
Слайд 43Разделим все цены на Р1. Тогда (5.21) примет вид
Математическая экономика. Лектор
(5.22)
Таким образом, мы получили систему, состоящую из т – 1 уравнения, допускающую единственное решение относительно (т - 1 )-й цены.
Слайд 44Пример условий равновесия для линейных функций спроса и предложения
Математическая экономика. Лектор
При функциях спроса и предложения
QD =A-aP и QS =В + bР
функцией избыточного спроса будет
ЕQ =(А-В)-(а + b)Р.
Слайд 45Для рынка двух товаров условие (5.20) имеет вид:
Математическая экономика. Лектор -
откуда, разделив первое уравнение на второе, получим
Слайд 46Приняв цену первого товара в качестве единицы счета, обозначим
Математическая экономика. Лектор
Поэтому можно записать уравнение Вальраса (5.22):
(5.23)
Условие «расчистки рынка» (5.21) имеет следующий вид:
Уравнения (5.23), (5.24) позволяют найти искомые цены товаров.