- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Локальные степени вершин графа презентация
Содержание
- 1. Локальные степени вершин графа
- 2. Локальные степени вершин
- 3. Локальные степени вершин
- 4. Локальные степени вершин
- 5. Локальные степени вершин
- 6. Локальные степени вершин
- 7. Локальные степени вершин
- 8. Локальные степени вершин
- 9. Локальные степени вершин
- 10. Локальные степени вершин
- 11. Локальные степени вершин
- 12. Локальные степени вершин
- 13. Локальные степени вершин
- 14. Локальные степени вершин
- 15. Локальные степени вершин ор-графа
- 16. Локальные степени вершин
- 18. Локальные степени вершин
- 19. Локальные степени вершин
- 20. Локальные степени вершин
Слайд 2
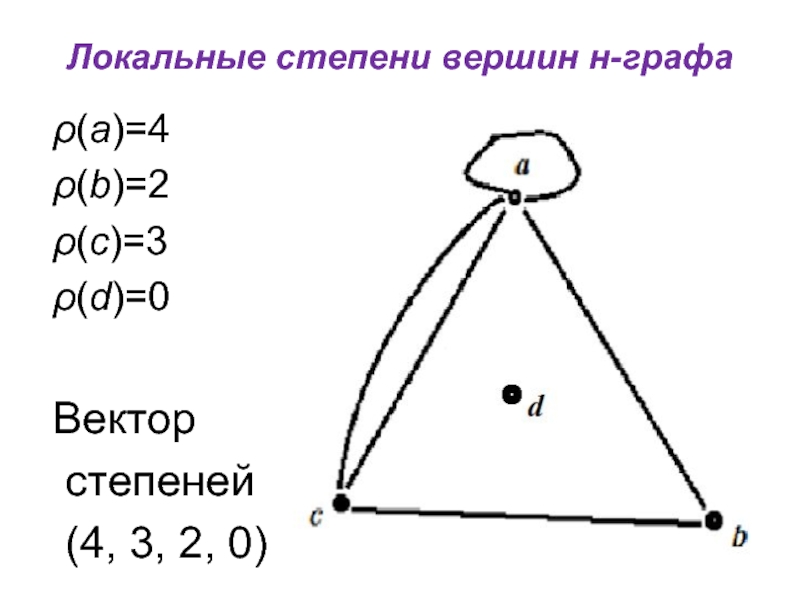
Локальные степени вершин н-графа
Пусть G =(V, E) – н-граф.
Локальной степенью вершины
называется число равное числу ребер, инцидентных вершине v. При этом вклад петли в степень
вершины равен 2.
вершины равен 2.
Слайд 3
Локальные степени вершин н-графа
Вектор степеней н-графа
G =(V, E) – вектор
размерности
n, составленный из степеней вершин графа, расположенных по убыванию.
n, составленный из степеней вершин графа, расположенных по убыванию.
Слайд 5
Локальные степени вершин н-графа
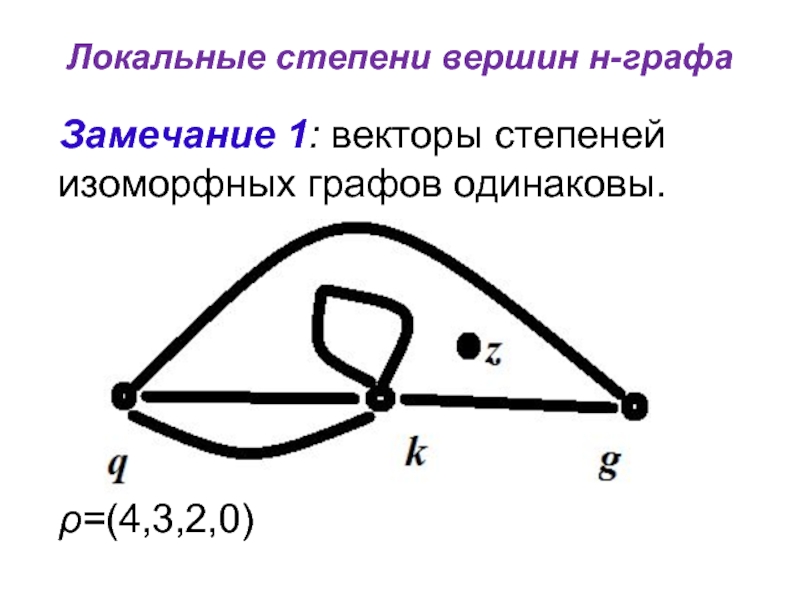
Замечание 1: векторы степеней изоморфных графов одинаковы.
ρ=(4,3,2,0)
Слайд 6
Локальные степени вершин н-графа
Замечание 2: Сумма всех локальных степеней вершин
н-графа
равна удвоенному количеству ребер.
- число ребер н-графа.
- число ребер н-графа.
Слайд 7
Локальные степени вершин н-графа
Теорема (о числе вершин нечетной степени):
Число вершин нечетной
степени – четно.
Слайд 8
Локальные степени вершин н-графа
Доказательство:
Сумма в левой части равенства – четна.
Если убрать все четные слагаемые, сумма останется четной.
Сумма нечетных слагаемых четна, если их четное число.
Слайд 9
Локальные степени вершин н-графа
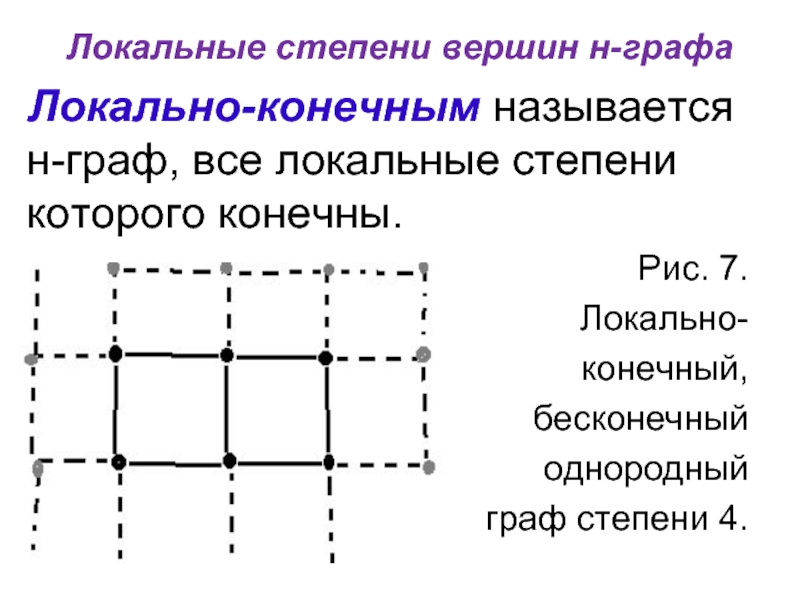
Локально-конечным называется н-граф, все локальные степени которого конечны.
Рис. 7.
Локально-
конечный,
бесконечный
однородный
граф степени 4.
Слайд 10
Локальные степени вершин н-графа
Однородным степени k называется н-граф, локальные степени которого
одинаковы и равны k.
Для однородного графа степени k:
Для однородного графа степени k:
Слайд 11
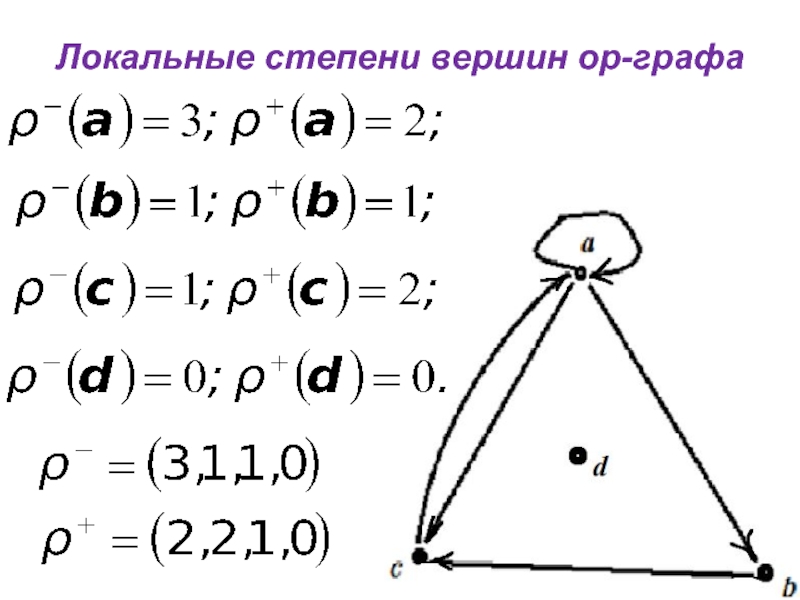
Локальные степени вершин ор-графа
Пусть G = (V, E) – ор-граф.
Локальной степенью
исхода вершины называется число , равное числу ребер, выходящих из вершины v.
Слайд 12
Локальные степени вершин ор-графа
Локальной степенью захода вершины
называется число , равное числу ребер, выходящих из вершины v.
Слайд 13
Локальные степени вершин ор-графа
Вектор степеней исхода
ор-графа G =(V, E) –
вектор размерности n, составленный из степеней исхода вершин графа, расположенных по убыванию.
Слайд 14
Локальные степени вершин ор-графа
Вектор степеней захода
ор-графа – вектор размерности n,
составленный из степеней захода вершин графа, расположенных по убыванию.
Слайд 16
Локальные степени вершин ор-графа
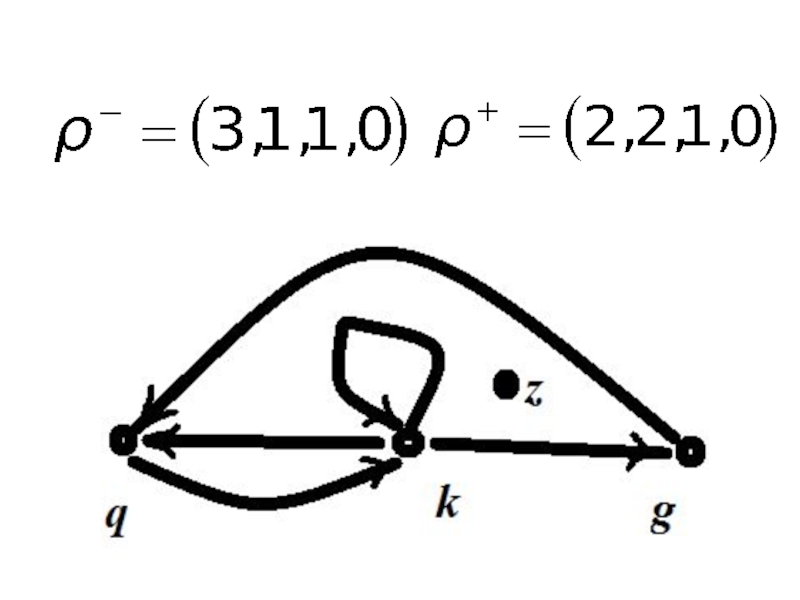
Замечание 3: векторы степеней исхода и степеней захода
изоморфных графов одинаковы.
Слайд 18
Локальные степени вершин н-графа
Замечание 4: Сумма всех локальных степеней исхода вершин
и сумма всех локальных степеней захода ор-графа равна количеству ребер.
Слайд 19
Локальные степени вершин ор-графа
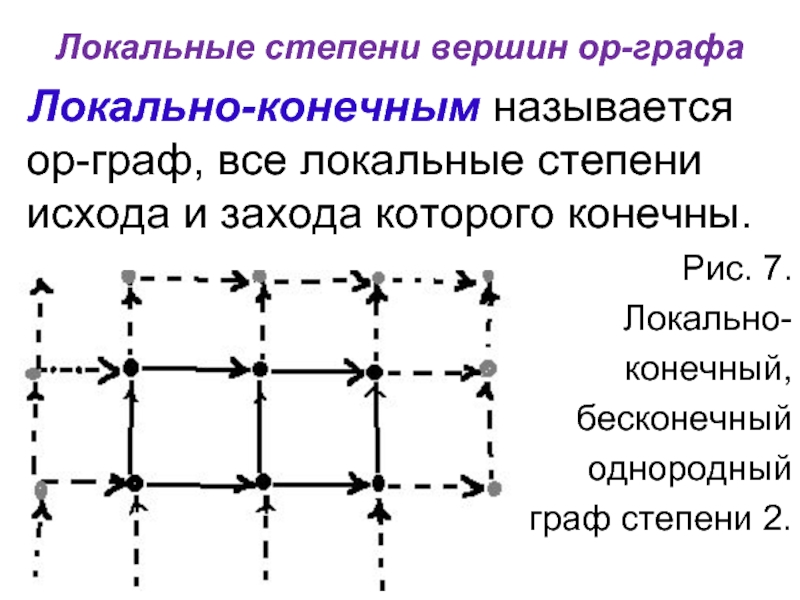
Локально-конечным называется ор-граф, все локальные степени исхода и
захода которого конечны.
Рис. 7.
Локально-
конечный,
бесконечный
однородный
граф степени 2.
Рис. 7.
Локально-
конечный,
бесконечный
однородный
граф степени 2.
Слайд 20
Локальные степени вершин ор-графа
Однородным степени k называется ор-граф, локальные степени исхода
и степени захода которого одинаковы и равны k.
Для однородного графа степени k:
Для однородного графа степени k: