- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Логика реляционная. Понятие реляционной модели презентация
Содержание
- 1. Логика реляционная. Понятие реляционной модели
- 2. Понятие реляционной модели А:=«Иванов учится в КГТУ»,
- 3. Определения РЛ атрибут (Аi) – имя столбца
- 4. Схема связи между таблицей, отношением и файлом
- 5. Структура операций над отношениями традиционные операции над
- 6. Языки управления БД языки реляционной алгебры (РА)
- 7. Реляционная алгебра
- 8. Предметный язык РЛ Алфавит Т: отношения из
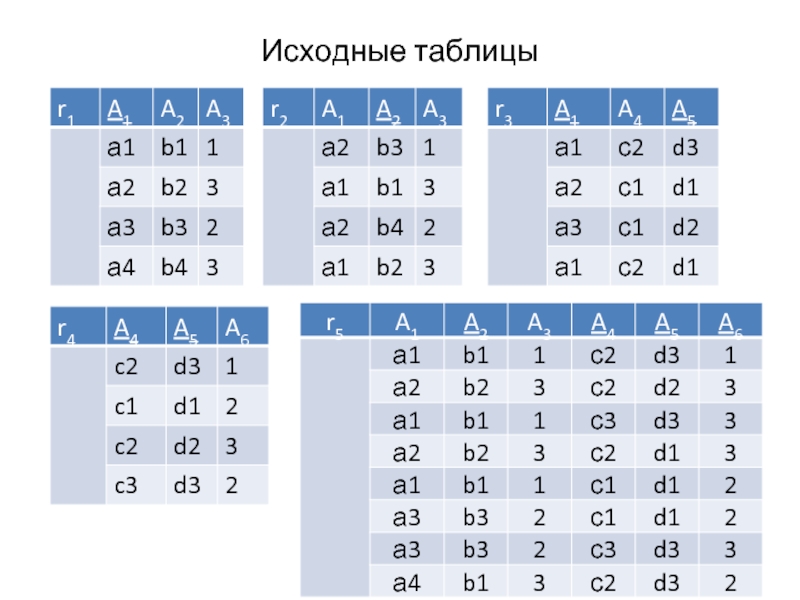
- 9. Исходные таблицы
- 10. Оператор выбора δ(r) r’=δ(r,B)={t’|t’⊆r,B,rel(r’)=rel(r)} Правила записи
- 11. Примеры использования оператора выбора 1. Дано:
- 12. 2. Дано: Выбрать
- 13. 3. Дано:
- 14. Оператор проекции πrel(r) r’=πAi, Aj, …,Ak(r)={t’|rel(r’)=Ai, Aj,
- 15. Примеры использования оператора проекции 1. Дано:
- 16. 2. Дано: Выбрать только ключи отношения r3: r'= πA1,A5(r3)={t’|rel(r’)=(A1, A5)} Результат:
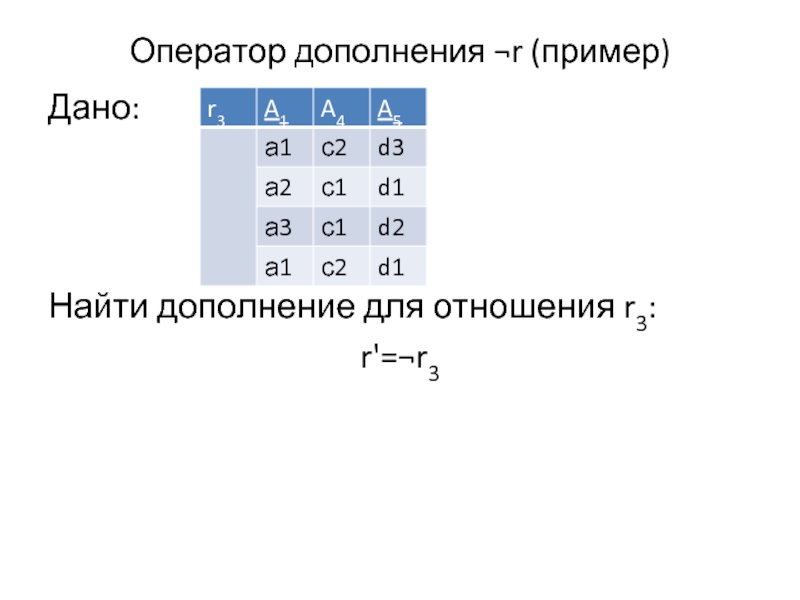
- 17. Оператор дополнения ¬r (пример) Дано:
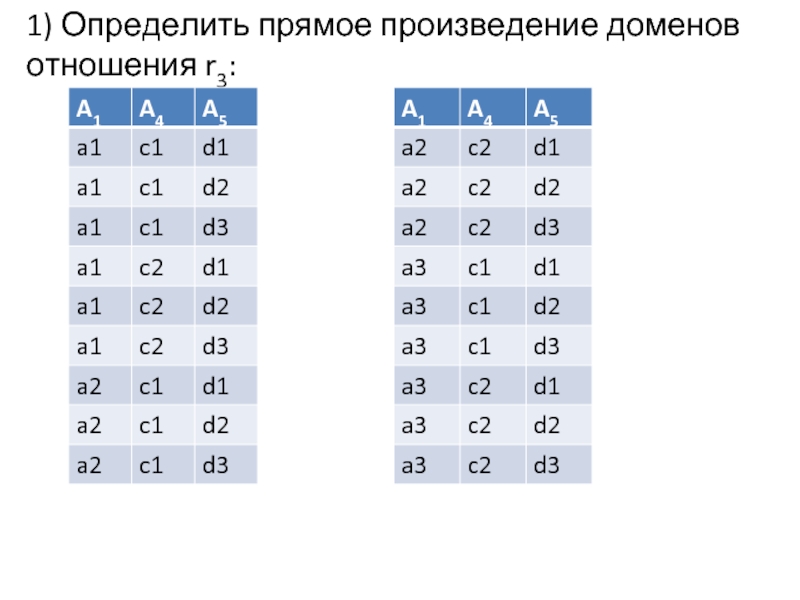
- 18. 1) Определить прямое произведение доменов отношения r3:
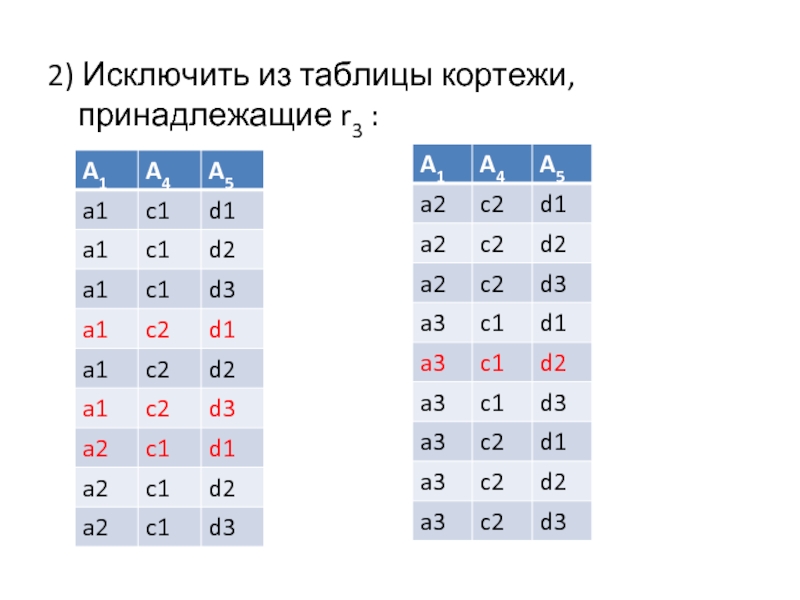
- 19. 2) Исключить из таблицы кортежи, принадлежащие r3 :
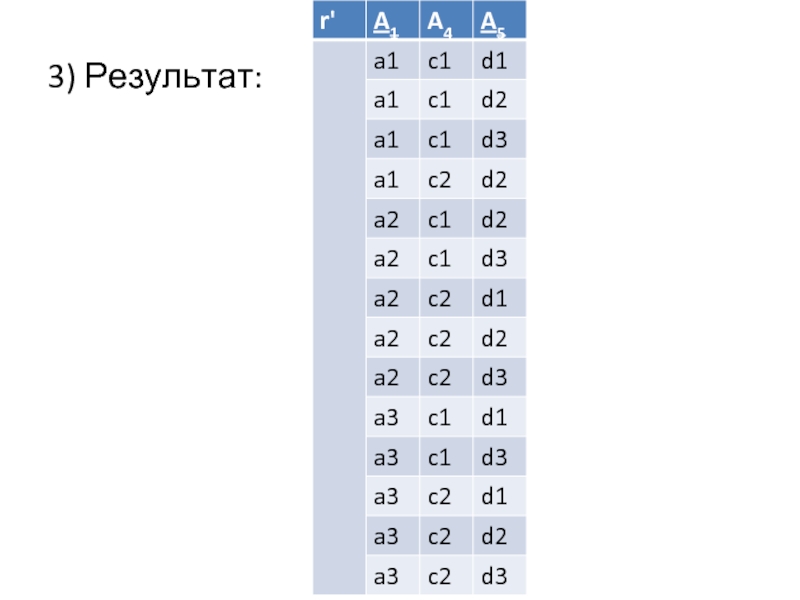
- 20. 3) Результат:
- 21. Оператор объединения ∪(r1,r2) r’=∪(r1,r2)={t’|t’=t1∈r1 или t'=t2∈r2, rel(r’)=rel(r1)=rel(r2)}
- 22. Пример оператора объединения Дано:
- 23. Оператор прямого произведения ⊗(r1,r2) r`=⊗(r1,r2)={t`|t'= (t1,t2),t1∈r1 и t2∈r2, rel(r’)=(rel(r1), rel(r2))}
- 24. Пример оператора прямого произведения Дано:
- 25. Результат:
- 26. Оператор разности \(r1,r2) r’=\(r1,r2)={t’|t’=t1∈r1 и t1≠t2∈r2, rel(r')=rel(r1)=rel(r2)}
- 27. Пример оператора разности Дано: Выполнить разность \(r1,r2): r’=r1\r2={t’|t’=t1∈r1 и t1≠t2∈r2, rel(r')=rel(r1)=rel(r2)} Результат:
- 28. Оператор пересечения ∩(r1,r2) r’=∩(r1,r2)={t’|t’=t1∈r1 и t'=t2∈r2,rel(r')=rel(r1)=rel(r2)}
- 29. Пример оператора пересечения Дано:
- 30. Оператор естественного соединения >
- 31. Пример оператора естественного соединения Дано: Выполнить естественное соединение >
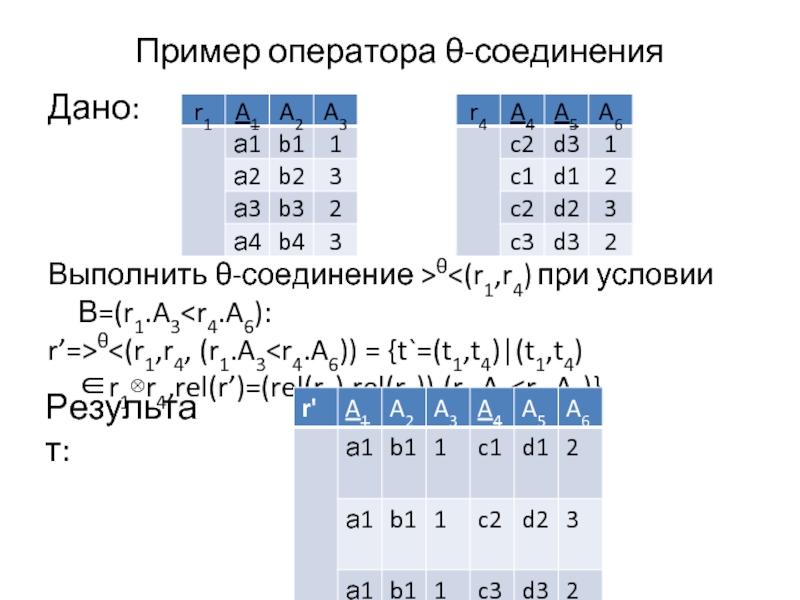
- 32. Оператор θ-соединения >θθ
- 33. Пример оператора θ-соединения Дано: Выполнить θ-соединение >θ
- 34. Оператор деления :(r1,r2) r’=:(r1,r2)={t’|t1=(t’,t2), rel(r’)=rel(r1)\rel(r2)}
- 35. Пример оператора деления Дано:
- 36. Правила реляционной алгебры r’=δB1(δB2 (r))=δB2(δB1(r)) r’=δB(r1∩r2)=δB(r1)∩δB(r2) r’=δB(r1∪r2)=δB(r1)∪δB(r2) r’=δB(r1\r2)=δB(r1)\δB(r2) r’=δB(r1>
- 37. Алгоритм реализации языка РА 1) в словесной
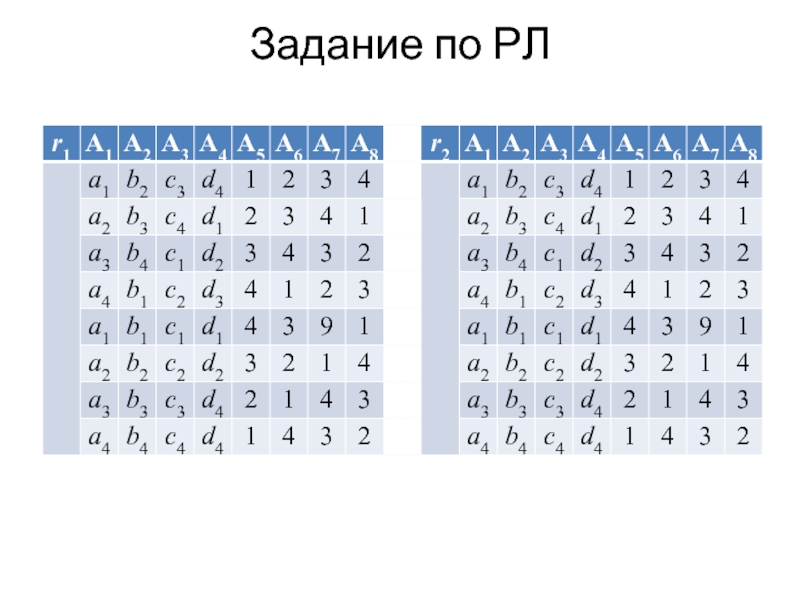
- 38. Задание по РЛ
- 39. 1) согласно варианту удалить из отношений r1
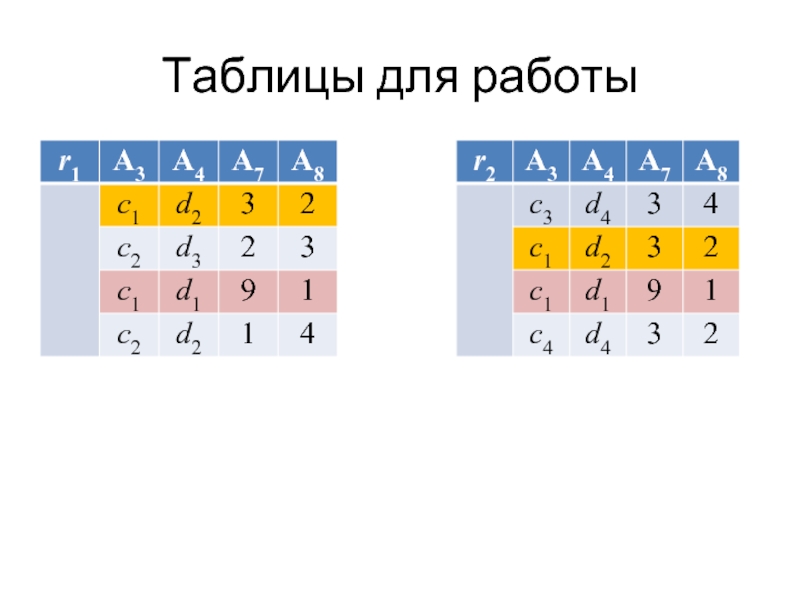
- 40. Таблицы для работы
- 41. 2) выполнить операции (r1∪r2), (r1∩r2), (r1\r2) (r1⊗r2):
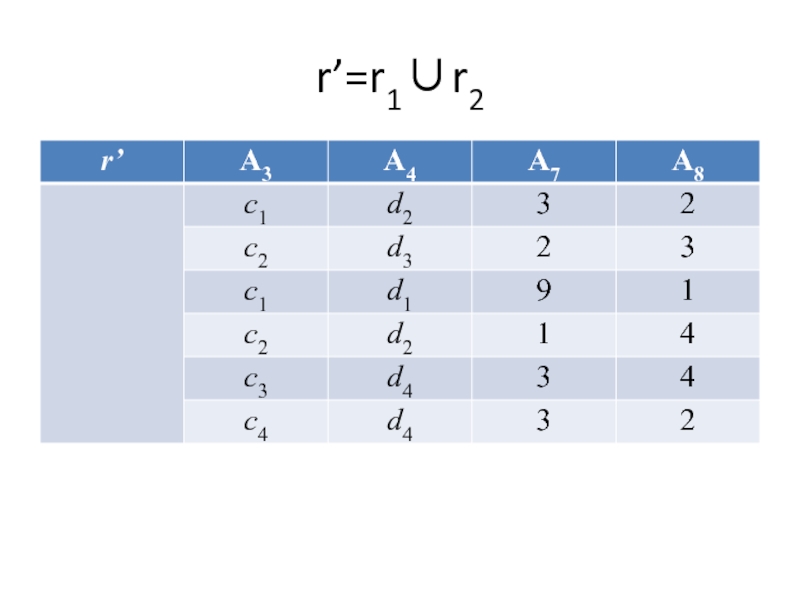
- 42. r’=r1∪r2
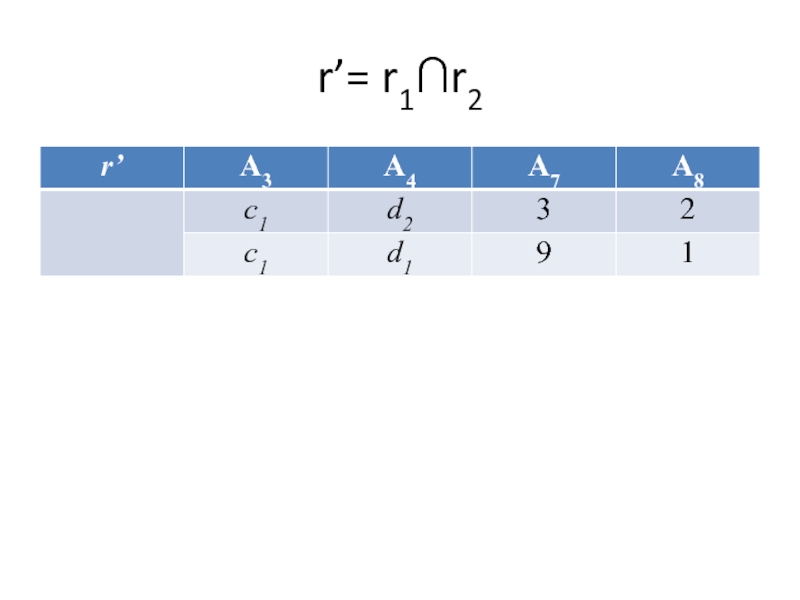
- 43. r’= r1∩r2
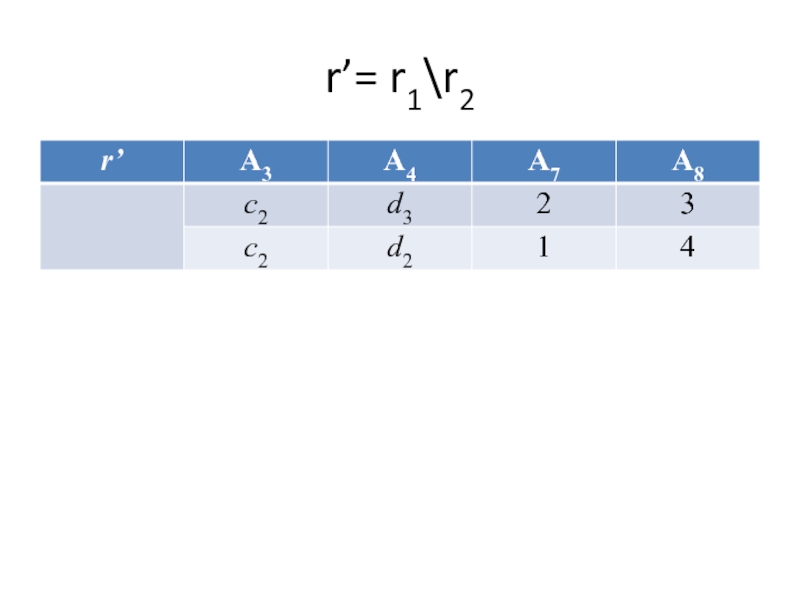
- 44. r’= r1\r2
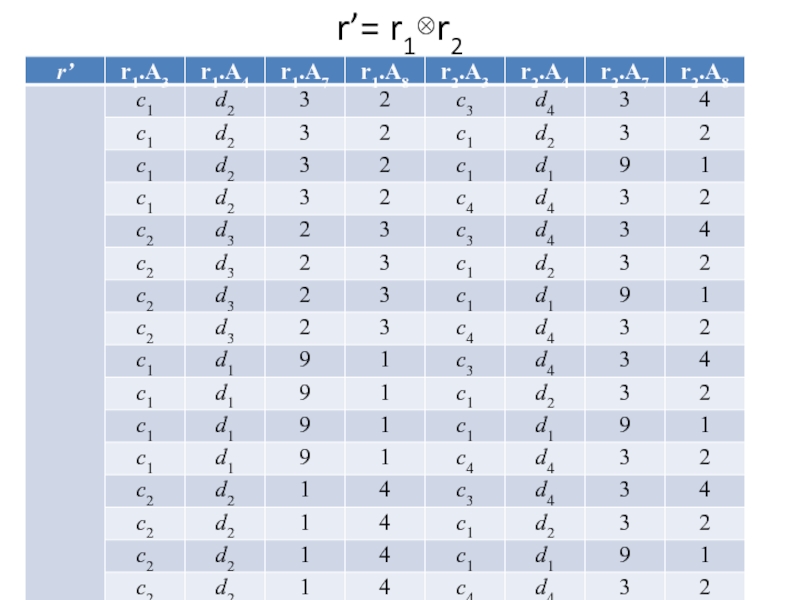
- 45. r’= r1⊗r2
- 46. 3) выполнить операции >< или >θθ
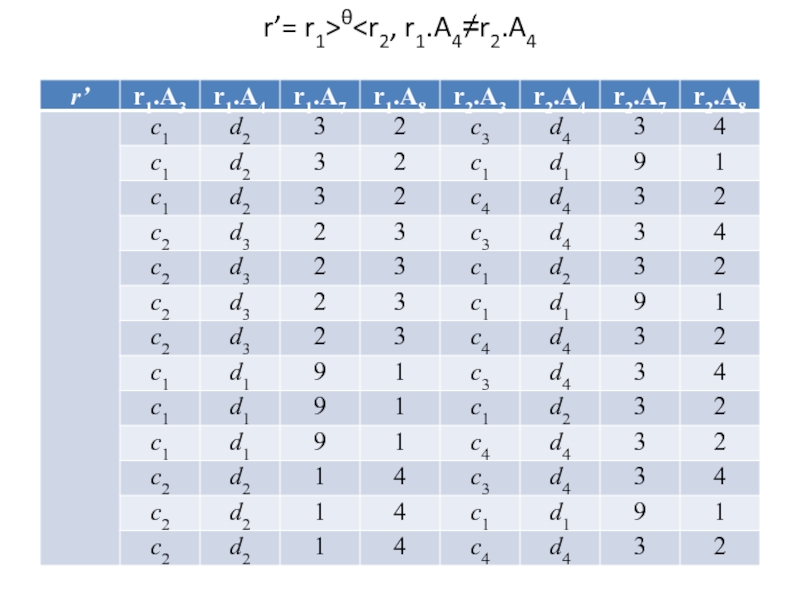
- 47. r’= r1>θ
- 48. r’’= δ(r’,r1.A3≠c1 and r2.A3≠c1)
- 49. r‘’’=πr1.A4, r2.A4, r2.A3(r’’)
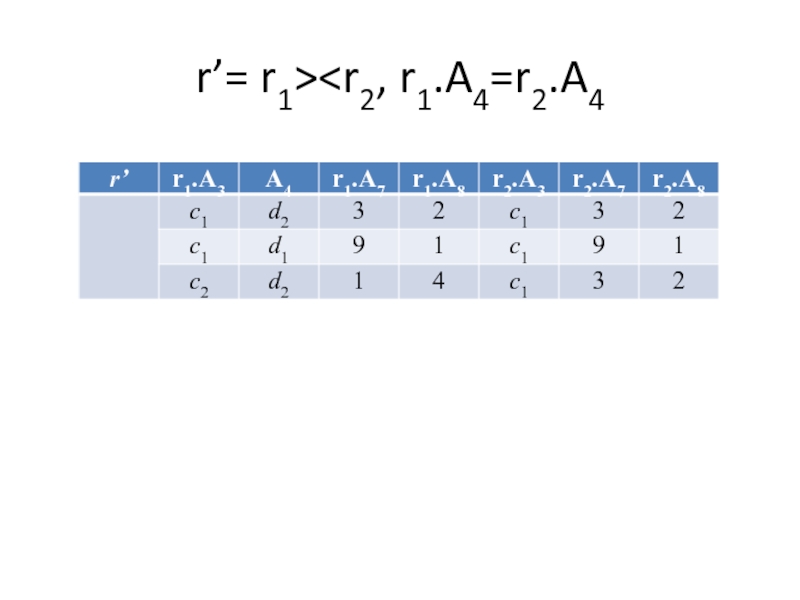
- 50. r’= r1>
- 51. r’’= δ(r’,r1.A3≠c1 or r2.A3≠c1)
- 52. r’’’=πr1.A4, r2.A7, r2.A3(r’’)
Слайд 2Понятие реляционной модели
А:=«Иванов учится в КГТУ»,
В:=«Сидоров учится в БГА»,
С:=«Петров учится в
БФУ».
Синтаксическая модель высказываний:
<фамилия>"учится"<название ВУЗа>
<фамилия> - {Иванов, Сидоров, Петров},
<название ВУЗа> - {КГТУ, БГА, БФУ}.
Реляционная модель высказываний:
r="учится"∈{<фамилия>}⊗{<название ВУЗа>}
Синтаксическая модель высказываний:
<фамилия>"учится"<название ВУЗа>
<фамилия> - {Иванов, Сидоров, Петров},
<название ВУЗа> - {КГТУ, БГА, БФУ}.
Реляционная модель высказываний:
r="учится"∈{<фамилия>}⊗{<название ВУЗа>}
Слайд 3Определения РЛ
атрибут (Аi) – имя столбца таблицы - Фамилия,
домен (Dj) -
область определения атрибута : для Название ВУЗа - {КГТУ, БГА, БФУ},
мощность - число строк таблицы,
кортеж (t)– строка таблицы, содержащая значения атрибутов - (Иванов, КГТУ). Если дано множество атрибутов A={A1,A2,…,An} и множество доменов D={D1,D2,..., Dm}, то t=(d1,d2,...,dn) где di∈Dj. Кортежи называют совместимыми, если они имеют одинаковые характеристики: число атрибутов и имена, а также их порядок в кортеже,
отношение (r) - множество совместимых кортежей, r={t| t=(d1,d2,...,dn), di∈Dj}⊆⊗nD; характеризуется схемой отношения rel(r)=(A1, A2,…, An) и арностью n,
ключ – один или несколько атрибутов, выделяющих единственный кортеж отношения,
реляционная база данных (R) - множество отношений для определенной области деятельности - R={ri}; характеризуется схемой реляционной базы данных REL(R)={rel(r)}.
мощность - число строк таблицы,
кортеж (t)– строка таблицы, содержащая значения атрибутов - (Иванов, КГТУ). Если дано множество атрибутов A={A1,A2,…,An} и множество доменов D={D1,D2,..., Dm}, то t=(d1,d2,...,dn) где di∈Dj. Кортежи называют совместимыми, если они имеют одинаковые характеристики: число атрибутов и имена, а также их порядок в кортеже,
отношение (r) - множество совместимых кортежей, r={t| t=(d1,d2,...,dn), di∈Dj}⊆⊗nD; характеризуется схемой отношения rel(r)=(A1, A2,…, An) и арностью n,
ключ – один или несколько атрибутов, выделяющих единственный кортеж отношения,
реляционная база данных (R) - множество отношений для определенной области деятельности - R={ri}; характеризуется схемой реляционной базы данных REL(R)={rel(r)}.
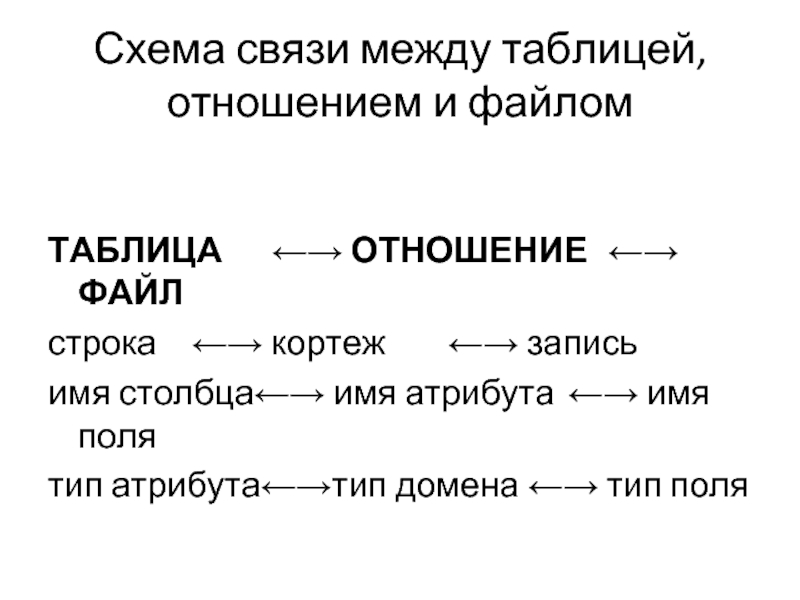
Слайд 4Схема связи между таблицей, отношением и файлом
ТАБЛИЦА ←→
ОТНОШЕНИЕ ←→ ФАЙЛ
строка ←→ кортеж ←→ запись
имя столбца←→ имя атрибута ←→ имя поля
тип атрибута←→тип домена ←→ тип поля
строка ←→ кортеж ←→ запись
имя столбца←→ имя атрибута ←→ имя поля
тип атрибута←→тип домена ←→ тип поля
Слайд 5Структура операций над отношениями
традиционные операции над множествами: дополнение, объединение, пересечение, разность,
декартово произведение, деление;
специальные реляционные операции: проекция, соединение и выбор.
специальные реляционные операции: проекция, соединение и выбор.
Слайд 6Языки управления БД
языки реляционной алгебры (РА) - описывают последовательность действий для
получения желаемого результата - процедурные языки,
языки реляционного исчисления (РИ) - предоставляют пользователю набор правил для записи запросов к БД, в которых содержится только информация о желаемом результате. Пример - язык запросов SQL (Structured Query Language).
языки реляционного исчисления (РИ) - предоставляют пользователю набор правил для записи запросов к БД, в которых содержится только информация о желаемом результате. Пример - язык запросов SQL (Structured Query Language).
Слайд 8Предметный язык РЛ
Алфавит Т:
отношения из множества {r1,r2,…},
операторы над отношениями:
∪-
объединение,
∩- пересечение,
\ - разность,
⊗ - прямое произведение,
¬ - дополнение,
δ(r,B) - выбор кортежа из отношения r по условию B,
πrel(r) - проекция отношения r на схему rel,
>< - естественное соединение,
>θ< - θ-соединение,
: - деление,
логические операторы {&,∨,¬},
операторы сравнения {=, ≠, >, ≥, <, ≤},
арифметические операторы {+, -, *, /}
кванторы {∃, ∀},
круглые скобки и запятая.
∩- пересечение,
\ - разность,
⊗ - прямое произведение,
¬ - дополнение,
δ(r,B) - выбор кортежа из отношения r по условию B,
πrel(r) - проекция отношения r на схему rel,
>< - естественное соединение,
>θ< - θ-соединение,
: - деление,
логические операторы {&,∨,¬},
операторы сравнения {=, ≠, >, ≥, <, ≤},
арифметические операторы {+, -, *, /}
кванторы {∃, ∀},
круглые скобки и запятая.
Слайд 10Оператор выбора δ(r)
r’=δ(r,B)={t’|t’⊆r,B,rel(r’)=rel(r)}
Правила записи условия В:
простое условие: B=Аiθki, где θ∈{=,
≠, >, ≥, <, ≤}, kj∈Dj,
2) условие:
простое условие – условие,
если В – условие, то ¬B – условие,
если В1 и В2 – условия, то B1&B2, B1∨B2 – условия.
2) условие:
простое условие – условие,
если В – условие, то ¬B – условие,
если В1 и В2 – условия, то B1&B2, B1∨B2 – условия.
Слайд 11Примеры использования оператора выбора
1. Дано:
Выбрать кортежи отношения r1 по значению
ключа А1=а2:
r’=δ(r1,(A1=a2))={t’|t’⊆r,(A1=a2),rel(r’)=rel(r1)}
Результат:
r’=δ(r1,(A1=a2))={t’|t’⊆r,(A1=a2),rel(r’)=rel(r1)}
Результат:
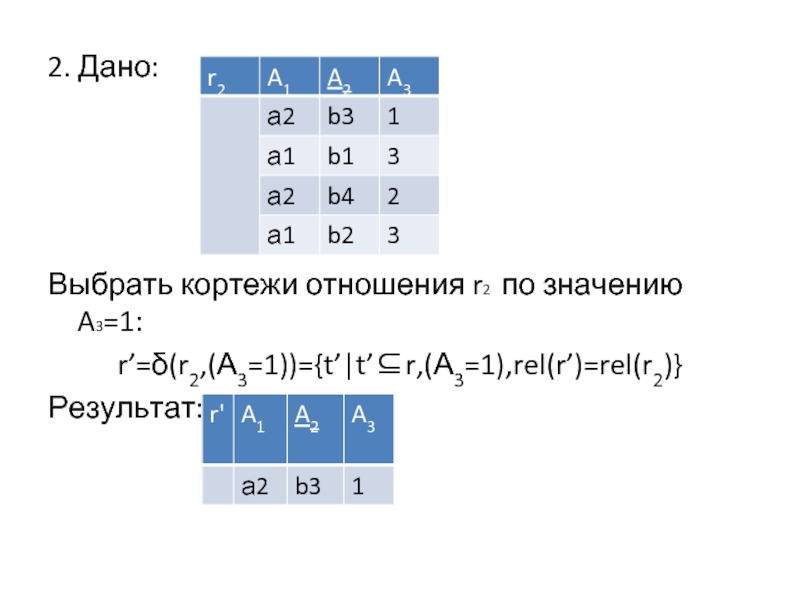
Слайд 122. Дано:
Выбрать кортежи отношения r2 по значению A3=1:
r’=δ(r2,(А3=1))={t’|t’⊆r,(А3=1),rel(r’)=rel(r2)}
Результат:
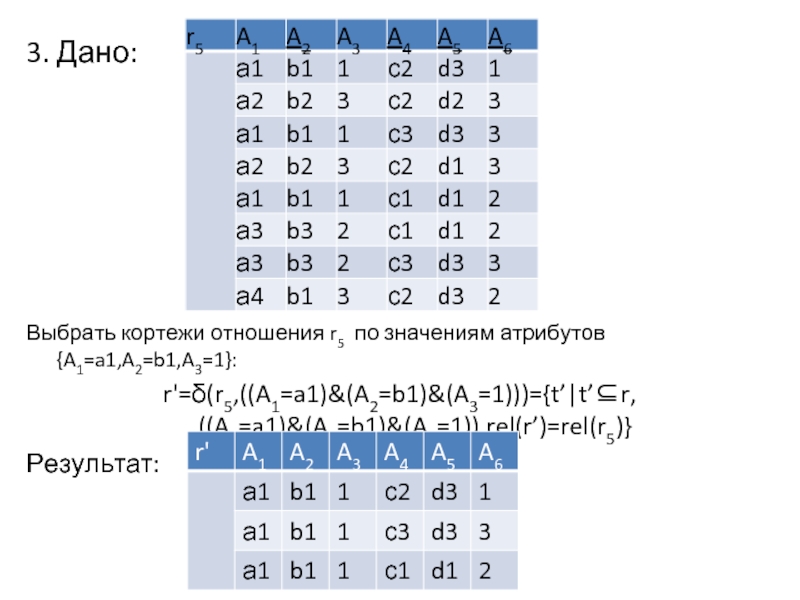
Слайд 133. Дано:
Выбрать кортежи отношения r5 по значениям атрибутов {A1=a1,A2=b1,A3=1}:
r'=δ(r5,((A1=a1)&(A2=b1)&(A3=1)))={t’|t’⊆r, ((A1=a1)&(A2=b1)&(A3=1)),rel(r’)=rel(r5)}
Результат:
Слайд 14Оператор проекции πrel(r)
r’=πAi, Aj, …,Ak(r)={t’|rel(r’)=Ai, Aj, …, Ak },
где 1 ≤
i, j, k ≤ n
Слайд 15Примеры использования оператора проекции
1. Дано:
Выбрать только ключи отношения r1:
r’=
πA1(r1)={t’|rel(r’)=(A1)}
Результат:
Результат:
Слайд 21Оператор объединения ∪(r1,r2)
r’=∪(r1,r2)={t’|t’=t1∈r1 или t'=t2∈r2, rel(r’)=rel(r1)=rel(r2)}
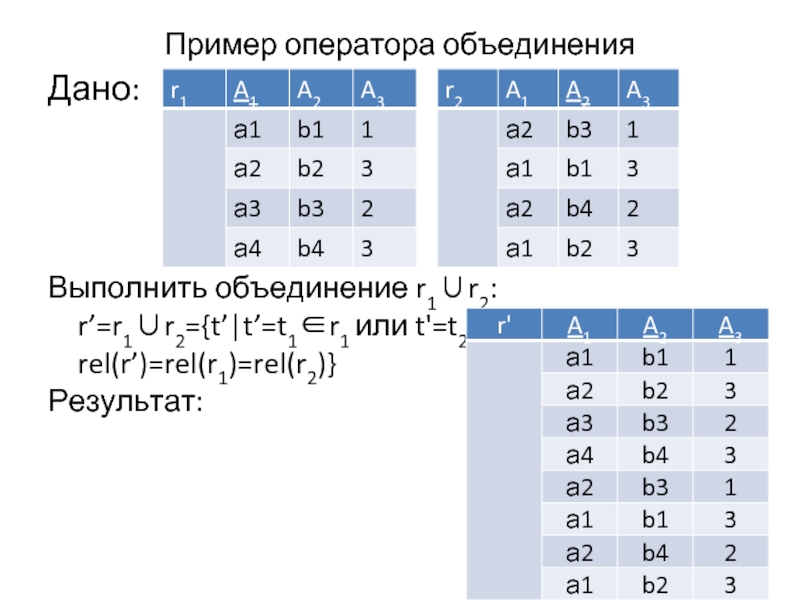
Слайд 22Пример оператора объединения
Дано:
Выполнить объединение r1∪r2: r’=r1∪r2={t’|t’=t1∈r1 или t'=t2∈r2, rel(r’)=rel(r1)=rel(r2)}
Результат:
Слайд 23Оператор прямого произведения ⊗(r1,r2)
r`=⊗(r1,r2)={t`|t'= (t1,t2),t1∈r1 и t2∈r2, rel(r’)=(rel(r1), rel(r2))}
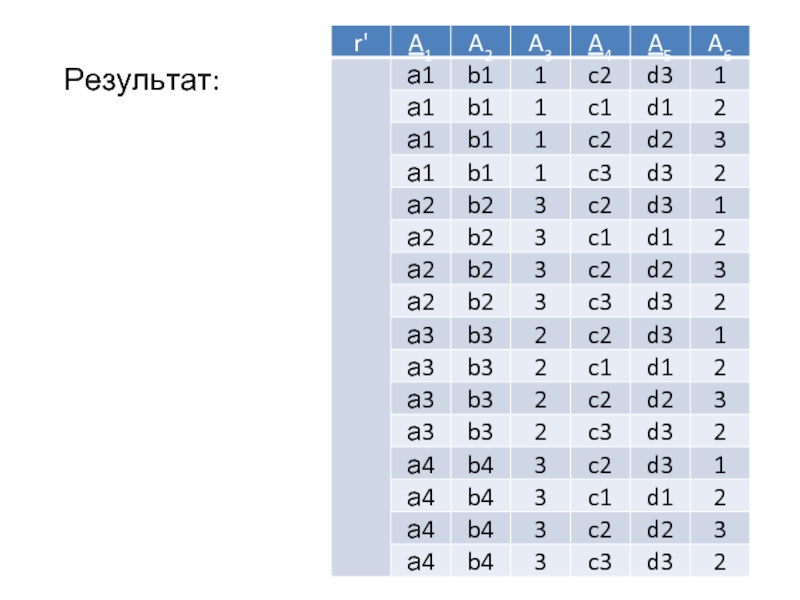
Слайд 24Пример оператора прямого произведения
Дано:
Выполнить прямое произведение ⊗(r1 ,r4): r`=r1 ⊗r4=
{t`|t‘=(t1,t4),t1∈r1
и t4∈r4, rel(r’)=(rel(r1),rel(r4))}
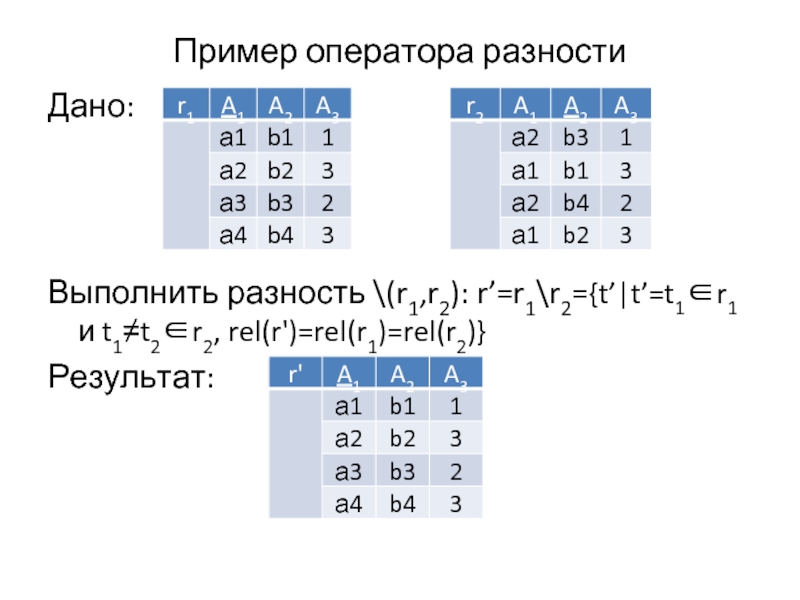
Слайд 27Пример оператора разности
Дано:
Выполнить разность \(r1,r2): r’=r1\r2={t’|t’=t1∈r1 и t1≠t2∈r2, rel(r')=rel(r1)=rel(r2)}
Результат:
Слайд 29Пример оператора пересечения
Дано:
Выполнить пересечение ∩( r1,r2): r'=r1∩r2= {t’|t’=t1∈r1 и t'=t2∈r2,rel(r')=rel(r1)=rel(r2)}
Результат:
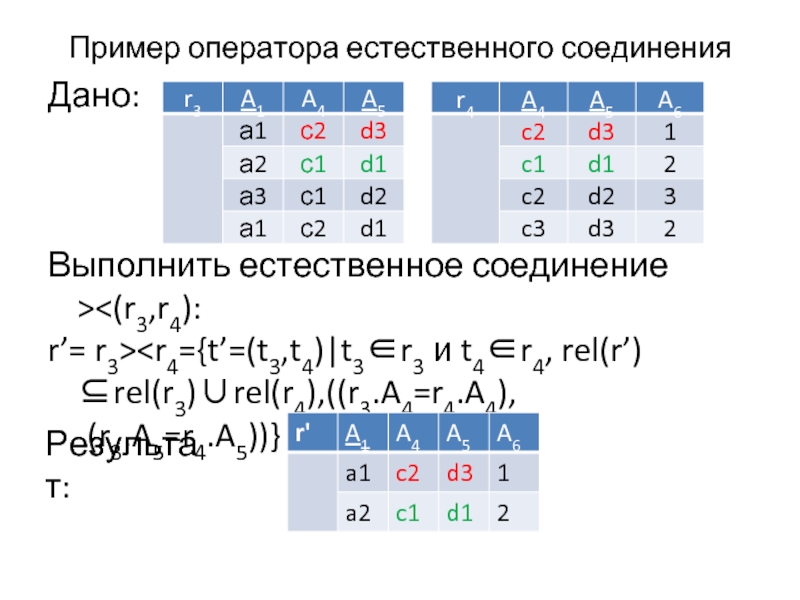
Слайд 31Пример оператора естественного соединения
Дано:
Выполнить естественное соединение >
rel(r’)⊆rel(r3)∪rel(r4),((r3.A4=r4.A4),
(r3.A5=r4.A5))}
(r3.A5=r4.A5))}
Результат:
Слайд 35Пример оператора деления
Дано:
Выполнить деление :(r5,r4): r’=:(r5,r4) ={t’|t5=(t’,t4), rel(r’)=rel(r5)\rel(r4)}
Результат:
Слайд 36Правила реляционной алгебры
r’=δB1(δB2 (r))=δB2(δB1(r))
r’=δB(r1∩r2)=δB(r1)∩δB(r2)
r’=δB(r1∪r2)=δB(r1)∪δB(r2)
r’=δB(r1\r2)=δB(r1)\δB(r2)
r’=δB(r1>
Слайд 37Алгоритм реализации языка РА
1) в словесной формулировке запроса выделяются имена атрибутов,
вход и выход запроса, а также условия выборки;
2) анализируются атрибуты:
если все атрибуты находятся в одном отношении, то последующие операции (описаны в п.3) проводятся только с ним;
если атрибуты распределены по нескольким отношениям, то эти отношения необходимо соединить в одном отношении;
3) отношение обрабатывается операциями выборки и проекции, причем выборка по значениям атрибута должна предшествовать проекции, в которой этот атрибут выводится из отношения;
4) если запрос можно разделить на части (подзапросы), то его реализация также делится на части, где результатом подзапроса является отдельное отношение.
2) анализируются атрибуты:
если все атрибуты находятся в одном отношении, то последующие операции (описаны в п.3) проводятся только с ним;
если атрибуты распределены по нескольким отношениям, то эти отношения необходимо соединить в одном отношении;
3) отношение обрабатывается операциями выборки и проекции, причем выборка по значениям атрибута должна предшествовать проекции, в которой этот атрибут выводится из отношения;
4) если запрос можно разделить на части (подзапросы), то его реализация также делится на части, где результатом подзапроса является отдельное отношение.
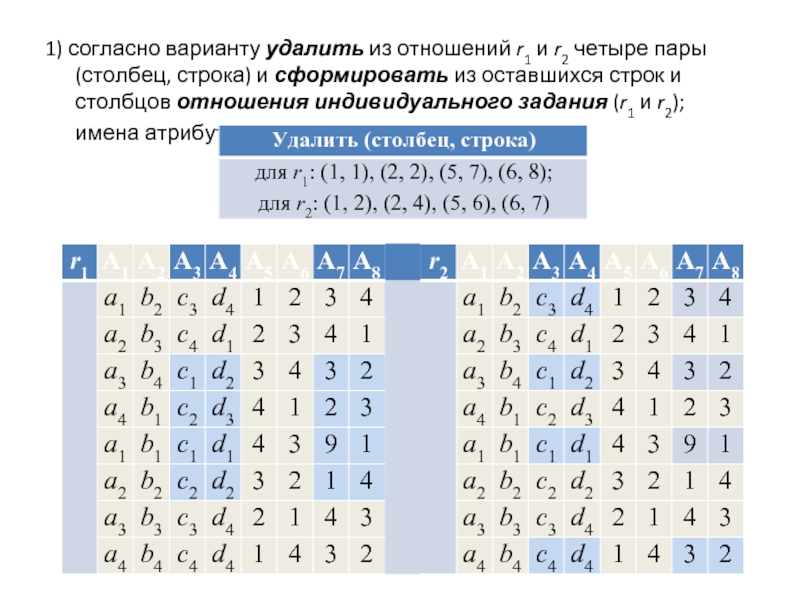
Слайд 391) согласно варианту удалить из отношений r1 и r2 четыре пары
(столбец, строка) и сформировать из оставшихся строк и столбцов отношения индивидуального задания (r1 и r2); имена атрибутов не изменять:
Слайд 412) выполнить операции (r1∪r2), (r1∩r2), (r1\r2) (r1⊗r2):
написать формулы реляционной алгебры и
реляционного исчисления,
нарисовать результирующие таблицы r’.
нарисовать результирующие таблицы r’.
Слайд 463) выполнить операции >< или >θ
вариантом из таблицы 4):
написать формулы реляционной алгебры и реляционного исчисления,
нарисовать результирующие таблицы:
написать формулы реляционной алгебры и реляционного исчисления,
нарисовать результирующие таблицы:
Таблица 4 Таблица 4
π(r1.A4, r2.A4, r2.A3)(δ((r1>θ
π(r1.A4, r2.A7, r2.A3)(δ((r1>