- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Логические законы и правила преобразования логических выражений презентация
Содержание
- 1. Логические законы и правила преобразования логических выражений
- 2. Основные законы формальной логики Закон тождества А
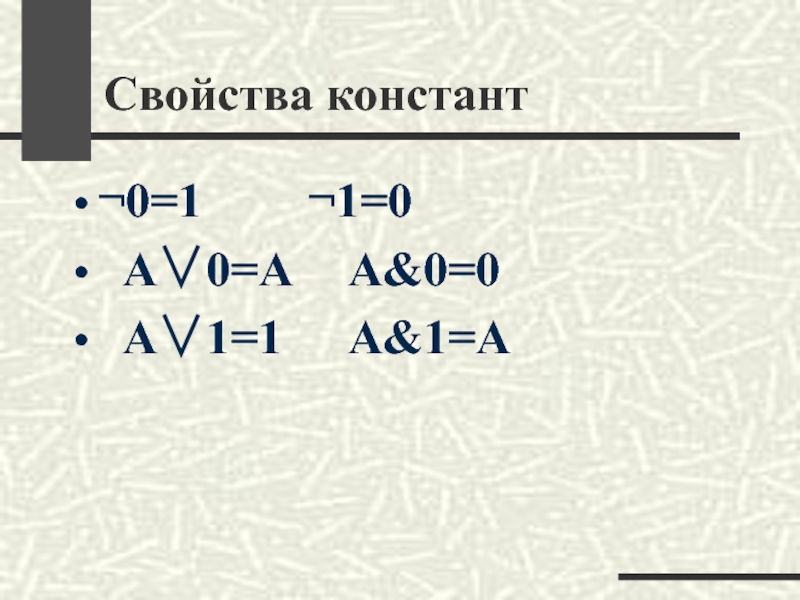
- 3. Свойства констант ¬0=1 ¬1=0 А∨0=А А&0=0 А∨1=1 А&1=А
- 4. Законы алгебры логики Идемпотентность А∨А=А А&А=А
- 5. Законы алгебры логики Дистрибутивность А ∨ (В
- 6. Огастес де МОРГАН
- 7. Правила замены операций Импликации А⇒ В =
- 8. Упрощение сложных высказываний - это замена их
- 9. Основные приемы замены X=X∧1 ⎤ X=X∨0 ⎦
- 10. Пример Упростить: А ∧В ∨ А ∧
Слайд 2Основные законы формальной логики
Закон тождества
А = А
Закон непротиворечия
А&¬A=0
Закон исключения третьего
А∨¬А=1
Закон двойного
¬¬А=А
В процессе рассуждения нельзя подменять одно понятие другим
Не могут быть одновременно истинными суждение и его отрицание
Высказывание может быть либо истинным либо ложным, третьего не дано
Если отрицать дважды некоторое суждение, то получается исходное суждение
Слайд 4Законы алгебры логики
Идемпотентность
А∨А=А А&А=А
Коммутативность
А ∨ В=В ∨ А А&В=В&А
Ассоциативность
А ∨ (В
А &(В & С)= (А & В) &С
Слайд 5Законы алгебры логики
Дистрибутивность
А ∨ (В & С)= (А ∨ В) &(A∨
А & (В ∨ С)= (А & В) ∨(A&С)
Поглощение
А ∨ (А & В)=А А & (А ∨ В)=А
Законы де Моргана
¬(А ∨В)= ¬ А&¬В ¬(А &В)= ¬ А ∨ ¬В
Слайд 6Огастес де МОРГАН
Морган Огастес (Августус) де (27.6.1806-18.3.
Слайд 7Правила замены операций
Импликации
А⇒ В = ¬А ∨ B А⇒ В =
Эквивалентности
А⇔В = (А&B) ∨ (¬A& ¬B)
А⇔В = (А ∨ ¬ B) ∨ (¬A ∨ B)
А⇔В = (А ⇒ B) & (B ⇒ A)
Слайд 8Упрощение сложных высказываний
- это замена их на равносильные на основе законов
Слайд 9Основные приемы замены
X=X∧1 ⎤
X=X∨0 ⎦
1=А ∨ ¬А
0=В ∧ ¬ В
Z=Z ∨Z
C=C ∧C ∧ C
Е= ¬ ¬Е
По свойствам констант
По закону исключения третьего
По закону непротиворечия
- По закону
идемпотентности
- По закону двойного отрицания
Слайд 10Пример
Упростить: А ∧В ∨ А ∧ ¬ В
По закону дистрибутивности
А ∧ В ∨ А ∧ ¬ В=
А ∧ 1=
А
А ∧(В ∨ ¬ В)=
Упростить: (А ∨ В )& (А ∨ ¬ В)
Упростить: ¬(¬ X ∨ ¬ Y )