- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Логические выражения и уравнения презентация
Содержание
- 1. Логические выражения и уравнения
- 2. Задача 1 Каким выражением
- 3. Задача 2 Каким выражением может
- 4. Задача 3 Логическая функция F задаётся выражением:
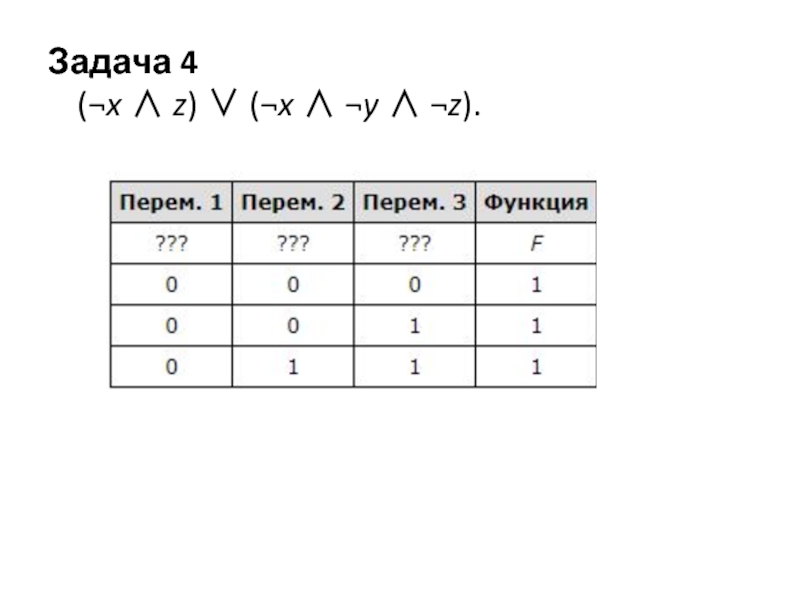
- 5. Задача 4 (¬x ∧ z) ∨ (¬x ∧ ¬y ∧ ¬z).
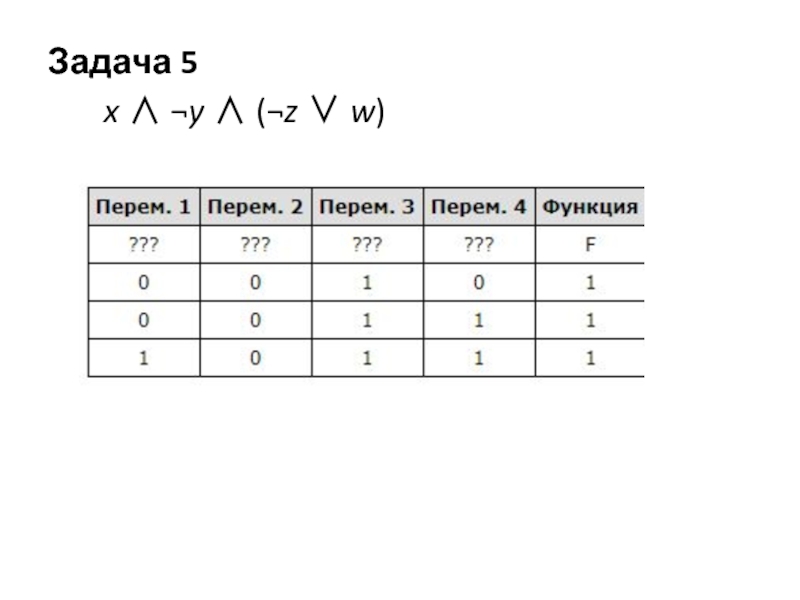
- 6. Задача 5 x ∧ ¬y ∧ (¬z ∨ w)
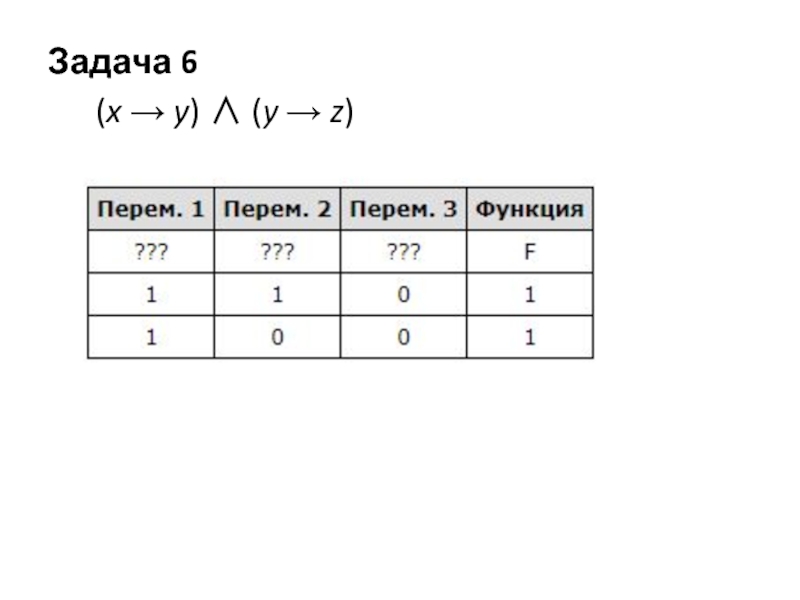
- 7. Задача 6 (x → y) ∧ (y → z)
- 8. Задача 7 Логическая функция F задаётся выражением
- 9. Задача 8 Какое выражение соответствует
- 10. Задача 9 Какое выражение соответствует
- 11. Задача 10 Элементами множества А
- 12. Задача 11 Элементами множеств
- 13. Задача 12 Для какого из
- 14. Задача 13 Обозначим через m & n поразрядную конъюнкцию
- 15. Задача 14 Обозначим через m
- 16. Задача 15 Для какого наибольшего
- 17. Задача 16 На числовой
- 18. Задача 17 На числовой прямой
- 19. Тест https://vk.com/smallu
Слайд 2
Задача 1
Каким выражением может быть F?
1) x1 ∧ x2
∧ x3 ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
2) x1 ∨ ¬x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ x6 ∨ ¬x7
3) ¬x1 ∧ x2 ∧ ¬x3 ∧ x4 ∧ x5 ∧ x6 ∧ x7
4) x1 ∨ x2 ∨ ¬ x3 ∨ x4 ∨ x5 ∨ ¬x6 ∨ x7
2) x1 ∨ ¬x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ x6 ∨ ¬x7
3) ¬x1 ∧ x2 ∧ ¬x3 ∧ x4 ∧ x5 ∧ x6 ∧ x7
4) x1 ∨ x2 ∨ ¬ x3 ∨ x4 ∨ x5 ∨ ¬x6 ∨ x7
Слайд 3
Задача 2
Каким выражением может быть F?
1) x1 ∧ (x2 →
x3) ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
2) x1 ∨ (¬x2 → x3) ∨ ¬x4 ∨ ¬x5 ∨ x6 ∨ ¬x7
3) ¬x1 ∧ (x2 → ¬x3) ∧ x4 ∧ x5 ∧ x6 ∧ x7
4) x1 ∨ (x2 → ¬ x3) ∨ x4 ∨ x5 ∨ ¬x6 ∨ x7
2) x1 ∨ (¬x2 → x3) ∨ ¬x4 ∨ ¬x5 ∨ x6 ∨ ¬x7
3) ¬x1 ∧ (x2 → ¬x3) ∧ x4 ∧ x5 ∧ x6 ∧ x7
4) x1 ∨ (x2 → ¬ x3) ∨ x4 ∨ x5 ∨ ¬x6 ∨ x7
Слайд 4
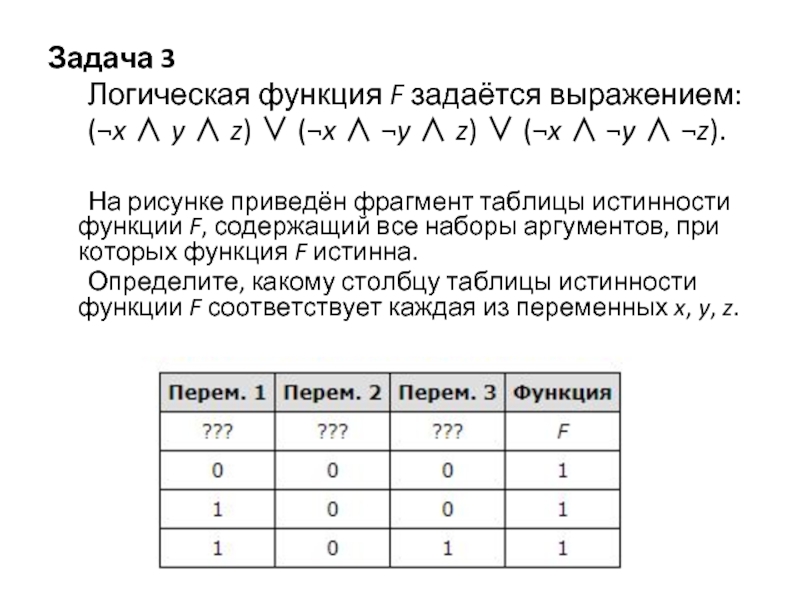
Задача 3
Логическая функция F задаётся выражением:
(¬x ∧ y ∧ z) ∨ (¬x ∧ ¬y ∧ z) ∨ (¬x ∧ ¬y ∧
¬z).
На рисунке приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F истинна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.
На рисунке приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F истинна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.
Слайд 8
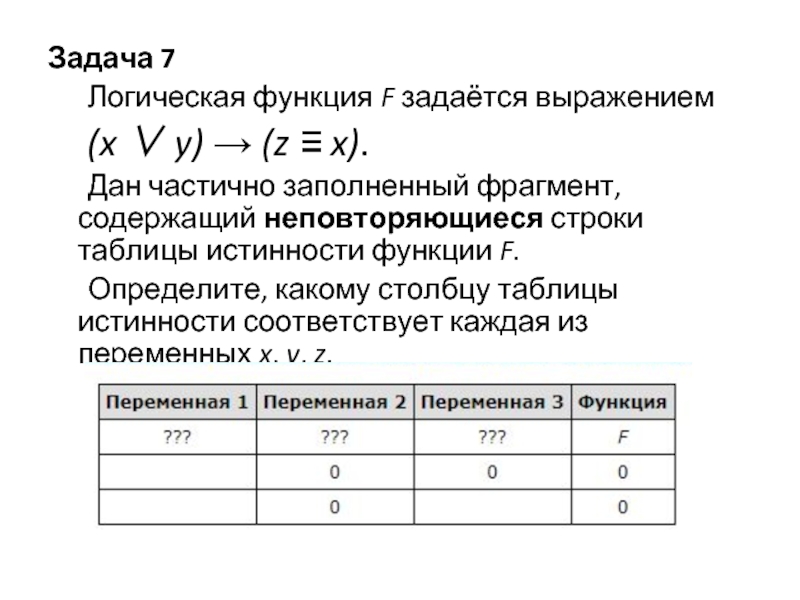
Задача 7
Логическая функция F задаётся выражением
(x ∨ y) → (z ≡ x).
Дан
частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.
Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z.
Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z.
Слайд 9
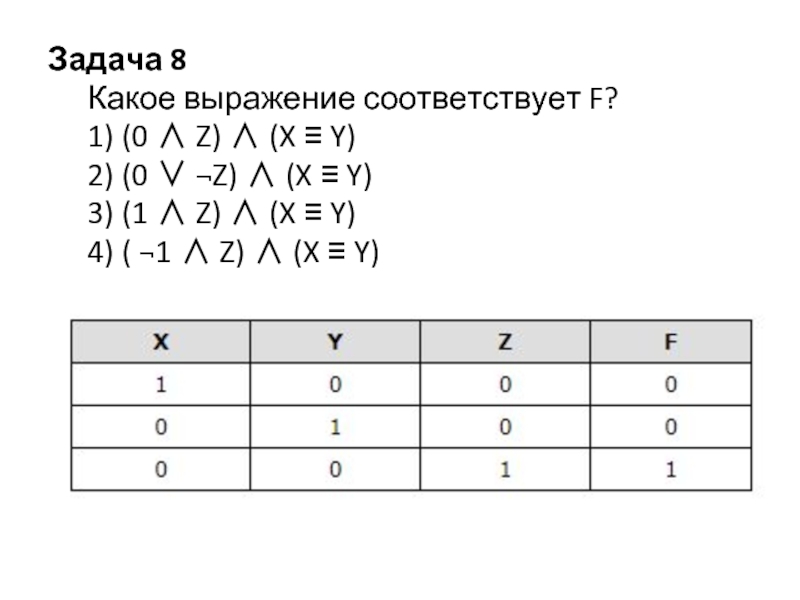
Задача 8
Какое выражение соответствует F?
1) (0 ∧ Z) ∧ (X
≡ Y)
2) (0 ∨ ¬Z) ∧ (X ≡ Y)
3) (1 ∧ Z) ∧ (X ≡ Y)
4) ( ¬1 ∧ Z) ∧ (X ≡ Y)
2) (0 ∨ ¬Z) ∧ (X ≡ Y)
3) (1 ∧ Z) ∧ (X ≡ Y)
4) ( ¬1 ∧ Z) ∧ (X ≡ Y)
Слайд 10
Задача 9
Какое выражение соответствует F?
1) (X ≡ Z) ∧ (¬X
→ Y)
2) (¬X ≡ Z) ∧ (¬X → Y)
3) (X ≡ ¬Z) ∧ (¬X → Y)
4) (X ≡ Z) ∧ (¬(Y → Z))
2) (¬X ≡ Z) ∧ (¬X → Y)
3) (X ≡ ¬Z) ∧ (¬X → Y)
4) (X ≡ Z) ∧ (¬(Y → Z))
Слайд 11
Задача 10
Элементами множества А являются натуральные числа. Известно, что выражение
(x
∈ {2, 4, 6, 8, 10, 12}) → (((x ∈ {3, 6, 9, 12, 15}) ∧ ¬(x ∈ A)) → ¬(x ∈ {2, 4, 6, 8, 10, 12}))
истинно (т. е. принимает значение 1) при любом значении переменной х. Определите наименьшее возможное значение суммы элементов множества A.
истинно (т. е. принимает значение 1) при любом значении переменной х. Определите наименьшее возможное значение суммы элементов множества A.
Слайд 12
Задача 11
Элементами множеств А, P, Q являются натуральные числа,
причём P = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20}, Q = {3, 6, 9, 12, 15, 18, 21, 24, 27, 30}.
Известно, что выражение
((x ∈ A) → (x ∈ P)) ∨ (¬(x ∈ Q) → ¬(x ∈ A))
истинно (т. е. принимает значение 1) при любом значении переменной х.
Определите наибольшее возможное количество элементов в множестве A.
Известно, что выражение
((x ∈ A) → (x ∈ P)) ∨ (¬(x ∈ Q) → ¬(x ∈ A))
истинно (т. е. принимает значение 1) при любом значении переменной х.
Определите наибольшее возможное количество элементов в множестве A.
Слайд 13
Задача 12
Для какого из приведённых чисел X истинно логическое условие:
¬((X кратно 5) → (X кратно 25))?
1) 37
2) 59
3) 65
4) 125
1) 37
2) 59
3) 65
4) 125
Слайд 14
Задача 13
Обозначим через m & n поразрядную конъюнкцию неотрицательных целых чисел m и n. Так, например, 14
& 5 = 11102 & 01012 = 01002 = 4. Для какого наименьшего неотрицательного целого числа А формула
x & 29 ≠ 0 → (x & 12 = 0 → x & А ≠ 0)
тождественно истинна (то есть принимает значение 1 при любом неотрицательном целом значении переменной х)?
x & 29 ≠ 0 → (x & 12 = 0 → x & А ≠ 0)
тождественно истинна (то есть принимает значение 1 при любом неотрицательном целом значении переменной х)?
Слайд 15
Задача 14
Обозначим через m & n поразрядную конъюнкцию неотрицательных целых
чисел m и n.
Например, 14 & 5 = 11102 & 01012 = 01002 = 4.
Для какого наименьшего неотрицательного целого числа А формула
x&77 ≠ 0 → (x&12 = 0 → x&А ≠ 0)
тождественно истинна (т. е. принимает значение 1 при любом неотрицательном целом значении переменной х)?
Например, 14 & 5 = 11102 & 01012 = 01002 = 4.
Для какого наименьшего неотрицательного целого числа А формула
x&77 ≠ 0 → (x&12 = 0 → x&А ≠ 0)
тождественно истинна (т. е. принимает значение 1 при любом неотрицательном целом значении переменной х)?
Слайд 16
Задача 15
Для какого наибольшего целого числа А формула
((x ≤ 9)
→(x ⋅ x ≤ A)) ⋀ ((y ⋅ y ≤ A) → (y ≤ 9))
тождественно истинна, то есть принимает значение 1 при любых целых неотрицательных x и y?
тождественно истинна, то есть принимает значение 1 при любых целых неотрицательных x и y?
Слайд 17
Задача 16
На числовой прямой даны два отрезка: P = [17, 46]
и Q = [22, 57]. Отрезок A таков, что приведённая ниже формула истинна при любом значении переменной х:
¬(x ∈ A) →(((x ∈ P) ⋀ (x ∈ Q)) → (x ∈ A))
Какова наименьшая возможная длина отрезка A?
¬(x ∈ A) →(((x ∈ P) ⋀ (x ∈ Q)) → (x ∈ A))
Какова наименьшая возможная длина отрезка A?
Слайд 18
Задача 17
На числовой прямой даны два отрезка: P = [8,
39] и Q = [23, 58].
Выберите из предложенных отрезков такой отрезок A, что логическое выражение
((x ∈ P) ∨ (x ∈ А)) → ((x ∈ Q) ∨ (x ∈ А))
тождественно истинно, то есть принимает значение 1 при любом значении переменной х.
1) [5, 30]
2) [15, 40]
3) [25, 50]
4) [35, 60]
Выберите из предложенных отрезков такой отрезок A, что логическое выражение
((x ∈ P) ∨ (x ∈ А)) → ((x ∈ Q) ∨ (x ∈ А))
тождественно истинно, то есть принимает значение 1 при любом значении переменной х.
1) [5, 30]
2) [15, 40]
3) [25, 50]
4) [35, 60]










![Задача 16 На числовой прямой даны два отрезка: P = [17, 46] и Q = [22, 57]. Отрезок A таков,](/img/tmb/1/58170/d30c9bfeb504b5ef5e99a5ec26e43ae2-800x.jpg)
![Задача 17 На числовой прямой даны два отрезка: P = [8, 39] и Q =](/img/tmb/1/58170/53324384f9c2e27ff3a7ea7445374836-800x.jpg)






