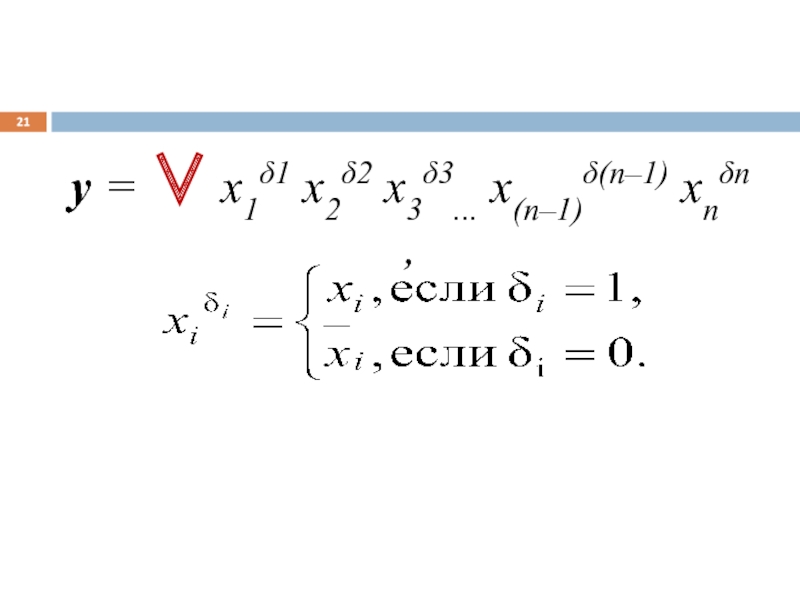- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Логические основы компьютерной техники. Булева алгебра презентация
Содержание
- 1. Логические основы компьютерной техники. Булева алгебра
- 2. Что такое Булева алгебра !? АЛГЕБРА –
- 3. В обычной алгебре (арифметической) над переменными
- 4. Операция дизъюнкции Аксиомы: 0+0 = 0;
- 5. Операция конъюнкции Аксиомы: 0•0 = 0;
- 6. Инверсия Аксиомы:
- 7. Полный список аксиом :
- 8. Формы представления булевых функций Булевы формулы могут
- 9. Формы представления булевых функций ЭЛЕМЕНТАРНАЯ КОНЪЮНКЦИЯ (ЭК)
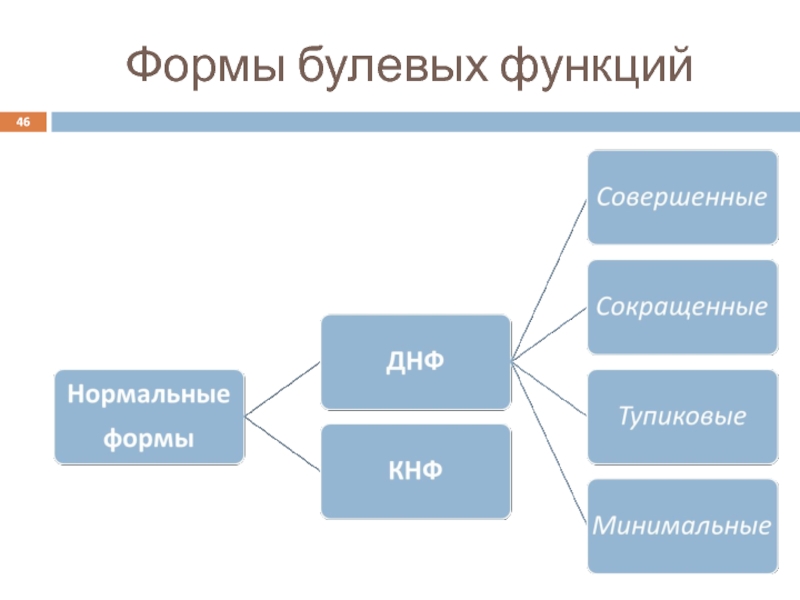
- 10. Нормальные формы ДИЗЪЮНКТИВНАЯ НОРМАЛЬНАЯ ФОРМА (ДНФ)
- 11. Нормальные формы КОНЪЮНКТИВНАЯ НОРМАЛЬНАЯ ФОРМА (КНФ)
- 12. Инвертирование сложных выражений Правило: Чтобы найти инверсию,
- 13. МИНТЕРМЫ Функции, которые принимают единичное значение только
- 14. МИНТЕРМЫ Минтермом n переменных называется такая их
- 15. Свойство: конъюнкция любых двух различных
- 16. МАКСТЕРМЫ Макстермом n переменных называется такая их
- 17. МАКСТЕРМЫ Макстермы обозначают большой буквой M с
- 18. Связь между индексами минтермов и макстермов :
- 19. Совершенные нормальные формы СОВЕРШЕННАЯ КОНЪЮНКТИВНАЯ НОРМАЛЬНАЯ ФОРМА (СКНФ) СОВЕРШЕННАЯ ДИЗЪЮНКТИВНАЯ НОРМАЛЬНАЯ ФОРМА (СДНФ)
- 20. СОВЕРШЕННАЯ ДИЗЪЮНКТИВНАЯ НОРМАЛЬНАЯ ФОРМА – это ДНФ,
- 21. y = ∨ х1δ1 х2δ2 х3δ3... х(n–1)δ(n–1) хnδn ,
- 22. Всякая булева функция для заданного числа
- 23. СОВЕРШЕННАЯ КОНЪЮНКТИВНАЯ НОРМАЛЬНАЯ ФОРМА – это КНФ,
- 24. y = ∧ ( х1δ1 +
- 25. Карта Вейча её модификацию называют диаграммой Карно
- 26. Карта Вейча для 3-х аргументов
- 27. Карта Вейча для 4-х аргументов
- 28. Карта Вейча для 5-х аргументов
- 29. Нанесение функций на карту Вейча Пусть есть
- 30. Минимальная ДНФ (МДНФ) МДНФ булевой функции называется
- 31. Импликанта булевой функции Функция g(x1, …,
- 32. Импликанта булевой функции, которая представлена элементарной
- 33. Пример импликант: Пусть дана функция:
- 34. Импликанты ф-ции f = AB + BC
- 35. Методы минимизации функций алгебры логики минимизация
- 36. минимизация методом Квайна Основу метода составляет теорема
- 38. Выражение, полученное методом Квайна, называется сокращённой
- 39. Для всякой булевой функции существует единственная сокращённая ДНФ
- 40. Найти методом Квайна минимальное выражение для функции y
- 41. 1–й этап
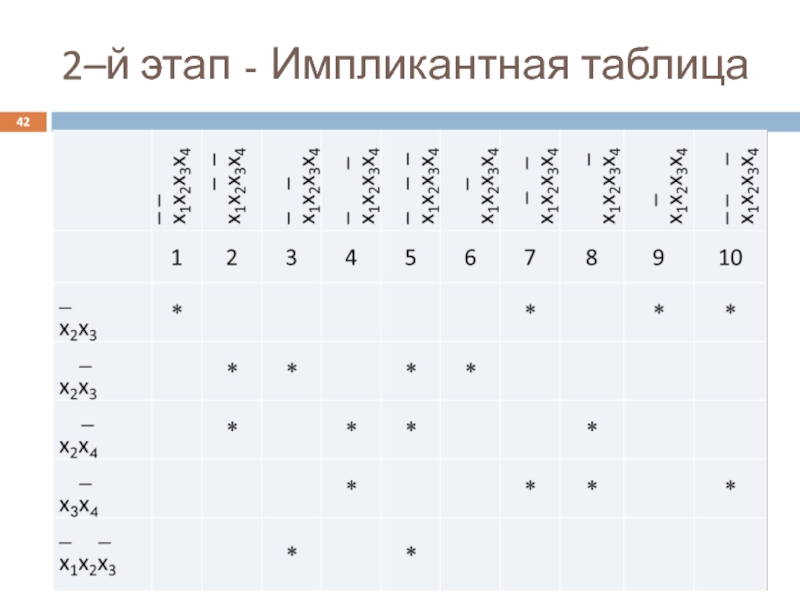
- 42. 2–й этап - Импликантная таблица
- 43. Получение минимальной ДНФ Функция «покрыта» полностью
- 44. Минимальная ДНФ из 3-х импликант
- 45. Граф-схема булевой функции
- 46. Формы булевых функций
- 47. Литература по теме: Лысиков Б. Г. Арифметические
Что такое Булева алгебра !? АЛГЕБРА – … ??? БУЛЕВА АЛГЕБРА – … ??? раздел математики, посвященный изучению операций над элементами множеств, которые могут так или
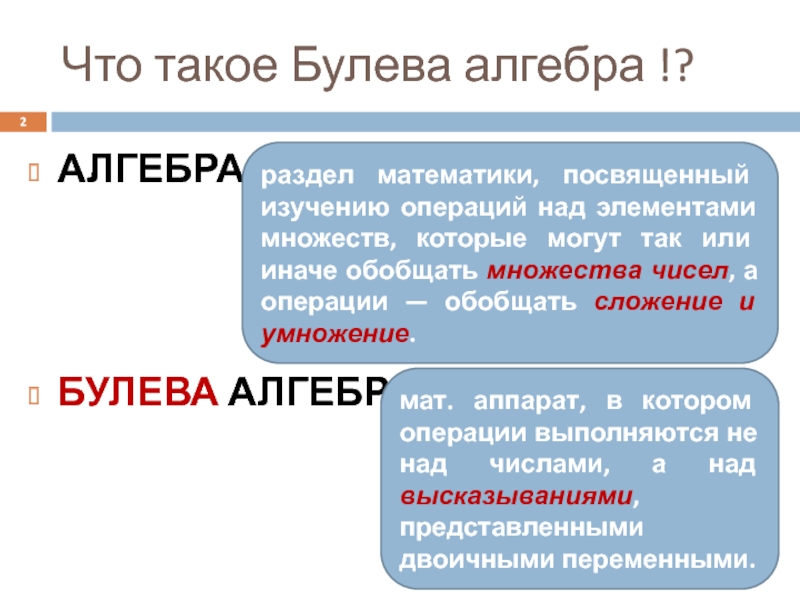
Слайд 2Что такое Булева алгебра !?
АЛГЕБРА – … ???
БУЛЕВА АЛГЕБРА –
… ???
раздел математики, посвященный изучению операций над элементами множеств, которые могут так или иначе обобщать множества чисел, а операции — обобщать сложение и умножение.
мат. аппарат, в котором операции выполняются не над числами, а над высказываниями, представленными двоичными переменными.
Слайд 3
В обычной алгебре (арифметической) над переменными (чаще это числа) выполняются операции
сложения / вычитания, умножения / деления и т. д.
В булевой алгебре основными являются только три операции:
дизъюнкция, конъюнкция, инверсия.
В булевой алгебре основными являются только три операции:
дизъюнкция, конъюнкция, инверсия.
Слайд 8Формы представления булевых функций
Булевы формулы могут быть записаны либо в виде
дизъюнкции, либо в виде конъюнкции каких-либо выражений.
В первом случае говорят о ДИЗЪЮНКТИВНОЙ ФОРМЕ,
во втором— о КОНЪЮНКТИВНОЙ ФОРМЕ.
В первом случае говорят о ДИЗЪЮНКТИВНОЙ ФОРМЕ,
во втором— о КОНЪЮНКТИВНОЙ ФОРМЕ.
Слайд 9Формы представления булевых функций
ЭЛЕМЕНТАРНАЯ КОНЪЮНКЦИЯ (ЭК) –
логическое произведение любого конечного
числа различных между собой булевых переменных, взятых со знаком инверсии или без него.
ЭЛЕМЕНТАРНАЯ ДИЗЪЮНКЦИЯ (ЭД) –
логическая сумма любого конечного числа различных между собой булевых переменных, взятых со знаком инверсии или без него.
ЭЛЕМЕНТАРНАЯ ДИЗЪЮНКЦИЯ (ЭД) –
логическая сумма любого конечного числа различных между собой булевых переменных, взятых со знаком инверсии или без него.
Слайд 10Нормальные формы
ДИЗЪЮНКТИВНАЯ НОРМАЛЬНАЯ ФОРМА (ДНФ)
– булева формула, которая записана
в виде дизъюнкции выражений, каждое из которых представляет собой либо отдельный аргумент (с инверсией или без инверсии), либо конъюнкцию некоторых аргументов.
– дизъюнкция конечного числа ЭК.
– дизъюнкция конечного числа ЭК.
Слайд 11Нормальные формы
КОНЪЮНКТИВНАЯ НОРМАЛЬНАЯ ФОРМА (КНФ)
– булева формула, которая записана
в виде конъюнкции выражений, каждое из которых представляет собой либо отдельный аргумент (с инверсией или без инверсии), либо дизъюнкцию некоторых аргументов.
– конъюнкция конечного числа ЭД.
– конъюнкция конечного числа ЭД.
Слайд 12Инвертирование сложных выражений
Правило:
Чтобы найти инверсию, необходимо знаки умножения заменить знаками сложения,
а знаки сложения — знаками умножения и поставить инверсии над каждой переменной.
(независимо от того, есть над переменными знаки отрицания или нет)
(независимо от того, есть над переменными знаки отрицания или нет)
Слайд 13МИНТЕРМЫ
Функции, которые принимают единичное значение только на одном наборе называются
минимальными
термами,
или — МИНТЕРМАМИ
(иногда конституентами единицы).
Слайд 14МИНТЕРМЫ
Минтермом n переменных называется такая их конъюнкция, в которую каждая переменная
входит только один раз в прямой или инверсной форме.
Обозначаются минтермы буквой m с десятичным индексом, являющимся номером минтерма.
Обозначаются минтермы буквой m с десятичным индексом, являющимся номером минтерма.
mi
m0 = 000…0
Слайд 15
Свойство:
конъюнкция любых двух различных минтермов, зависящих от одних и тех
же аргументов, тождественно равна нулю.
Слайд 16МАКСТЕРМЫ
Макстермом n переменных называется такая их дизъюнкция, в которую каждая переменная
входит только один раз в прямой или инверсной форме.
Макстерм (конституента нуля) — это булева функция, которая принимает единичное значение на всех наборах, за исключением одного.
Макстерм (конституента нуля) — это булева функция, которая принимает единичное значение на всех наборах, за исключением одного.
Слайд 17МАКСТЕРМЫ
Макстермы обозначают большой буквой M с десятичными индексами (по аналогии с
обозначением минтермов).
СВОЙСТВО:
дизъюнкция любых двух различных макстермов, зависящих от одних и тех же аргументов, равна единице.
СВОЙСТВО:
дизъюнкция любых двух различных макстермов, зависящих от одних и тех же аргументов, равна единице.
Mi
Слайд 19Совершенные нормальные формы
СОВЕРШЕННАЯ КОНЪЮНКТИВНАЯ НОРМАЛЬНАЯ ФОРМА (СКНФ)
СОВЕРШЕННАЯ ДИЗЪЮНКТИВНАЯ НОРМАЛЬНАЯ ФОРМА
(СДНФ)
Слайд 20СОВЕРШЕННАЯ ДИЗЪЮНКТИВНАЯ НОРМАЛЬНАЯ ФОРМА – это
ДНФ, в которой все конъюнкции имеют
ранг n
дизъюнкция минтермов n аргументов
дизъюнкцию простых конъюнкций
дизъюнкция минтермов n аргументов
дизъюнкцию простых конъюнкций
простые конъюнкции содержат все переменные в своей прямой или инверсной форме
Слайд 22
Всякая булева функция для заданного числа аргументов представима в виде суммы
минтермов единственным образом.
Поэтому СДНФ называют стандартной формой, или канонической.
Поэтому СДНФ называют стандартной формой, или канонической.
Слайд 23СОВЕРШЕННАЯ КОНЪЮНКТИВНАЯ НОРМАЛЬНАЯ ФОРМА – это
КНФ, в которой все дизъюнкции имеют
ранг n
конъюнкция макстермов n аргументов
конъюнкция простых дизъюнкций.
конъюнкция макстермов n аргументов
конъюнкция простых дизъюнкций.
простая дизъюнкция – дизъюнкция переменных или их отрицаний
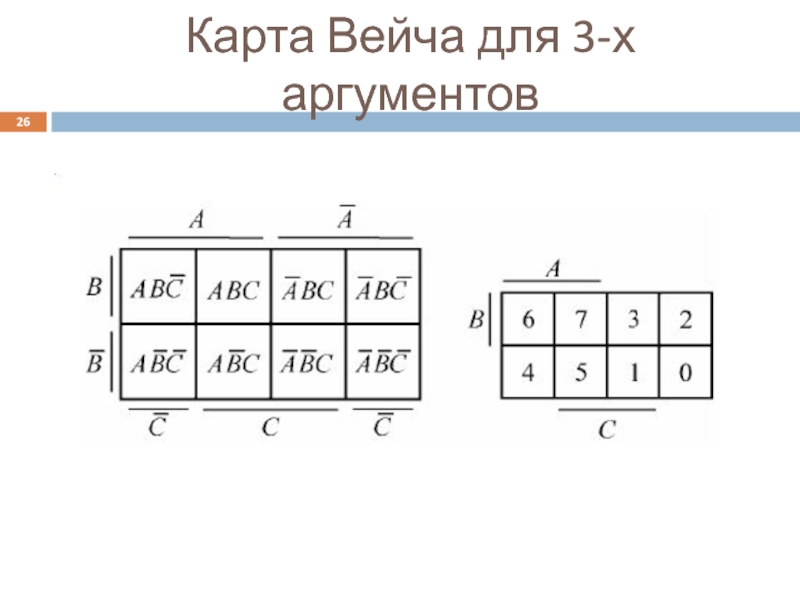
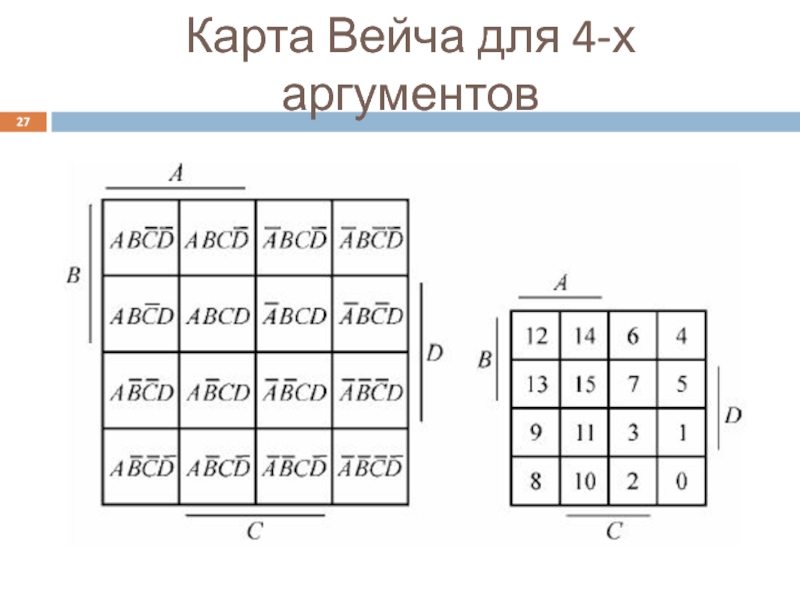
Слайд 25Карта Вейча
её модификацию называют диаграммой Карно
На рис.1 приведены минтермы функции от
двух переменных А и В.
На рис.2 указаны десятичные номера минтермов.
На рис.2 указаны десятичные номера минтермов.
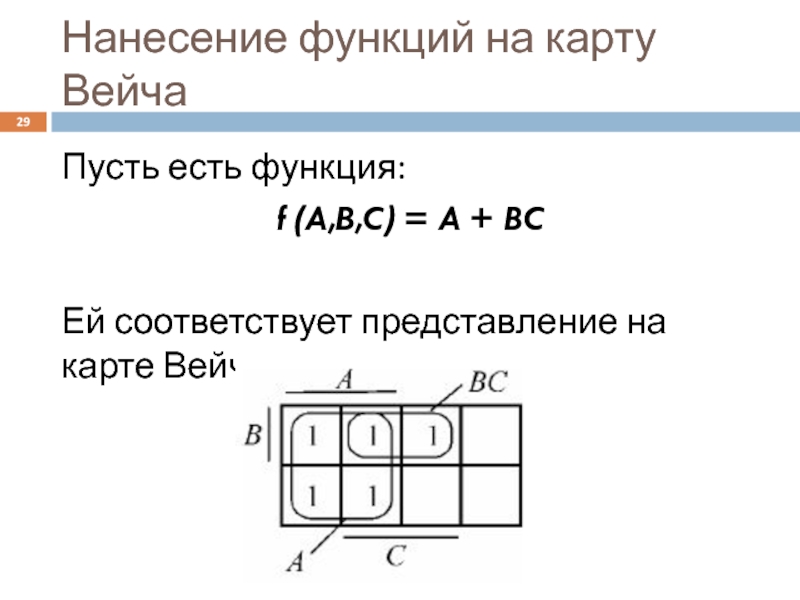
Слайд 29Нанесение функций на карту Вейча
Пусть есть функция:
f (A,B,C) = A +
BC
Ей соответствует представление на карте Вейча:
Ей соответствует представление на карте Вейча:
Слайд 30Минимальная ДНФ (МДНФ)
МДНФ булевой функции называется ДНФ, которая содержит наименьшее число
букв в записи (по отношению ко всем другим ДНФ этой функции).
Слайд 31Импликанта булевой функции
Функция g(x1, …, xn) называется импликантой функции f(x1,
…, xn), если для любого набора аргументов, на котором g=1, справедливо что f=1.
Слайд 32
Импликанта булевой функции, которая представлена элементарной конъюнкцией, называется простой, если никакая
ее часть больше не является импликантой этой функции.
Т.Е. простая импликанта – это такая, к которой нельзя применить операцию склеивания.
Т.Е. простая импликанта – это такая, к которой нельзя применить операцию склеивания.
Слайд 33Пример импликант:
Пусть дана функция:
f = AB + BC.
Представим её
в СДНФ:
f = (3,6,7) .
Эта функция содержит три минтерма. Из них можно образовать семь различных функций, каждая из которых является импликантой функции f.
f = (3,6,7) .
Эта функция содержит три минтерма. Из них можно образовать семь различных функций, каждая из которых является импликантой функции f.
Слайд 35Методы минимизации
функций алгебры логики
минимизация методом Квайна;
минимизация с использованием карт Карно;
минимизация
не полностью определенных (частичных) функций;
минимизация КНФ;
минимизация методом кубического задания функций алгебры логики;
минимизация методом Квайна–Мак–Класски;
минимизация с использованием алгоритма извлечения (Рота);
минимизация ФАЛ методом преобразования логических выражений.
минимизация КНФ;
минимизация методом кубического задания функций алгебры логики;
минимизация методом Квайна–Мак–Класски;
минимизация с использованием алгоритма извлечения (Рота);
минимизация ФАЛ методом преобразования логических выражений.
Слайд 36минимизация методом Квайна
Основу метода составляет теорема склеивания, которая применяется к каждой
паре минтермов заданной функции.
Например:
f (A,B,C,D) = (0, 1, 3, 6, 7, 8, 12, 13, 14, 15)
Например:
f (A,B,C,D) = (0, 1, 3, 6, 7, 8, 12, 13, 14, 15)
Слайд 38
Выражение, полученное методом Квайна, называется сокращённой дизъюнктивной нормальной формой заданной функции,
а каждая его конъюнкция называется простой импликантой.
Слайд 47Литература по теме:
Лысиков Б. Г. Арифметические и логические основы цифровых автоматов
// Минск: Высшая школа, 1980. – 268 с.
Савельев А. Я. Прикладная теория цифровых автоматов: учебник для вузов по специальности ЭВМ // М.: Высшая школа, 1987. – 462 с.
Шевелев Ю. П. Дискретная математика. Ч. 1: Теория множеств. Булева алгебра Автоматизированная технология обучения «Символ»): Учебное пособие // Томск. гос. ун-т систем управления и радиоэлектроники, 2003. — 118 с.
Савельев А. Я. Прикладная теория цифровых автоматов: учебник для вузов по специальности ЭВМ // М.: Высшая школа, 1987. – 462 с.
Шевелев Ю. П. Дискретная математика. Ч. 1: Теория множеств. Булева алгебра Автоматизированная технология обучения «Символ»): Учебное пособие // Томск. гос. ун-т систем управления и радиоэлектроники, 2003. — 118 с.
