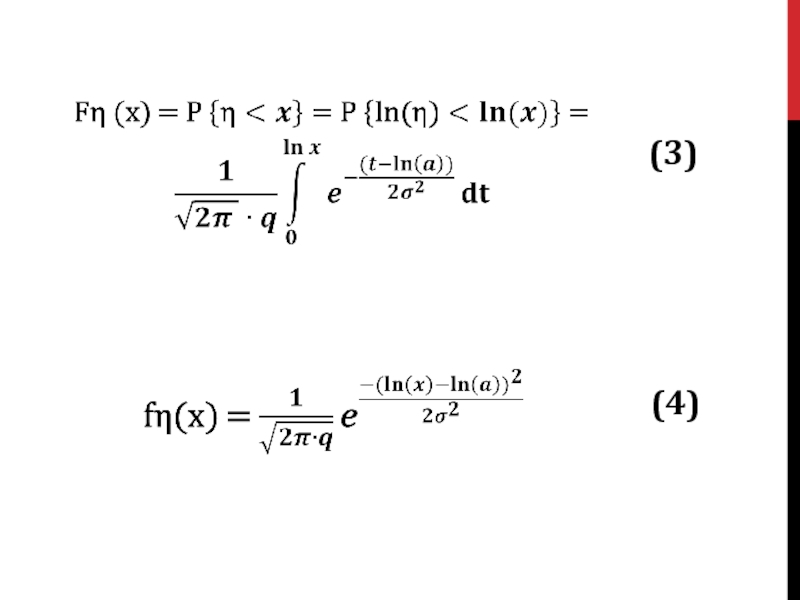- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Логарифмически-нормальное (логонормальное) распределение презентация
Содержание
- 1. Логарифмически-нормальное (логонормальное) распределение
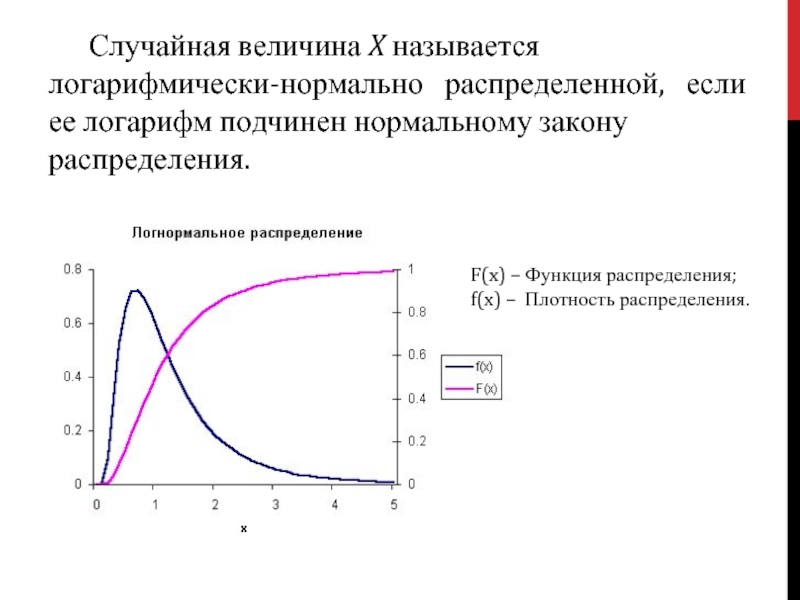
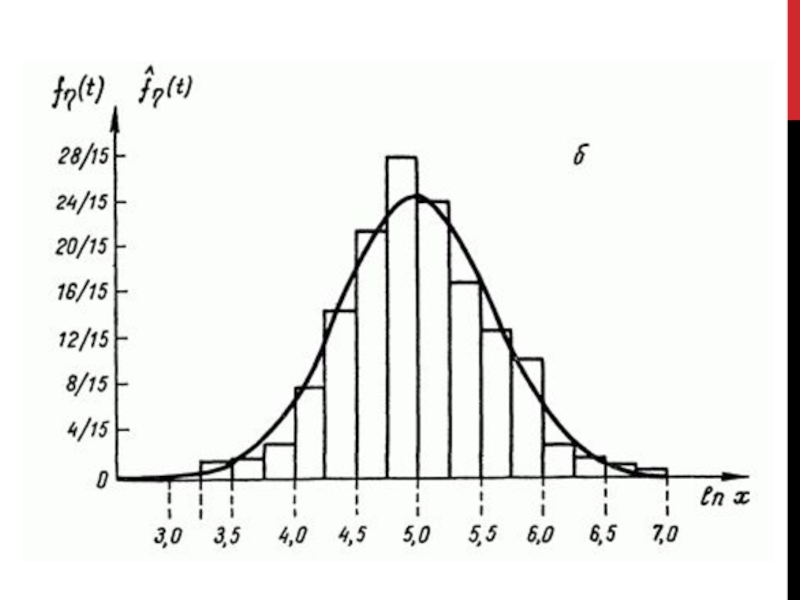
- 2. Случайная величина X называется логарифмически-нормально распределенной, если ее логарифм подчинен нормальному закону распределения. F(x) – Функция распределения; f(x) – Плотность распределения.
- 3. f(x) – Плотность распределения F(x) – Функция распределения , при μ=0
- 4. η1 = η0 + ξ1 * η0
- 5. (3) (4)
- 10. Основные числовые характеристики
- 11. Список использованной литературы Колмогоров А. Н., О
Случайная величина X называется логарифмически-нормально распределенной, если ее логарифм подчинен нормальному закону распределения. F(x) – Функция распределения; f(x) – Плотность распределения.
Слайд 1Логарифмически-нормальное (логонормальное)
распределение
Выполнили с-ты гр. 4АМ61:
Стрыгин К.В.
Караваев В.Е.
Слайд 2 Случайная величина X называется логарифмически-нормально распределенной, если ее логарифм подчинен нормальному закону распределения.
F(x) – Функция распределения;
f(x) – Плотность
распределения.
Слайд 4η1 = η0 + ξ1 * η0 ;
η2 = η1 +
ξ2 * η1 ;
--------------------
ηN = ηN-1 + ξN * ηN-1
--------------------
ηN = ηN-1 + ξN * ηN-1
= ξ1 + ξ2 + … + ξN (1)
η0 = a - неслучайная компонента исследуемого фактора η;
ξ1, ξ2, … , ξN - численное выражение эффектов воздействия упомянутых случайных факторов
Слайд 11Список использованной литературы
Колмогоров А. Н., О логарифмически-нормальном законе распределения размеров частиц
при дроблении, «Докл. АН СССР», 1941, т. 31, в. 2, с. 99—101;
Айвазян С. А. и др. Прикладная статистика: Основы моделирования и первичная обработка данных. Справочное изд. / С. А. Айвазян, И. С. Енюков, Л. Д. Мешалкин. — М.: Финансы и статистика, 1983. — 471 с.
Современные риск системы [Электронный ресурс] / А. Новоселов. – Электрон. текстовые дан. – Красноярск: 2014. – Режим доступа: http://risktheory.novosyolov.com/distr_lognormal.htm
Айвазян С. А. и др. Прикладная статистика: Основы моделирования и первичная обработка данных. Справочное изд. / С. А. Айвазян, И. С. Енюков, Л. Д. Мешалкин. — М.: Финансы и статистика, 1983. — 471 с.
Современные риск системы [Электронный ресурс] / А. Новоселов. – Электрон. текстовые дан. – Красноярск: 2014. – Режим доступа: http://risktheory.novosyolov.com/distr_lognormal.htm
