Оценка качества уравнения множественной регрессии.
4. Частные критерии.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Линейная множественная регрессия презентация
Содержание
- 1. Линейная множественная регрессия
- 2. 1. Линейная модель множественной регрессии
- 3. Множественный регрессионный анализ
- 4. Вторая
- 5. Будем далее
- 6. Для построения
- 7. Тогда наблюдаемые значения переменных должны удовлетворять уравнению
- 8. Оценкой уравнения (1) по выборке является выборочное
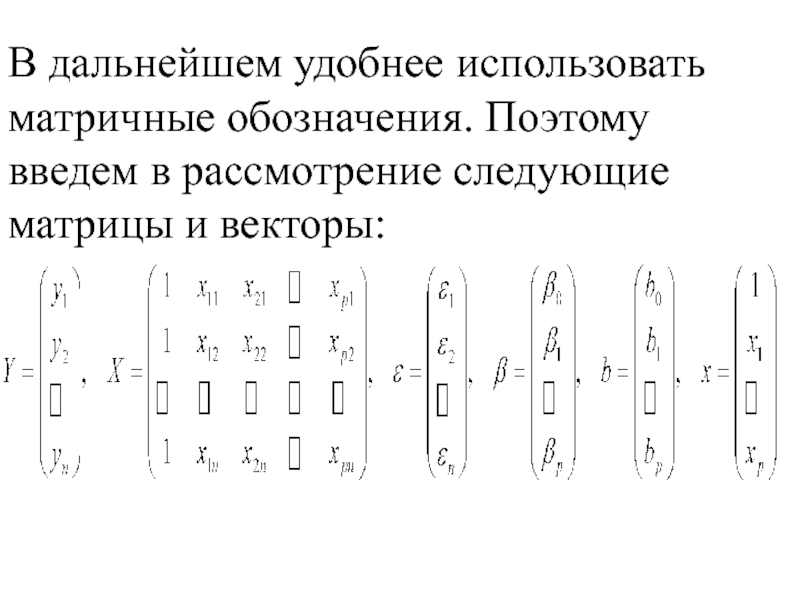
- 9. В дальнейшем удобнее использовать матричные обозначения. Поэтому введем в рассмотрение следующие матрицы и векторы:
- 10. Тогда уравнение регрессии (1) в матричной форме
- 11. Чтобы получить оценку вектора методом
- 12. При выполнении указанных предпосылок (1° - 6°)
- 13. 2. Ранжирование факторов Если бы все
- 14. Однако в общем случае переменные имеют различные
- 15. где
- 16. Имея значения , можно
- 17. Чем больше модуль
- 18. От уравнения вида
- 19. Для оценки влияния отдельных факторов на переменную
- 20. Коэффициент частной корреляции характеризует тесноту линейной связи
- 21. Например, частными
- 22. Отсюда
- 23. При
- 24. 3. Оценка качества уравнения множественной регрессии По
- 25. Величину называют коэффициентом
- 26. который представляет собой обобщение парного коэффициента корреляции
- 27. Коэффициент является неубывающей функцией числа объясняющих
- 28. Доказано, что
- 29. Проверка статистического качества модели выполняется путем проверки
- 30. Для проверки данной гипотезы используется статистика:
- 31. Найденное по формуле (7) значение сравнивается с
- 32. Как
- 33. Здесь
- 34. Если
- 35. если
- 36. Так же
- 37. Зафиксируем значения прогнозных объясняющих
- 38. Тогда
- 39. 4. Частные критерии
- 40. Мерой оценки
- 41. Если в модели
- 42. Фактические значения частных критериев , найденных по
- 43. В противном
- 44. Пусть по
- 45. Если
- 46. Если при этом
1. Линейная модель множественной регрессии Если любая парная регрессия статистически незначима, то следует искать зависимость объясняемой переменной либо от другого фактора, либо от нескольких факторов.
Слайд 1Лекция 3
Линейная множественная регрессия
1. Линейная модель множественной регрессии.
2. Ранжирование факторов.
3.
Слайд 21. Линейная модель множественной регрессии
Если любая парная
регрессия статистически незначима, то следует искать зависимость объясняемой переменной либо от другого фактора, либо от нескольких факторов.
В последнем случае задача решается с помощью множественного регрессионного анализа.
В последнем случае задача решается с помощью множественного регрессионного анализа.
Слайд 3 Множественный регрессионный анализ является обобщением парного, однако
здесь появляются новые проблемы, из которых следует выделить две.
Первая из них связана со спецификацией модели, которая теперь включает в себя отбор факторов и выбор вида уравнения.
При отборе факторов необходимо ответить на вопрос: какие факторы существенно влияют на , а какие – несущественно, и последние не следует включить в регрессию.
Первая из них связана со спецификацией модели, которая теперь включает в себя отбор факторов и выбор вида уравнения.
При отборе факторов необходимо ответить на вопрос: какие факторы существенно влияют на , а какие – несущественно, и последние не следует включить в регрессию.
Слайд 4 Вторая проблема связана с исследованием
влияния конкретной независимой переменной на признак ,
т.е. разграничения её воздействия от влияния других независимых переменных.
т.е. разграничения её воздействия от влияния других независимых переменных.
Слайд 5 Будем далее считать, что факторы
отобраны правильно, а в качестве уравнения связи с признаком выбрана наиболее употребляемая и простая линейная модель множественной регрессии
Слайд 6 Для построения модели требуются исходные статистические
данные в виде следующей многомерной выборки ( ):
Слайд 7Тогда наблюдаемые значения переменных должны удовлетворять уравнению
, (1)
где значение признака в м наблюдении, значение го фактора в м наблюдении, случайная составляющая в м наблюдении.
Слайд 9В дальнейшем удобнее использовать матричные обозначения. Поэтому введем в рассмотрение следующие
матрицы и векторы:
Слайд 10Тогда уравнение регрессии (1) в матричной форме запишется
а выборочное уравнение (2)
примет вид
.
Отсюда нетрудно получить
где
.
Слайд 11 Чтобы получить оценку вектора методом наименьших квадратов, дополнительно к
предпосылкам МНК для парной регрессии 1° -5° здесь требуется выполнение ещё одного условия:
6°. Столбцы матрицы должны быть линейно-независимы, т.е. ранг матрицы должен быть равен (числу столбцов).
Слайд 12При выполнении указанных предпосылок (1° - 6°) искомый вектор определяется из
системы нормальных уравнений в матри-чной форме:
Решением этого уравнения является МНК - оценка
(4)
Решением этого уравнения является МНК - оценка
(4)
Слайд 132. Ранжирование факторов
Если бы все объясняющие переменные
в уравнении
(2) измерялись в одних и
тех же единицах, например, в кг,
то непосредственно сопоставляя абсолютные
значения коэффициентов регрессии
тех же единицах, например, в кг,
то непосредственно сопоставляя абсолютные
значения коэффициентов регрессии
можно было ранжировать факторы
по силе их воздействия на признак
Чем больше
тем сильнее фактор
влияет на
.
Слайд 14Однако в общем случае переменные имеют различные единицы измерения и такое
ранжирование невозможно (ошибочно). В этом случае прибегают к нормированию коэффициентов регрессии – вычислению стандартизованных коэффициентов регрессии по следующей формуле
(5)
(5)
Слайд 15где средние
квадратические отклонения переменных соответственно.
Коэффициент показывает, на сколько в среднем изменится переменная , если соответствующий фактор увеличится на одно при неизменном среднем уровне других факторов модели.
Слайд 16Имея значения , можно построить уравнение множественной регрессии
в стандартизованном масштабе
(6)
где ,
стандартизованные переменные, для которых средние значения равны нулю
( 0), а средние квадратические отклонения равны единице ( ).
(6)
где ,
стандартизованные переменные, для которых средние значения равны нулю
( 0), а средние квадратические отклонения равны единице ( ).
Слайд 17 Чем больше модуль ,
тем сильнее влияние фактора на признак , т.е. по значениям можно выполнить непосредственное ранжирование факторов по силе их воздействия на .
Слайд 18 От уравнения вида (6) можно перейти к
уравнению регрессии в натуральном масштабе (2), используя формулы:
Слайд 19Для оценки влияния отдельных факторов на переменную также можно использовать средние
коэффициенты эластичности
Ранжирование факторов по силе воздействия на можно выполнить также с помощью частных коэффициентов корреляции.
Ранжирование факторов по силе воздействия на можно выполнить также с помощью частных коэффициентов корреляции.
Слайд 20Коэффициент частной корреляции характеризует тесноту линейной связи между признаком
и фактором при устранении (элиминировании) влияния других факторов, включенных в модель.
Различают коэффициенты частной корреляции 1, 2, …,( ) – го порядков, если рассматривается регрессия с числом факторов, равным .
Различают коэффициенты частной корреляции 1, 2, …,( ) – го порядков, если рассматривается регрессия с числом факторов, равным .
Слайд 21 Например, частными коэффициентами корреляции являются:
коэффициент первого порядка, учитывающий связь и фактора при неизменном действии фактора ;
коэффициент 2-го порядка, учитывающий связь и фактора при неизменном действии факторов ;
коэффициент 2-го порядка, учитывающий связь и фактора при неизменном действии факторов ;
Слайд 22 Отсюда коэффициент парной
корреляции
можно рассматривать как частный коэффициент 0-го порядка.
Коэффициенты частной корреляции более высоких порядков определяются через коэффициенты низких порядков. Для случая, когда вычисляют два частных коэффициента первого порядка:
Коэффициенты частной корреляции более высоких порядков определяются через коэффициенты низких порядков. Для случая, когда вычисляют два частных коэффициента первого порядка:
Слайд 23 При этом существует связь между
частными коэффициентами корреляции и стандартизованными коэффициентами регрессии:
Слайд 243. Оценка качества уравнения множественной регрессии
По аналогии с парной регрессией можно
определить долю результата , объясненной вариацией включенных в модель факторов в его общей дисперсии:
Слайд 25Величину называют коэффициентом множественной детерминации. Он служит
измерителем качества подбора уравнения. Его значения изменяются в пределах от 0 до 1, и чем ближе к единице, тем больше уравнение регрессии объясняет поведение .
Кроме коэффициента используют другой показатель качества – коэффициент множественной корреляции
Кроме коэффициента используют другой показатель качества – коэффициент множественной корреляции
Слайд 26который представляет собой обобщение парного коэффициента корреляции и
характеризует совместное (совокупное) влияние всех факторов на результат . В отличие от коэффициент множественной корреляции принимает значения от 0 до 1 и не может быть использован для интерпретации направления связи.
Слайд 27Коэффициент является неубывающей функцией числа объясняющих переменных. Если добавить в
модель фактор, который совсем не влияет на , то обязательно автоматически увеличится. Этот недостаток можно устранить, если определять показатель не через суммы квадратов, а через дисперсии на одну степень свободы. В результате получаем скорректированный (нормированный) коэффициент множе-ственной детерминации:
Слайд 28
Доказано, что увеличивается при добавлении нового
фактора в модель тогда и только тогда, когда модуль статистики параметра по этой переменной больше единицы. Значение может даже уменьшится при добавлении нового фактора.
Слайд 29Проверка статистического качества модели выполняется путем проверки совокупной значимости её коэффициентов,
т.е. проверки гипотезы:
На практике вместо указанной гипотезы проверяют тесно связанную с ней гипотезу о статистической значимости коэффициента детерминации :
Слайд 30
Для проверки данной гипотезы используется статистика:
(7)
которая имеет распределение Фишера.
Слайд 31Найденное по формуле (7) значение сравнивается с ,
которое находится по таблицам по заданному уровню значимости и числу степеней свободы и . Если , то гипотеза отклоняется и это равносильно статистической значимости уравнения в целом.
Слайд 32 Как и в случае парной
регрессии выполняется статистическая значимость отдельных коэффициентов уравнения на основе статистик:
(8)
где стандартная ошибка параметра , вычисляемая по формуле:
(8)
где стандартная ошибка параметра , вычисляемая по формуле:
Слайд 33Здесь
диагональный элемент обратной матрицы , стоящий на пересечении й строки и го столбца; несмещенная оценка дисперсии возмущения , определяемая по формуле:
Слайд 34Если , где
находится из таблиц по значению и числу степеней свободы то коэффициент считается статистически значимым.
Приведенную строгую проверку значимости коэффициентов можно заменить простым сравнительным анализом ("грубое" правило):
Приведенную строгую проверку значимости коэффициентов можно заменить простым сравнительным анализом ("грубое" правило):
Слайд 35 если ,
то статистически незначим;
если , то относительно значим, и для уточнения следует воспользоваться строгой методикой;
если , то статистически значим;
если , то считается сильно значимым и вероятность ошибки вывода не превосходит 0,001.
если , то относительно значим, и для уточнения следует воспользоваться строгой методикой;
если , то статистически значим;
если , то считается сильно значимым и вероятность ошибки вывода не превосходит 0,001.
Слайд 36 Так же как и в парной
регрессии для статистически значимых коэффициентов модели можно построить интервальные оценки:
где прежнее значение критической точки распределения.
Доверительный интервал можно построить и для индивидуальных прогнозных значений зависимой переменной .
где прежнее значение критической точки распределения.
Доверительный интервал можно построить и для индивидуальных прогнозных значений зависимой переменной .
Слайд 37 Зафиксируем значения прогнозных объясняющих переменных
и по вектору-столбцу
найдем прогнозное значение зависимой переменной :
Слайд 38 Тогда доверительный интервал для индивидуального
прогнозного значения в точке примет вид
где стандартная ошибка вычисляется по формуле:
где стандартная ошибка вычисляется по формуле:
Слайд 394. Частные критерии
Не каждый фактор, дополнительно включаемый
в модель, может существенно увеличить долю объясненной вариации зависимой переменной. Ввиду корреляции между факторами значимость одного и того же фактора может быть различной в зависимости от последовательности включения его в модель.
Слайд 40 Мерой оценки значимости улучшения качества модели,
в которой были включены факторы , после включения в неё дополнительно фактора , служит частный критерий:
где коэффициент множественной детерминации для модели без фактора , тот же коэффициент с включенным в модель фактором .
где коэффициент множественной детерминации для модели без фактора , тот же коэффициент с включенным в модель фактором .
Слайд 42Фактические значения частных критериев , найденных по формуле (9), сравнивается
с
, определяемое по таблицам распределения Фишера по заданному уровню значимости и числам степеней свободы и .
Если, например, , то включение фактора в модель, после того как в уравнение уже включен фактор , статистически оправдано и параметр при факторе статистически значим.
Если, например, , то включение фактора в модель, после того как в уравнение уже включен фактор , статистически оправдано и параметр при факторе статистически значим.
Слайд 43 В противном случае дополнительное включение в
модель фактора не увеличивает существенно долю объясненной вариации и, следовательно, включение фактора в модель неце-леобразно.
По аналогичной схеме проверяется целесообразность включения (или исключения) не одного, а группы факторов.
По аналогичной схеме проверяется целесообразность включения (или исключения) не одного, а группы факторов.
Слайд 44 Пусть по наблюдениям построено уравнение
регрессии с факторами и коэффициент множественной детерминации равен . Дополнительно в модель включают ещё факторов и коэффициент детерминации при этом составит величину ( ). Тогда проверяется гипотеза с помощью статистики
Слайд 45Если
, то гипотеза отклоняется и одновременное включение факторов в модель обоснованно.
Если из модели одновременно исключаются факторов, то используют статистику
где коэффициенты детерминации с и факторами соответственно.
Если из модели одновременно исключаются факторов, то используют статистику
где коэффициенты детерминации с и факторами соответственно.
Слайд 46Если при этом
, то гипотеза отклоняется и одновременное исключение факторов из модели некорректно, так как существенно превышает .
