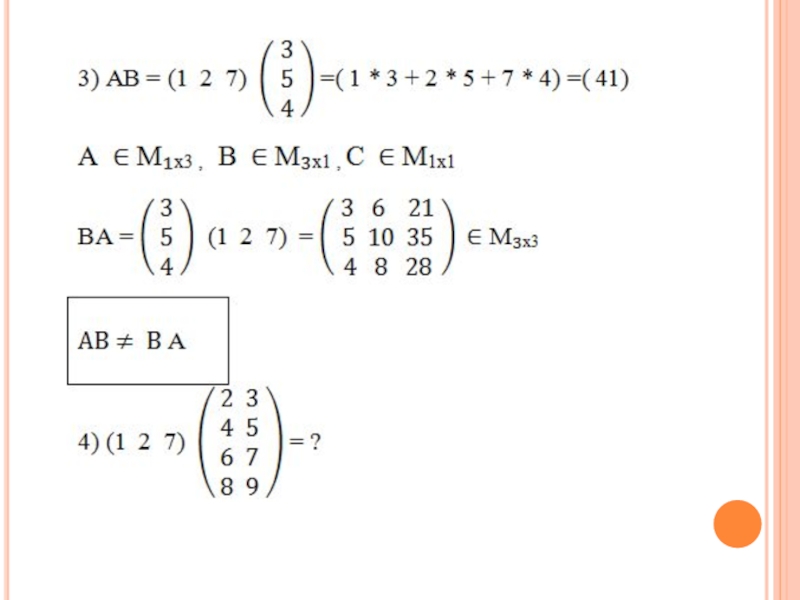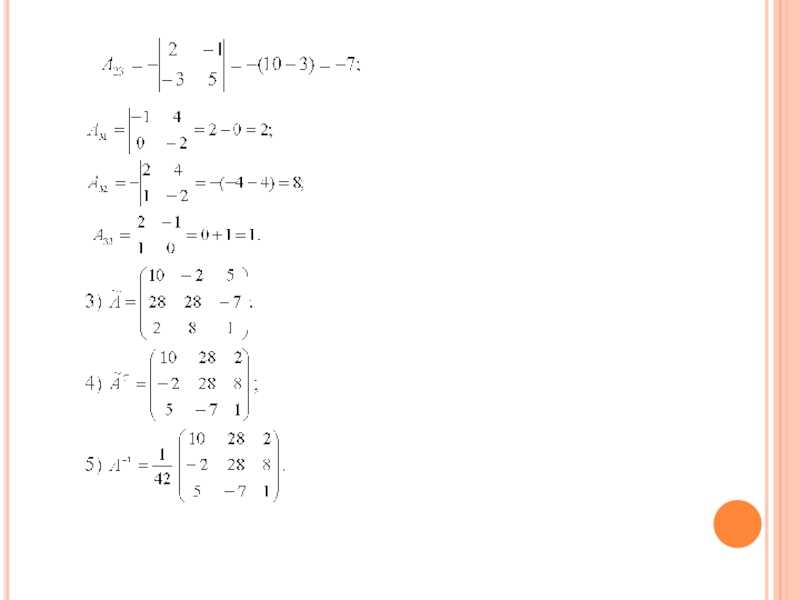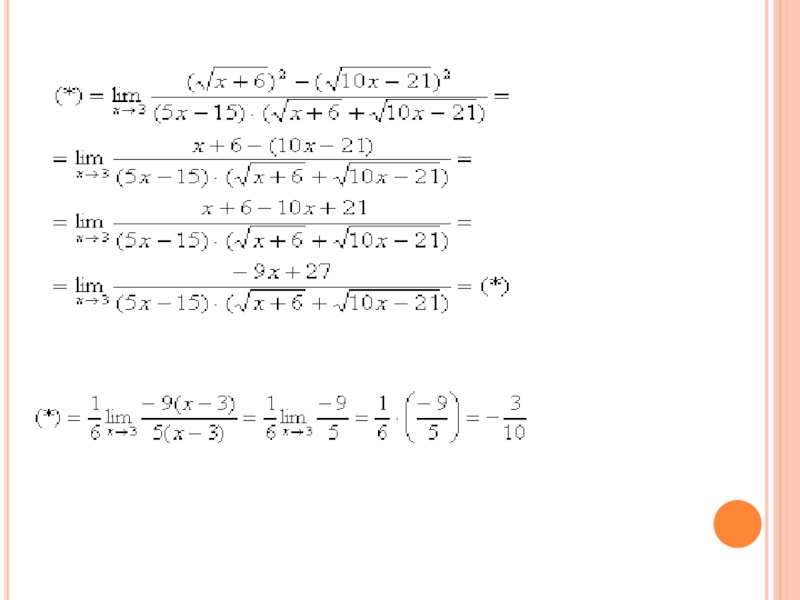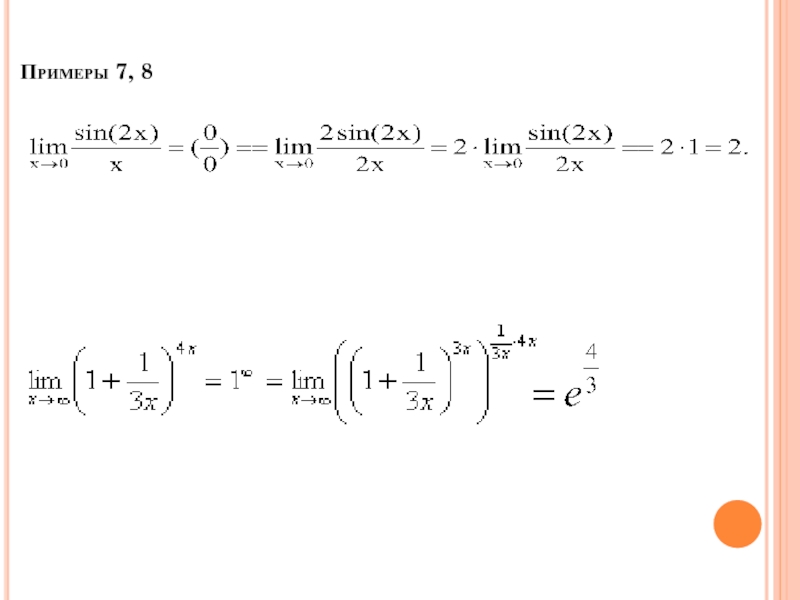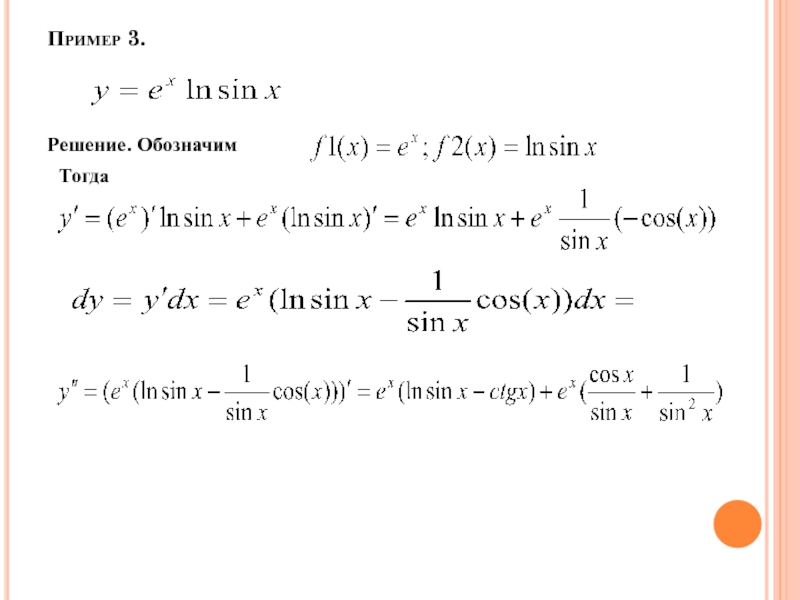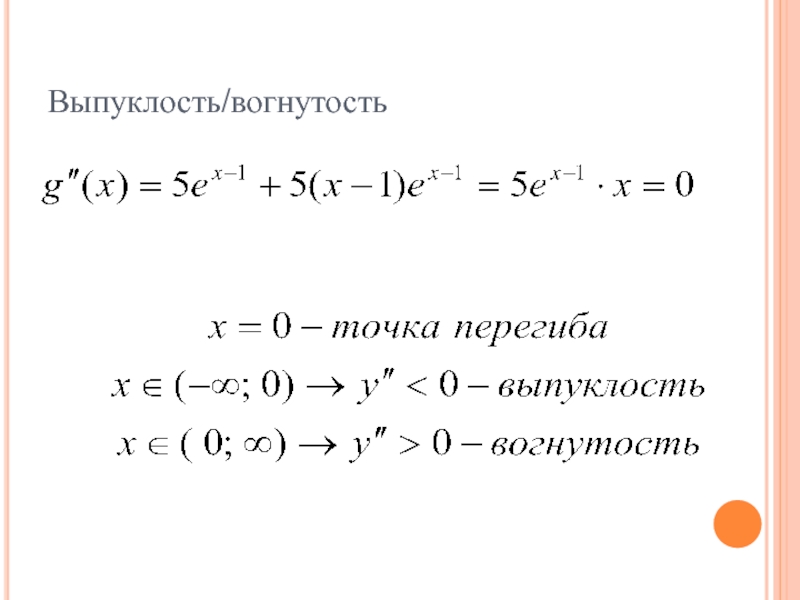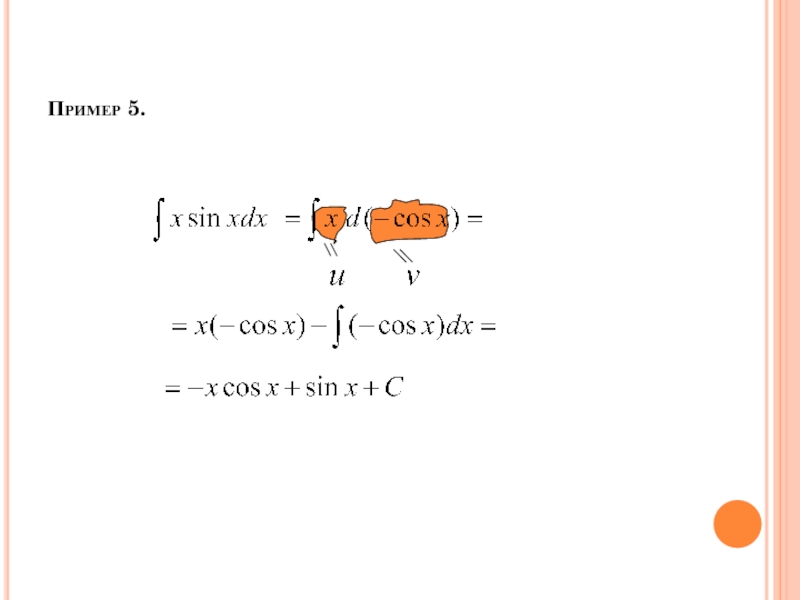- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Линейная алгебра. Выполнение операций над матрицами презентация
Содержание
- 1. Линейная алгебра. Выполнение операций над матрицами
- 2. Примеры. 1. Выполните операции над матрицами 1)
- 6. 2. Вычислить определитель матрицы
- 9. 3. Вычислить матрицу, обратную данной
- 11. Сделаем проверку
- 12. 4. Найти ранг матрицы
- 14. 5. Решить систему уравнений
- 16. 6. Найти косинус угла между векторами
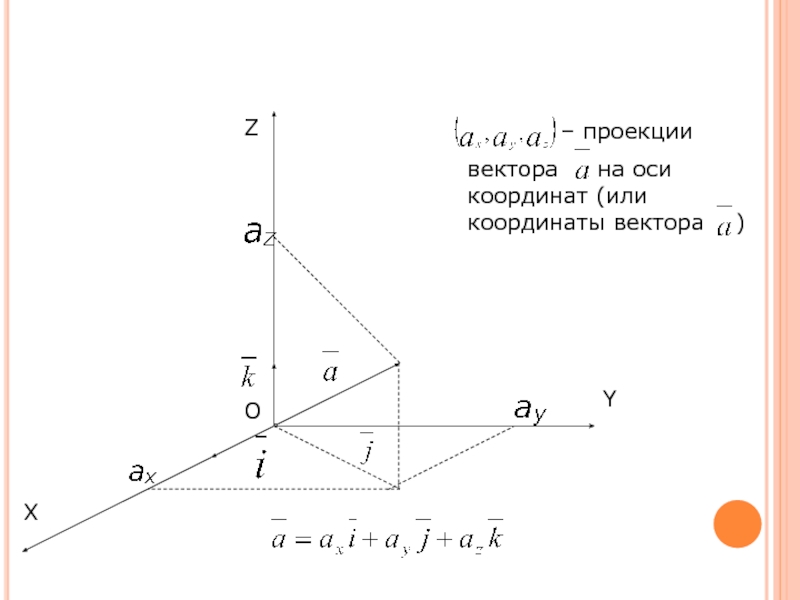
- 18. O X Y Z
- 19. Пример. Найти векторное произведение векторов Решение.
- 20. 7. Уравнение прямой
- 22. Пример 2. Составить уравнение прямой, проходящей через
- 23. 8. Кривые второго порядка
- 24. Окружность
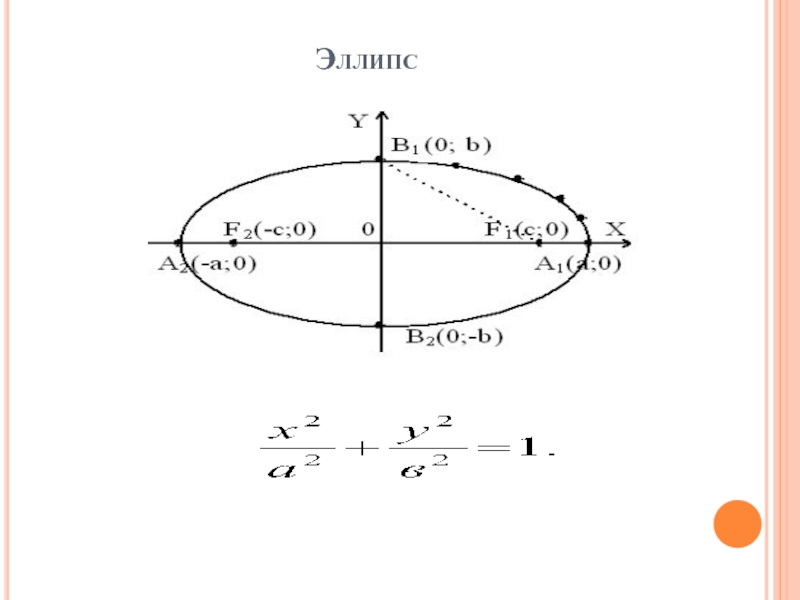
- 25. Эллипс
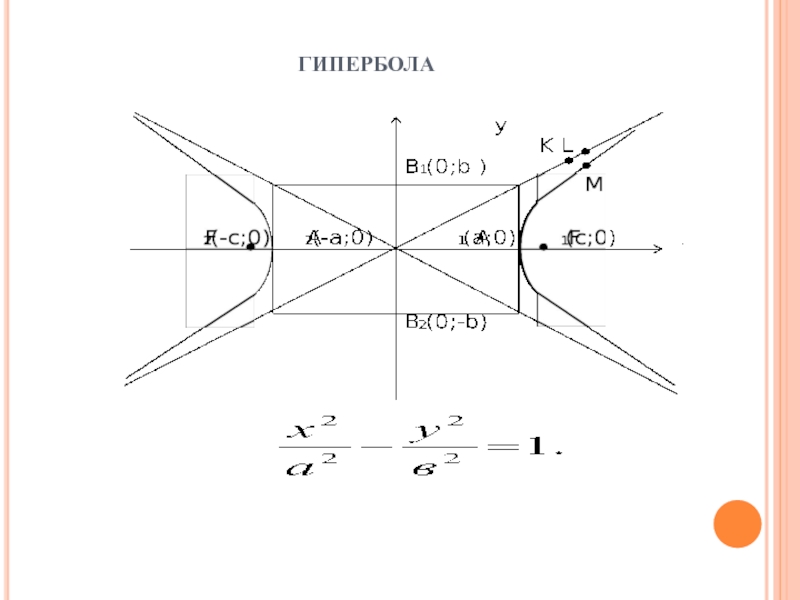
- 26. гипербола
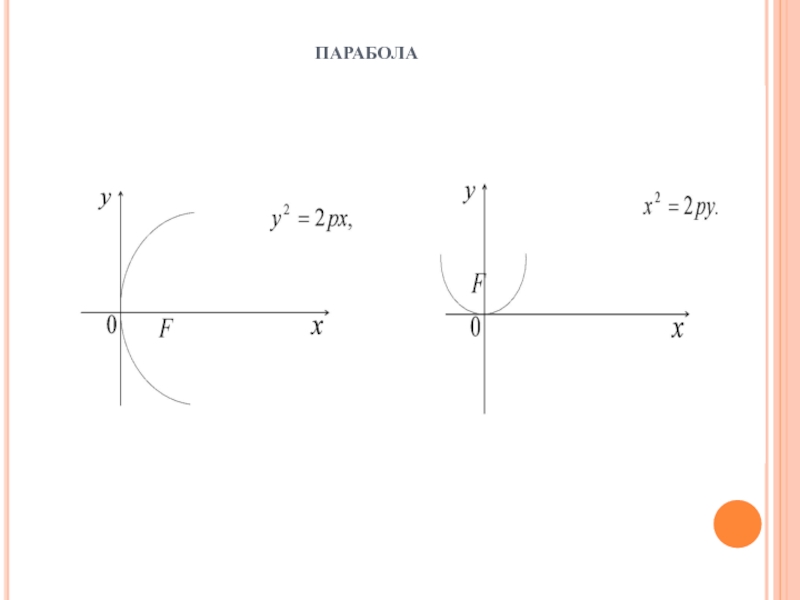
- 27. парабола
- 30. Пример 3.
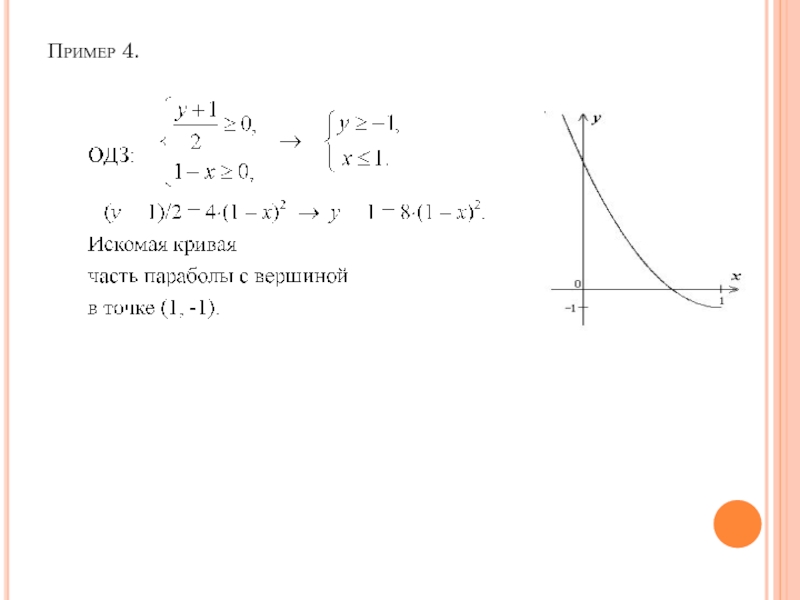
- 31. Пример 4.
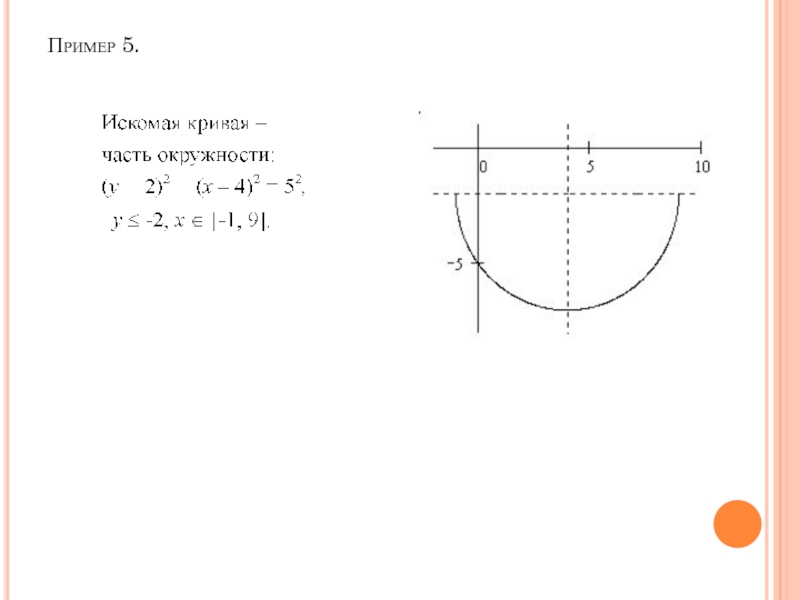
- 32. Пример 5.
- 33. Пример 6. Определить тип кривой и схематически
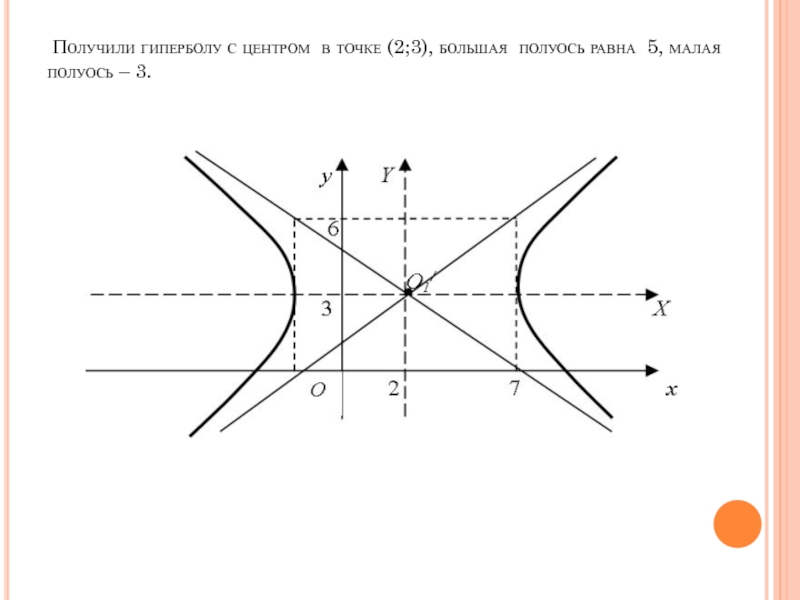
- 34. Получили гиперболу с центром в точке
- 35. МАТЕМАТИЧЕСКИЙ АНАЛИЗ (практическое занятие)
- 36. пределы Пример 1. Вычислить предел
- 37. Пример 2. Вычислить предел Решение.
- 38. Пример 3.
- 39. пример
- 40. Пример 5. Вычислить предел Сначала попробуем
- 41. Пример 6. Найти предел Сначала пробуем подставить
- 43. Примеры 7, 8
- 44. Пример 9. Вычислить предел Решение.
- 45. Производная функции Пример 1. Вычислить первую и
- 46. Пример 2 Решение. Обозначим: f1(x)=3x; f2(x)=
- 47. Пример 3. Решение. Обозначим
- 48. Пример 4. Вычислить производную функции
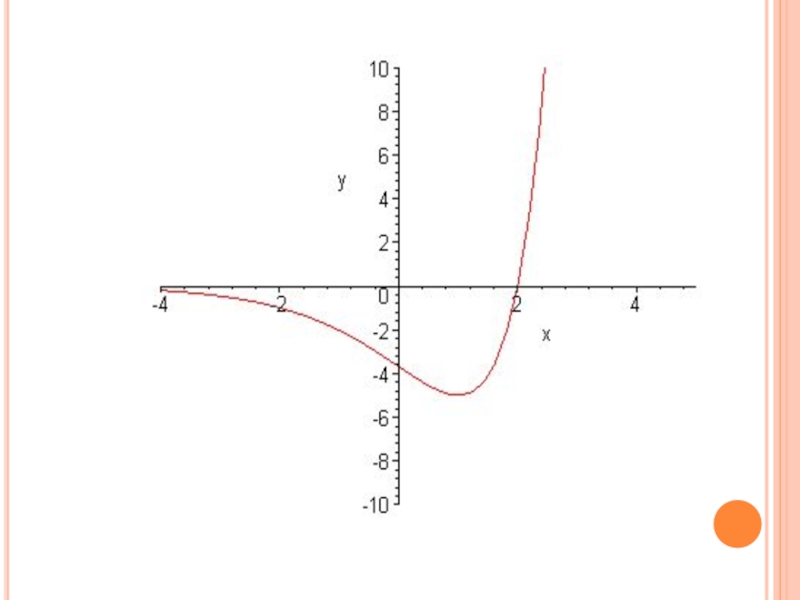
- 50. Пример 5. Исследовать функцию g(x) и построить
- 51. Экстремумы, возрастание, убывание
- 52. Выпуклость/вогнутость
- 54. Интегральное исчисление
- 56. Пример 3. Вычислить интеграл Найти
- 57. Пример 4. Вычислить интеграл
- 58. Пример 5.
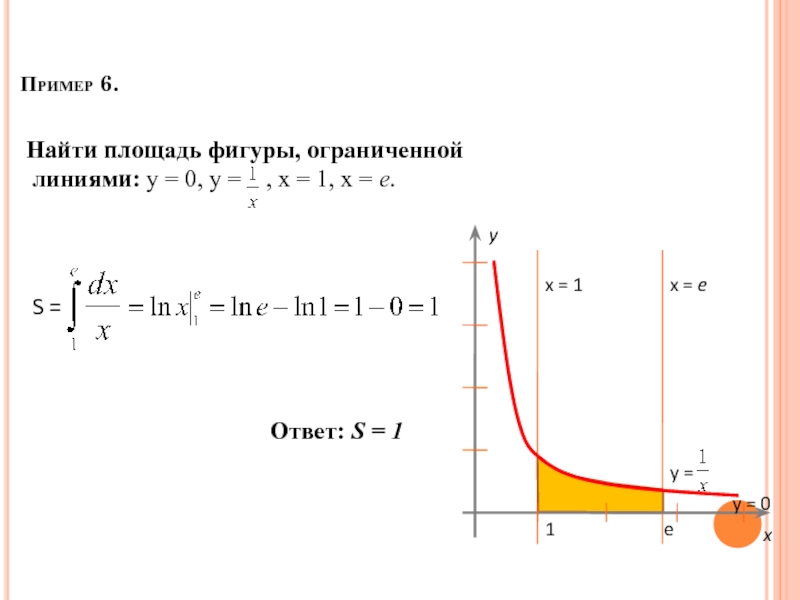
- 59. Пример 6. S = Ответ: S = 1
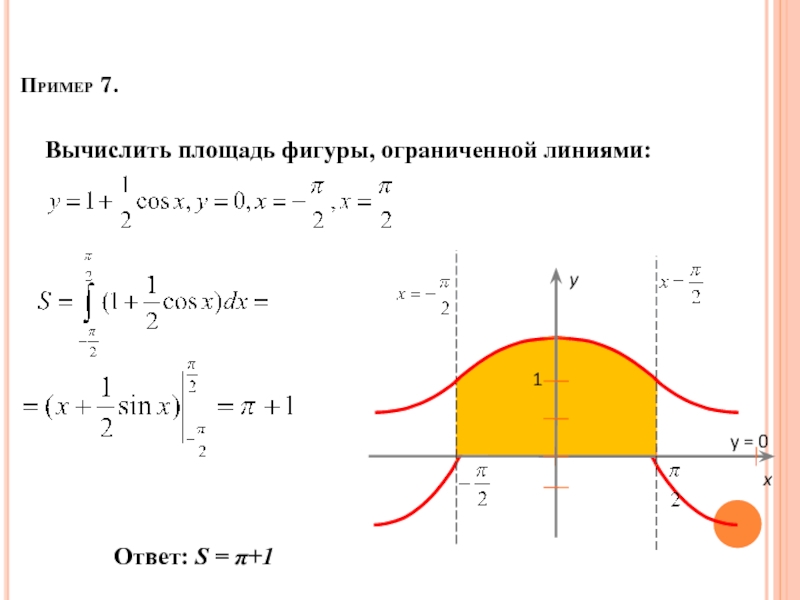
- 60. Пример 7. Ответ: S = π+1
- 61. Пример 8. Вычислить площадь фигуры, ограниченной
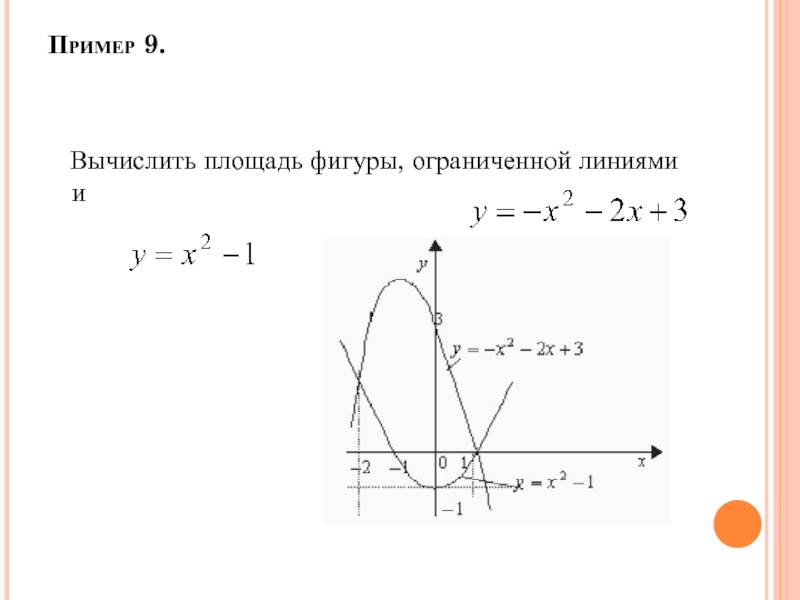
- 62. Пример 9. Вычислить площадь
Слайд 22Пример 2. Составить уравнение прямой, проходящей через точки М1(2; 3) и
Решение. Воспользуемся формулой:
Разрешим полученное уравнение относительно у:
Слайд 33Пример 6.
Определить тип кривой и схематически построить ее
Решение. Приведем заданное уравнение
Слайд 40Пример 5. Вычислить предел
Сначала попробуем подставить -1 в дробь:
В данном случае
Общее правило: если в числителе и знаменателе находятся многочлены, и имеется неопределенность вида 0/0, то для ее раскрытия нужно разложить числитель и знаменатель на множители.
Очевидно, что можно сократить на (х+1)
:
Теперь и подставляем -1 в выражение, которое осталось под знаком предела:
Слайд 41Пример 6.
Найти предел
Сначала пробуем подставить 3 в выражение под знаком предела
Когда в числителе (знаменателе) находится разность корней (или корень минус какое-нибудь число), то для раскрытия неопределенности используют метод умножения числителя и знаменателя на сопряженное выражение.
Получена неопределенность вида 0/0 , которую нужно устранять
Слайд 44Пример 9. Вычислить предел
Решение.
Пример 10. Вычислить предел
Решение. Преобразуем числитель
Слайд 45Производная функции
Пример 1. Вычислить первую и вторую производную, дифференциал функции
Решение
Слайд 50Пример 5. Исследовать функцию g(x) и построить ее график
Область определения -
Функция непериодическая.
Четность/нечетность - функция общего вида.
Точки пересечения с осью ОХ: y = 0 x = 2
c осью OY: х = 0 ; у=-10\е ;
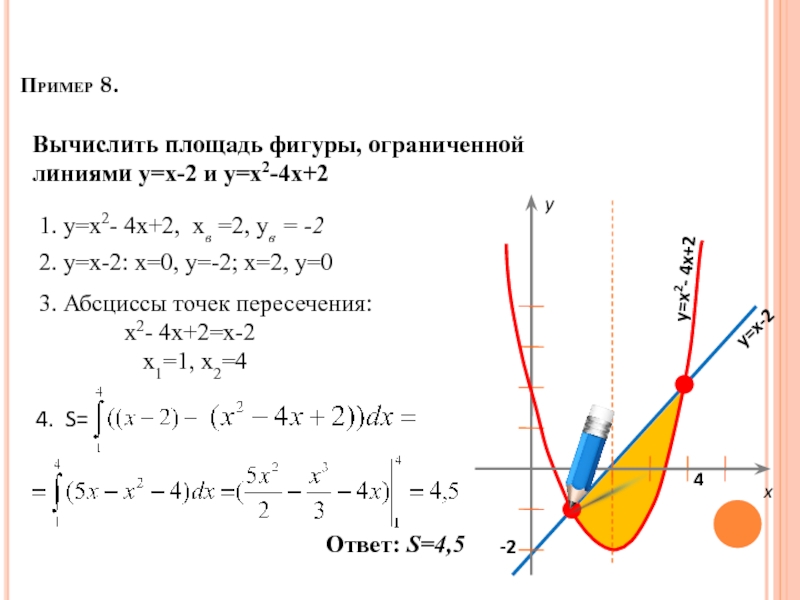
Слайд 61Пример 8.
Вычислить площадь фигуры, ограниченной
линиями y=x-2 и y=x2-4x+2
1. y=x2-
3. Абсциссы точек пересечения:
x2- 4x+2=x-2
х1=1, х2=4
4. S=
Ответ: S=4,5
2. у=х-2: х=0, у=-2; х=2, у=0