Содержание лекции:
Формулировка общей задачи математического программирования
Классификация задач нелинейного программирования
Понятие о функции Лагранжа
Теорема Куна-Таккера. Интерпретация множителей Лагранжа
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 7. Постановка задачи нелинейного программирования. Теорема Куна-Таккера презентация
Содержание
- 1. Лекция 7. Постановка задачи нелинейного программирования. Теорема Куна-Таккера
- 2. Постановка задачи нелинейного программирования. Теорема Куна-Таккера (с)
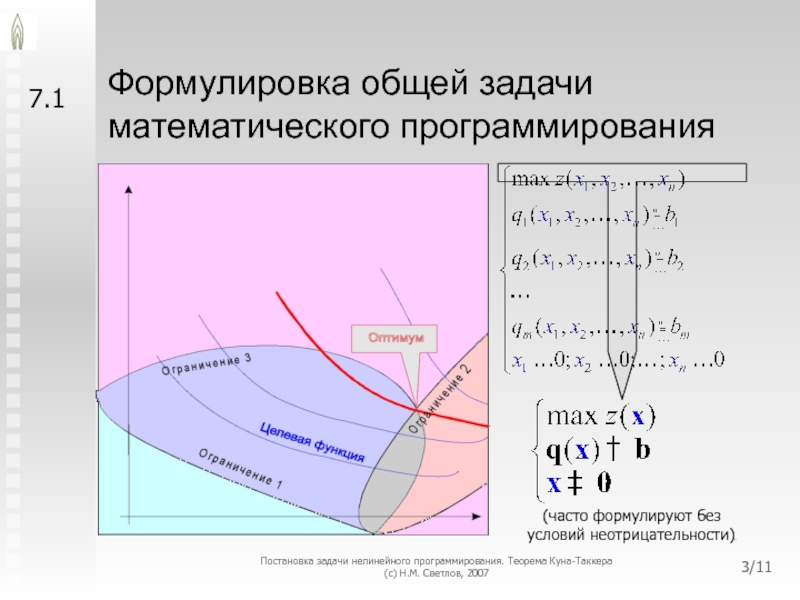
- 3. Формулировка общей задачи математического программирования 7.1
- 4. 7.1 Постановка задачи нелинейного программирования. Теорема Куна-Таккера (с) Н.М. Светлов, 2007 /11
- 5. 7.2 Постановка задачи нелинейного программирования. Теорема Куна-Таккера (с) Н.М. Светлов, 2007 Повторение /11
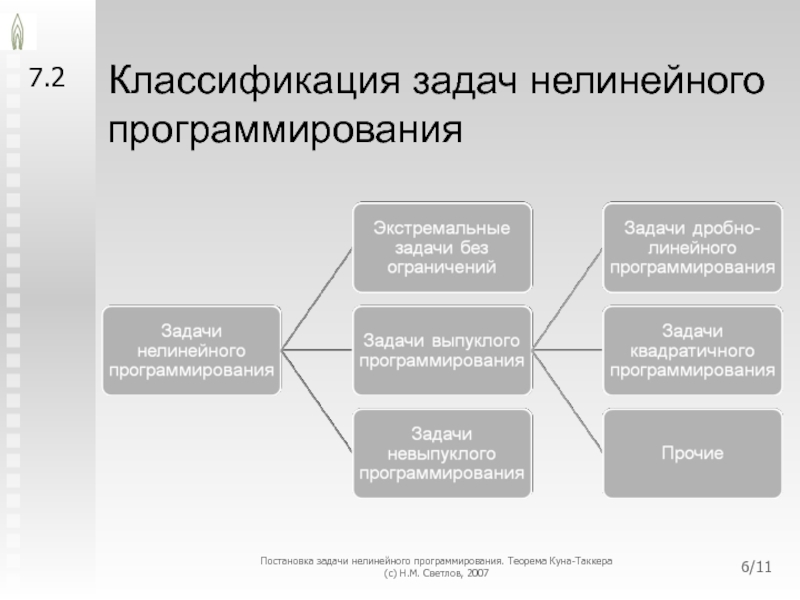
- 6. Классификация задач нелинейного программирования 7.2 Постановка задачи
- 7. Понятие о функции Лагранжа Решение любой задачи
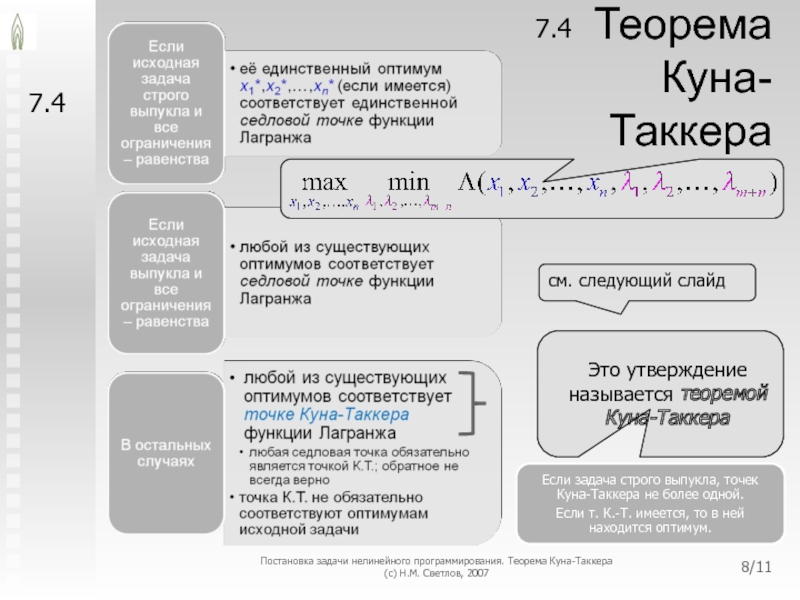
- 8. Теорема Куна-Таккера 7.4 Постановка задачи нелинейного программирования.
- 9. 7.4 Точка Куна-Таккера (x1*,x2*,…,xn*,λ1*, λ2*, …, λт+n*)
- 10. 7.4 Переменные λi называются множителями Лагранжа.
- 11. 7.4 Теорема Куна-Таккера используется для аналитического отыскания
Постановка задачи нелинейного программирования. Теорема Куна-Таккера
(с) Н.М. Светлов, 2007 /11 Литература Шелобаев С.И. Экономико-математические методы и модели: Учеб. пособие для вузов. — 2-е изд. М.: ЮНИТИ-ДАНА, 2005. — Разделы 4.1
Слайд 1Постановка задачи нелинейного программирования. Теорема Куна-Таккера
(с) Н.М. Светлов, 2007
Лекция 7. Постановка
задачи нелинейного программирования. Теорема Куна-Таккера
Слайд 2Постановка задачи нелинейного программирования. Теорема Куна-Таккера
(с) Н.М. Светлов, 2007
/11
Литература
Шелобаев С.И. Экономико-математические
методы и модели: Учеб. пособие для вузов. — 2-е изд. М.: ЮНИТИ-ДАНА, 2005. — Разделы 4.1 (до начала подраздела «Аналитические методы решения задач условной оптимизации»), 4.2.
Исследование операций в экономике: Учебн. пособие для вузов / Под ред. Н.Ш. Кремера. М.: Банки и биржи, ЮНИТИ, 1997. — Разделы 10.2, 11.2.
Исследование операций в экономике: Учебн. пособие для вузов / Под ред. Н.Ш. Кремера. М.: Банки и биржи, ЮНИТИ, 1997. — Разделы 10.2, 11.2.
Слайд 3
Формулировка общей задачи математического программирования
7.1
Постановка задачи нелинейного программирования. Теорема Куна-Таккера
(с) Н.М.
Светлов, 2007
(часто формулируют без условий неотрицательности)
/11
Слайд 47.1
Постановка задачи нелинейного программирования. Теорема Куна-Таккера
(с) Н.М. Светлов, 2007
/11
Слайд 57.2
Постановка задачи нелинейного программирования. Теорема Куна-Таккера
(с) Н.М. Светлов, 2007
Повторение
/11
Слайд 6Классификация задач нелинейного программирования
7.2
Постановка задачи нелинейного программирования. Теорема Куна-Таккера
(с) Н.М. Светлов,
2007
/11
Слайд 7Понятие о функции Лагранжа
Решение любой задачи математического программирования (в том числе
нелинейного) можно свести к решению задачи нелинейного программирования без ограничений.
Для этого необходимо на основе исходной ЗМП построить функцию Лагранжа:
Для этого необходимо на основе исходной ЗМП построить функцию Лагранжа:
7.3
Постановка задачи нелинейного программирования. Теорема Куна-Таккера
(с) Н.М. Светлов, 2007
В отсутствие условий неотрицательности:
/11
Слайд 8Теорема Куна-Таккера
7.4
Постановка задачи нелинейного программирования. Теорема Куна-Таккера
(с) Н.М. Светлов, 2007
см. следующий
слайд
7.4
/11
Слайд 97.4
Точка Куна-Таккера
(x1*,x2*,…,xn*,λ1*, λ2*, …, λт+n*) определяется следующими условиями ?
Постановка задачи нелинейного
программирования. Теорема Куна-Таккера
(с) Н.М. Светлов, 2007
/11
Слайд 107.4
Переменные λi называются множителями Лагранжа.
Экономическая интерпретация множителей Лагранжа, соответствующих оптимальному решению,
аналогична интерпретации двойственных оценок ограничений ЗЛП
Они показывают величину изменения целевой функции в расчёте на единицу изменения свободного члена ограничения, которому соответствует множитель Лагранжа, в очень малой окрестности оптимума
Если ограничение можно рассматривать в качестве баланса ресурса и максимизируется прибыль, то множитель Лагранжа в точке оптимума равен оптимальной цене
Если найдётся рынок, где ресурс дешевле, то его покупка увеличит прибыль
Если найдётся рынок, где ресурс дороже, то для увеличения прибыли его следует продать
В отличие от случая ЗЛП, множители Лагранжа (кроме частных случаев) не обладают свойством устойчивости
Они меняют свои значения даже при сколь угодно малом изменении свободных членов ограничений
Они показывают величину изменения целевой функции в расчёте на единицу изменения свободного члена ограничения, которому соответствует множитель Лагранжа, в очень малой окрестности оптимума
Если ограничение можно рассматривать в качестве баланса ресурса и максимизируется прибыль, то множитель Лагранжа в точке оптимума равен оптимальной цене
Если найдётся рынок, где ресурс дешевле, то его покупка увеличит прибыль
Если найдётся рынок, где ресурс дороже, то для увеличения прибыли его следует продать
В отличие от случая ЗЛП, множители Лагранжа (кроме частных случаев) не обладают свойством устойчивости
Они меняют свои значения даже при сколь угодно малом изменении свободных членов ограничений
Постановка задачи нелинейного программирования. Теорема Куна-Таккера
(с) Н.М. Светлов, 2007
/11
Слайд 117.4
Теорема Куна-Таккера используется для аналитического отыскания оптимума задачи нелинейного программирования
Впрочем, этот
приём приводит к успешным результатам отнюдь не для любой задачи
Главное, чем полезна теорема Куна-Таккера:
выяснение роли множителей Лагранжа в формулировании условий оптимальности
экономическая интерпретация множителей Лагранжа
Главное, чем полезна теорема Куна-Таккера:
выяснение роли множителей Лагранжа в формулировании условий оптимальности
экономическая интерпретация множителей Лагранжа
Постановка задачи нелинейного программирования. Теорема Куна-Таккера
(с) Н.М. Светлов, 2007
/11
