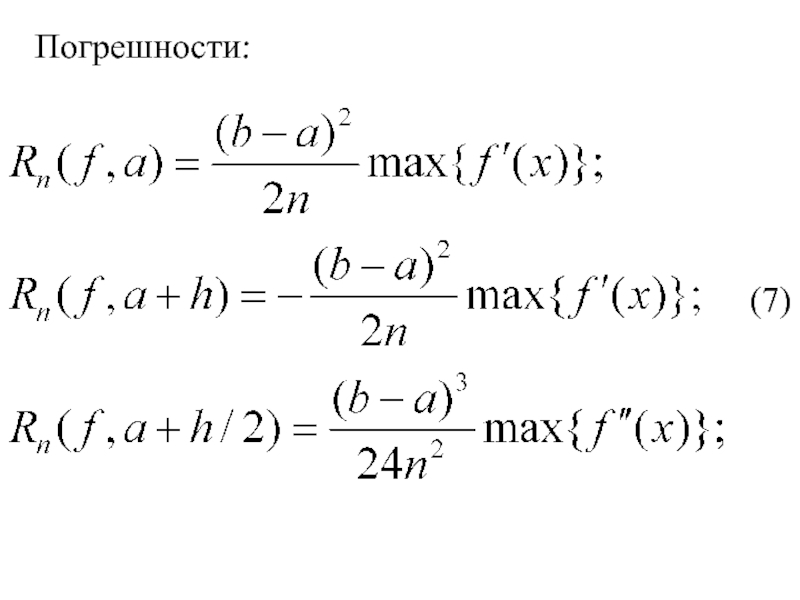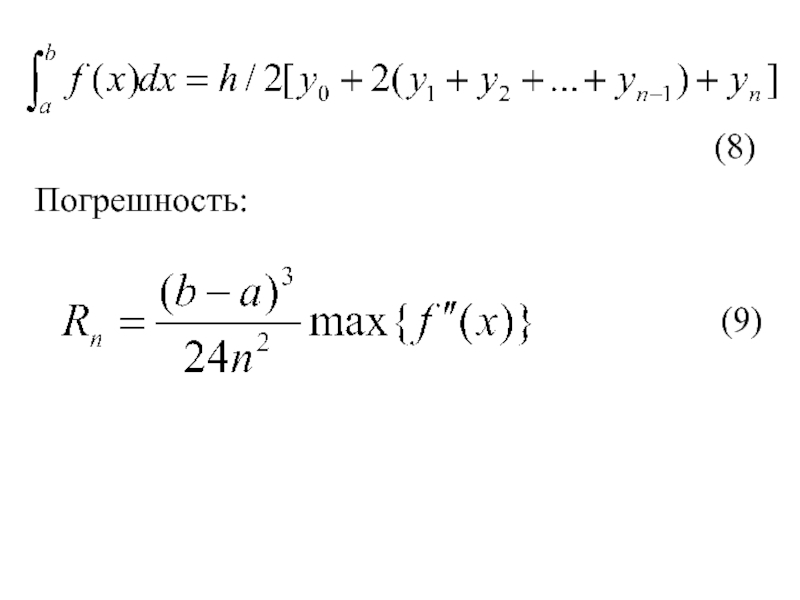интегрирования.
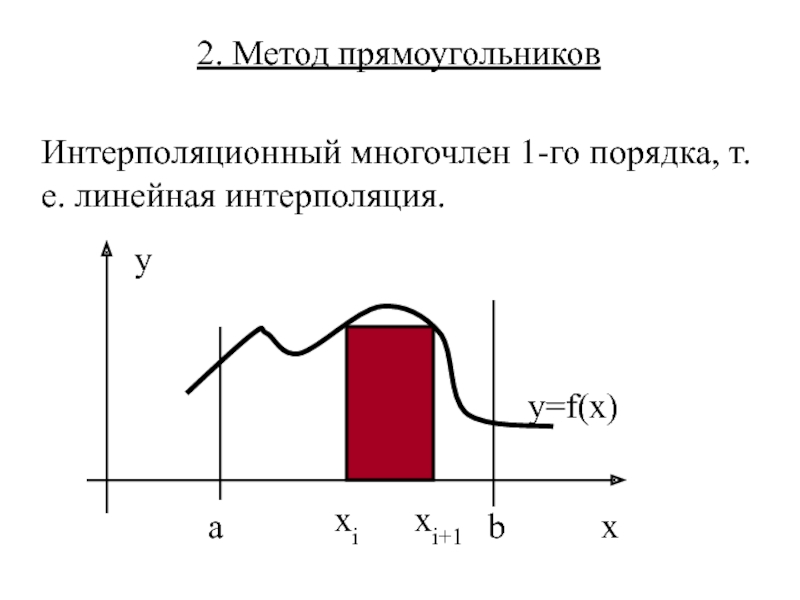
2. Метод прямоугольников.
3. Метод трапеций.
4. Численное интегрирование методом Симпсона.
Литература: [1] с.123-134.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 6. Методы численного интегрирования презентация
Содержание
- 1. Лекция 6. Методы численного интегрирования
- 2. 1. Обзор методов численного нтегрирования Задача численного
- 3. Методы сплайн – интегрирования основаны на аппроксимации
- 4. Методы Ньютона-Котеса предусматривают разбиение интервала интегрирования [a,b]
- 5. 2. Метод прямоугольников Интерполяционный многочлен 1-го порядка, т.е. линейная интерполяция.
- 6. (6) Если узел α=а- левому краю отрезка
- 7. (7) Погрешности:
- 8. 3. Метод трапеций Интерполяционный многочлен 1-го порядка, т.е. линейная интерполяция.
- 9. (8) Погрешность: (9)
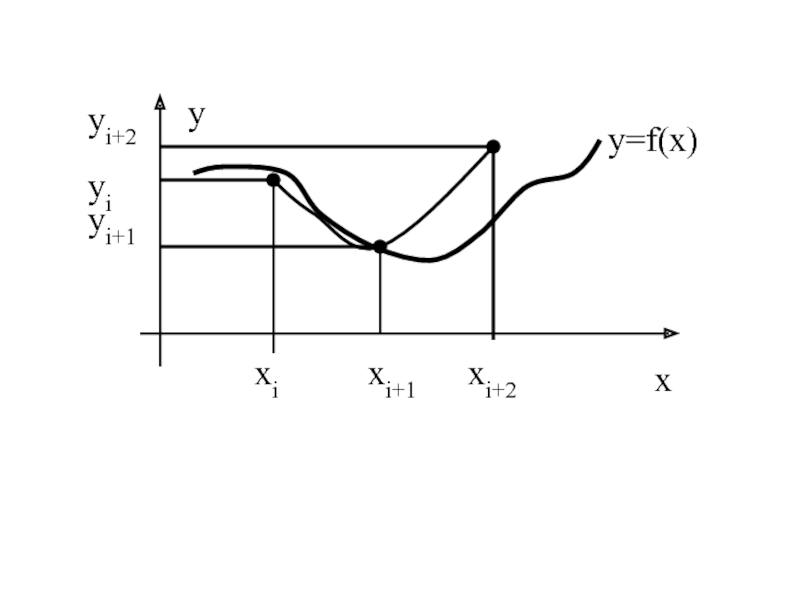
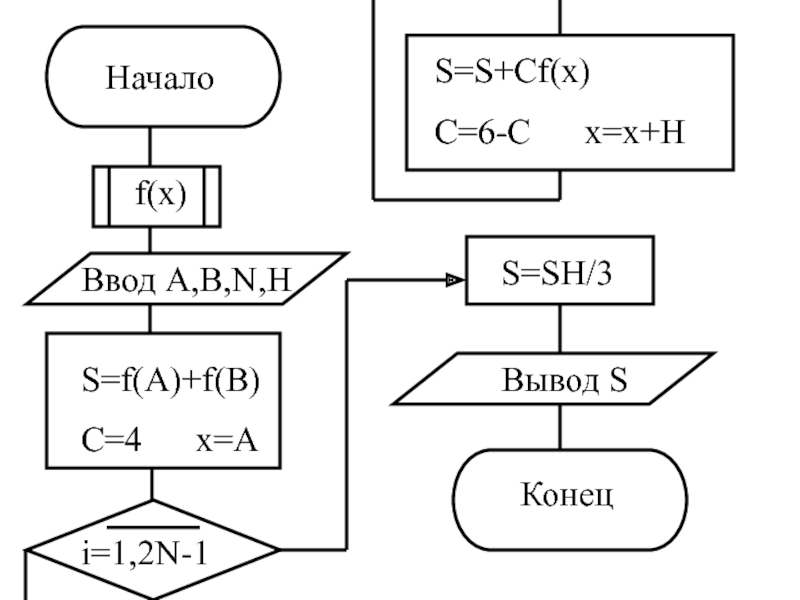
- 10. 4. Метод Симпсона. Описание метода.
- 11. y x y=f(x) xi xi+1 yi+1 yi xi+2 yi+2
- 12. Погрешность метода Симпсона: где: (3)
Слайд 1Тема 2. Численное интегрирование
Лекция 6. Методы численного интегрирования.
1.Обзор методов численного
Слайд 21. Обзор методов численного нтегрирования
Задача численного интегрирования-
вычислить интеграл
используя
ряд значений подинтегральной функции y=f(x), которые известны заранее.
Методы численного интегрирования:
Методы Ньютона-Котеса – основаны на аппроксимации подинтегральной функции полиномами степени n при равноотстоящих друг от друга узлах;
ряд значений подинтегральной функции y=f(x), которые известны заранее.
Методы численного интегрирования:
Методы Ньютона-Котеса – основаны на аппроксимации подинтегральной функции полиномами степени n при равноотстоящих друг от друга узлах;
Слайд 3Методы сплайн – интегрирования основаны на аппроксимации подинтегральной функции сплайнами –
функциями, форма которых близка к интегрируемой функции;
Метод Гаусса использует специально выбираемые неравноотстоящие узлы, что обеспечивает высокую точность вычислений;
Метод Монте-Карло используется для вычисления кратных интегралов на случайно выбираемых узлах; результат является случайной величиной и определяется с заданной вероятностью.
Метод Гаусса использует специально выбираемые неравноотстоящие узлы, что обеспечивает высокую точность вычислений;
Метод Монте-Карло используется для вычисления кратных интегралов на случайно выбираемых узлах; результат является случайной величиной и определяется с заданной вероятностью.
Слайд 4Методы Ньютона-Котеса предусматривают разбиение интервала интегрирования [a,b] на n равных частей
с шагом:
h=xi+1- xi=(b-a)/n, i=1,n (4)
При этом известны в узлах разбиения значения подинтегральной функции известны:
yi=f(xi) (5)
h=xi+1- xi=(b-a)/n, i=1,n (4)
При этом известны в узлах разбиения значения подинтегральной функции известны:
yi=f(xi) (5)
Слайд 6(6)
Если узел α=а- левому краю отрезка интегрирования, то (6) – формула
«левых» прямоугольников;
Если узел α=xi+1 –правому краю отрезка, то (6) – формула «правых» прямоугольников;
Если узел α=(xi+1+xi)/2 – середине отрезка то (6) – формула «средних» прямоугольников;
Если узел α=xi+1 –правому краю отрезка, то (6) – формула «правых» прямоугольников;
Если узел α=(xi+1+xi)/2 – середине отрезка то (6) – формула «средних» прямоугольников;
Слайд 10
4. Метод Симпсона.
Описание метода.
(1)
При этом, необходимым условием является то, что
количество интервалов разбиения отрезка интегрирования должно быть четным.
(2)
