- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ЛА-УП-Л6 презентация
Содержание
- 1. ЛА-УП-Л6
- 2. План лекции Определение линейного подпространства n-мерного координатного
- 3. Векторные подпространства. Определение Подпространством линейного пространства Rnнад
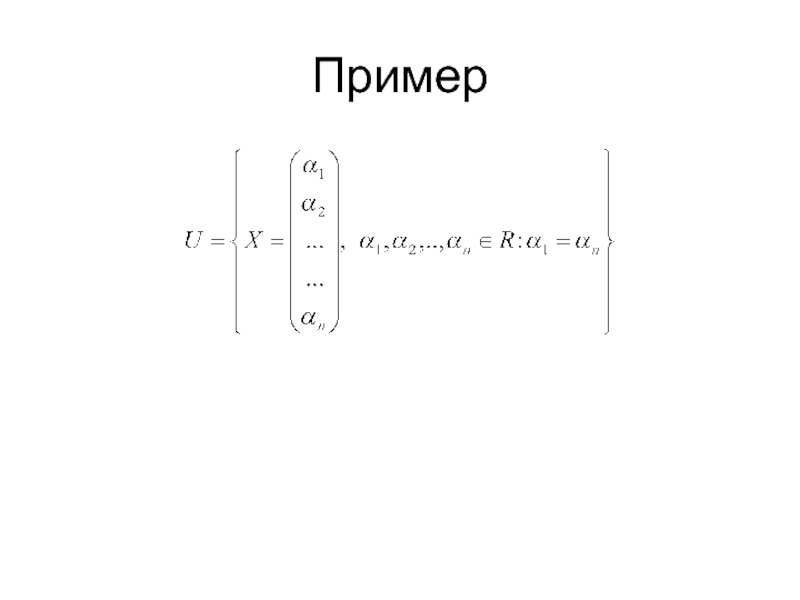
- 4. Пример
- 5. Векторные подпространства. Способ задания Подпространством, порождённым
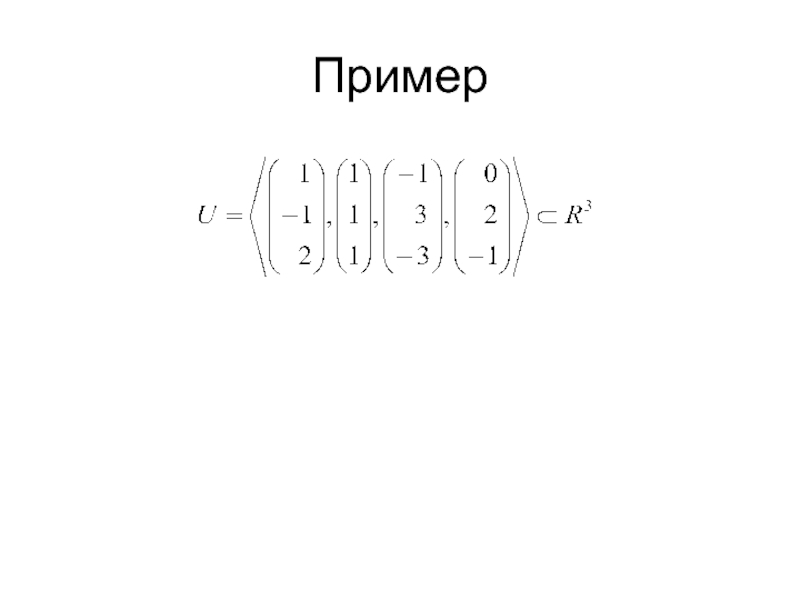
- 6. Пример
- 7. Векторные подпространства. Способ задания Другой способ
- 8. Пример
- 9. Базис векторного пространства. Определение Пусть
- 10. Размерность векторного пространства Все базисы
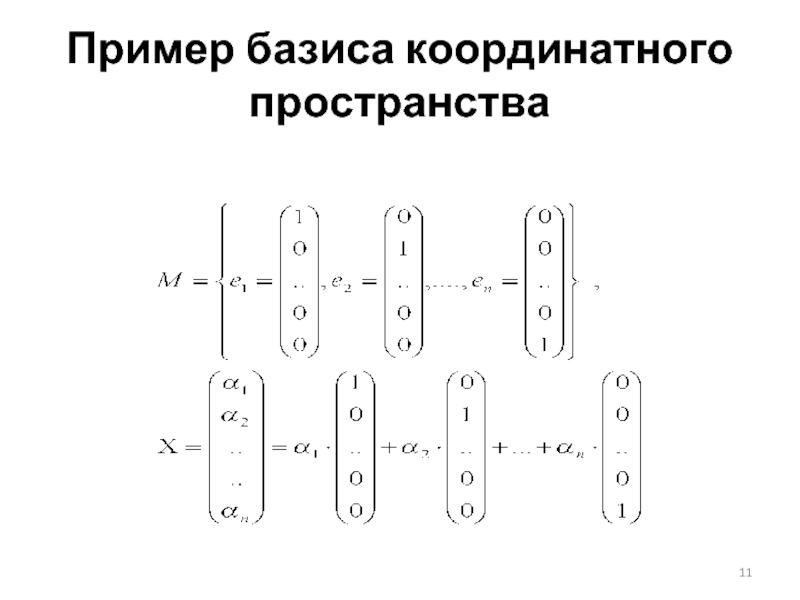
- 11. Пример базиса координатного пространства
- 12. Теоремы о базисах В любом ненулевом подпространстве
- 13. 18.11.2015 Векторные пространства
- 14. Алгоритм построения базиса в
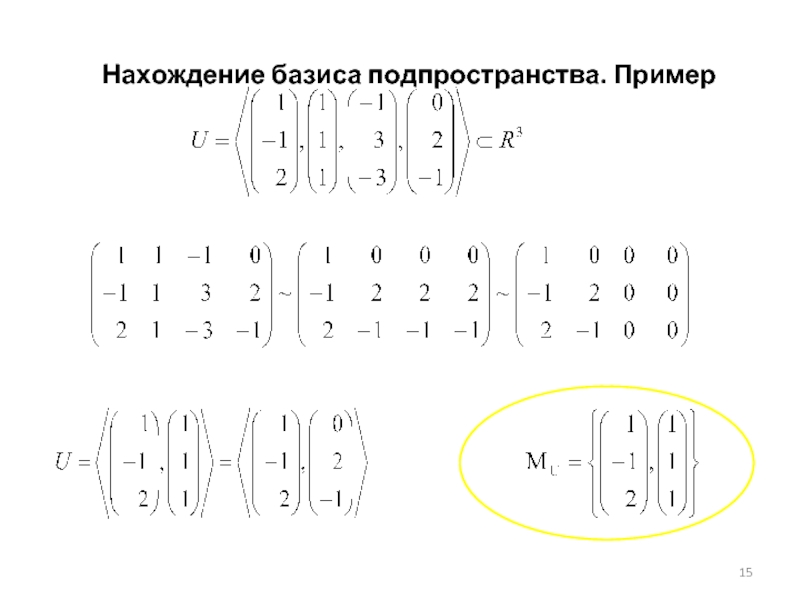
- 15. Нахождение базиса подпространства. Пример
- 16. Нахождение базиса подпространства. Пример
- 17. Координаты вектора в базисе Пусть
- 21. 1. Вычислим скалярное произведение (e1,e2):
- 22. Построение ортогонального базиса (продолжение)
- 23. Построение ортогонального базиса (продолжение)
Слайд 2План лекции
Определение линейного подпространства n-мерного координатного пространства
Линейная оболочка набора векторов
Линейное пространство
Базис и размерность
Ортонормированные базисы
Слайд 3Векторные подпространства. Определение
Подпространством линейного пространства Rnнад полем Rназывают такое подмножество
.
Другими словами, подмножество U замкнуто относительно действий «сложения» и «умножения» на скаляр, определённых в Rn.
Тривиальными подпространствами линейного пространства Rn называются само Rn и пространство, состоящее из одного нулевого вектора O.
Слайд 5Векторные подпространства. Способ задания
Подпространством, порождённым векторами
называют подмножество всех линейных комбинаций этих векторов (линейная оболочка набора векторов), т.е.
Слайд 7Векторные подпространства. Способ задания
Другой способ задания линейного подпространства в Rn
Теорема. Множество решений однородной системы уравнений A⋅X = O образует линейное подпространство пространства Rn .
Слайд 9Базис векторного пространства. Определение
Пусть
называется базисом в Q, если :
а)
б) система линейно независима;
в) для любого найдутся такие числа , что
Слайд 10 Размерность векторного пространства
Все базисы
имеют одинаковое число векторов, которое называется размерностью векторного пространства V и обозначается
Полагают, что размерность тривиального пространства (состоящего из одного только нулевого вектора), равна нулю: dim(O)= 0.
Размерность подпространства, заданного СЛУ, равна n – rg(A).
Слайд 12Теоремы о базисах
В любом ненулевом подпространстве координатного пространства существует базис.
Если размерность
Слайд 1318.11.2015
Векторные пространства
Нахождение базиса подпространства
Для нахождения базиса в подпространстве, порожденном
Например,
Слайд 14
Алгоритм построения базиса в
Столбцы, порождающие подпространство, записать в матрицу.
Элементарными преобразованиями
Ненулевые столбцы данной «ступенчатой» матрицы и будут составлять базис исходного подпространства, а ранг матрицы будет равен размерности этого подпространства.
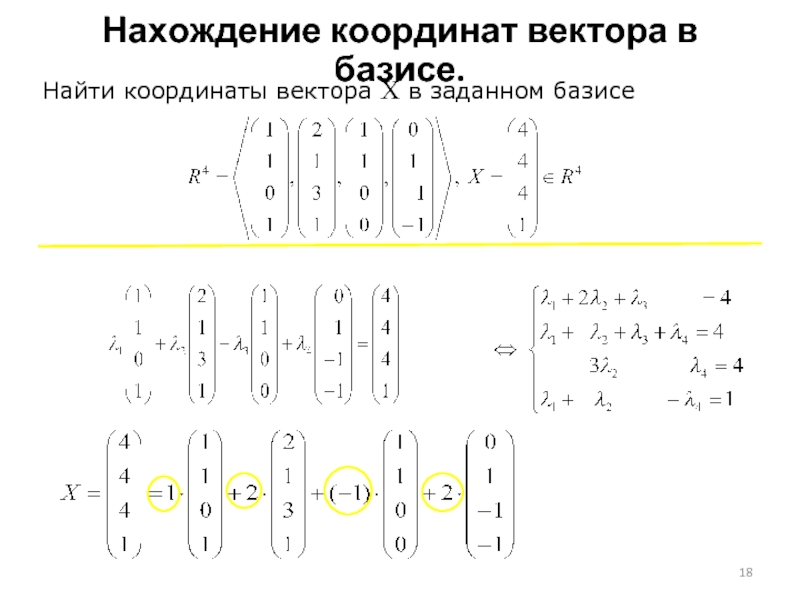
Слайд 17 Координаты вектора в базисе
Пусть даны
Координатами вектора Х в этом базисе называют коэффициенты в разложении:
Слайд 19
Определение.
Базис
Другими словами,
ортогональным базисом называется базис, состоящий из попарно ортогональных векторов.
Ортогональный базис
Слайд 20
Определение.
Базис
Другими словами,
ортонормированным базисом называется базис, состоящий из попарно ортогональных векторов, каждый из которых имеет длину, равную единице.
Ортонормированный базис
Слайд 211. Вычислим скалярное произведение (e1,e2):
2. Задача сводится к построению векторов e3 и e4 таких, что e3⊥e4 и оба ортогональны e1, e2 .
Построение ортогонального базиса
Задача.
Проверить ортогональность системы векторов
и дополнить ее до ортогонального базиса в R4 .
Слайд 22Построение ортогонального базиса (продолжение)
Для определения
частное решение системы
Выберем частное решение
Слайд 23Построение ортогонального базиса (продолжение)
Для определения
решение системы
Общее решение - , выберем