- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Кривые второго порядка презентация
Содержание
- 1. Кривые второго порядка
- 2. Кривые второго порядка Ax2 + 2Bxy +
- 3. Эллипс Декартово уравнение: x2/a2 + y2/b2 =
- 4. Окружность Декартово уравнение: x2 + y2
- 5. Парабола Декартово уравнение: y = ax2 + bx + c
- 7. Гипербола Декартово уравнение: x2/a2 -
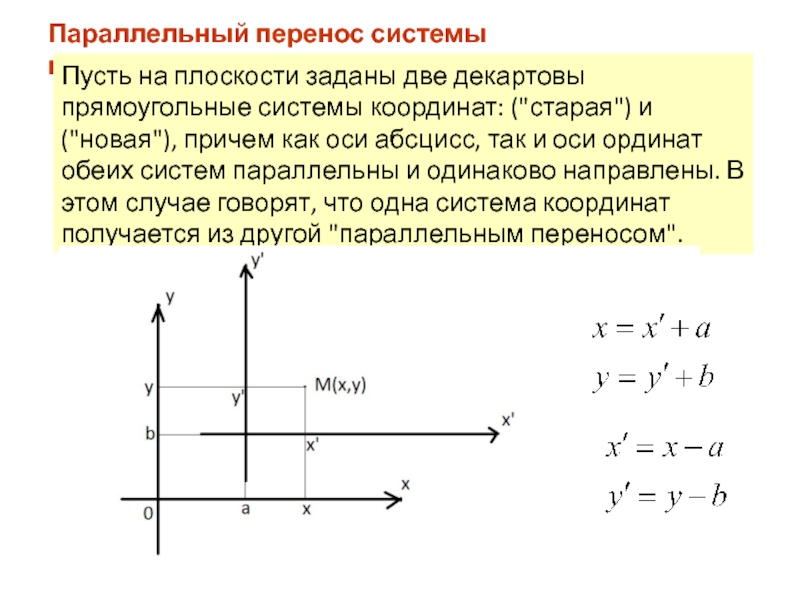
- 10. Параллельный перенос системы координат
- 11. Преобразование уравнения кривой при параллельном переносе Ax2
- 12. Преобразование уравнения кривой при параллельном переносе Подберем
- 13. 1 случай. Преобразование уравнения кривой при параллельном
- 14. По часовой стрелке
- 15. Против часовой стрелки
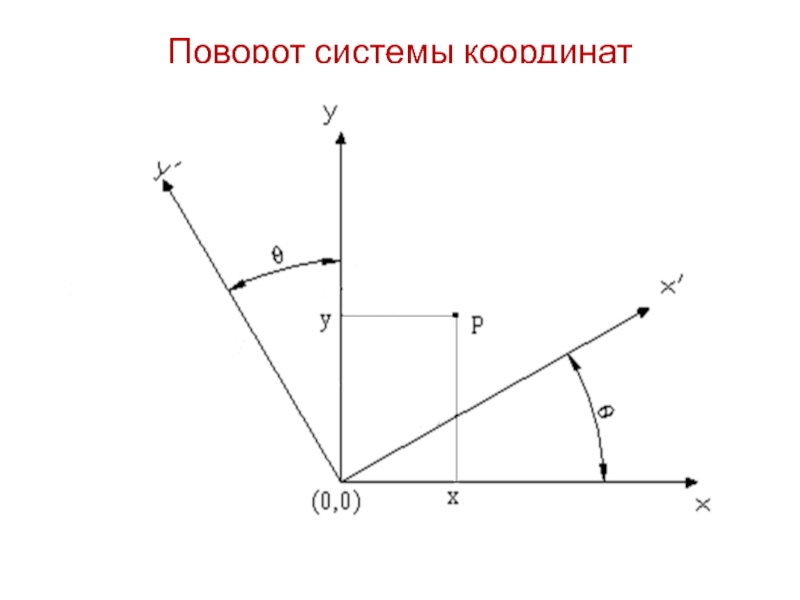
- 16. Поворот системы координат
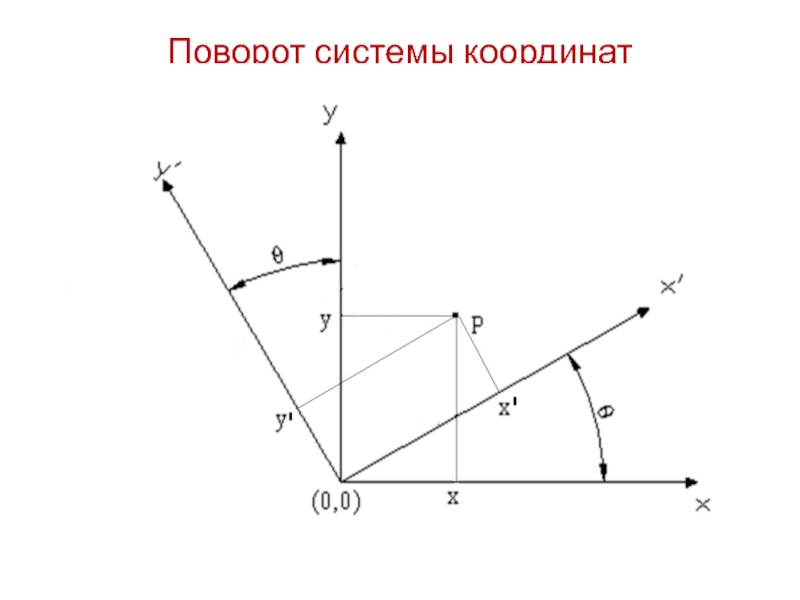
- 17. Поворот системы координат
- 18. где есть матрица поворота (ортогональная матрица) Поворот системы координат
- 19. 1 случай. Преобразование уравнения кривой при повороте
- 20. Как найти θ Пример.
- 21. Классификация центральных кривых (
- 22. Классификация центральных кривых (
- 23. Преобразование общего уравнения к каноническому виду (пример)
- 24. Преобразование общего уравнения к каноническому виду (пример)
- 25. 2 случай. Преобразование уравнения кривой Ax2
- 26. Классификация нецентральных кривых (
Слайд 2Кривые второго порядка
Ax2 + 2Bxy + Cy2 - главная часть
2Dx + 2Ey + F - линейная часть уравнения
Слайд 3Эллипс
Декартово уравнение: x2/a2 + y2/b2 = 1
Параметрическое уравнение:
x =
Слайд 4Окружность
Декартово уравнение: x2 + y2 = a2
Параметрическое уравнение:
x
Слайд 7Гипербола
Декартово уравнение:
x2/a2 - y2/b2 = 1
Параметрическое уравнение:
x
Слайд 11Преобразование уравнения кривой при параллельном переносе
Ax2 + 2Bxy + Cy2 +
Подставляем
Главная часть не меняется, можно упростить только
линейную часть
Слайд 12Преобразование уравнения кривой при параллельном переносе
Подберем a и b в
так,
стали равными 0:
Для нахождения a и b получили систему уравнений,
которая имеет единственное решение при условии
Слайд 131 случай. Преобразование уравнения кривой при параллельном переносе при
Преобразованное уравнение:
Таким образом, в новой системе координат уравнение принимает вид
Ax2 + 2Bxy + Cy2 + F= 0
Для дальнейшего упрощения повернем систему координат.
Слайд 191 случай. Преобразование уравнения кривой при повороте при
Преобразованное уравнение:
Главная часть уравнения – квадратичная форма,
а преобразование – ортогональное – приведение к главным осям.
Тогда после подстановки в уравнение получаем
Ax2 + 2Bxy + Cy2 + F= 0
Слайд 21Классификация центральных кривых (
Преобразованное уравнение:
Уравнения для нахождения коэффициентов при квадратах:
Слайд 22Классификация центральных кривых (
Вырожденные центральные кривые
Невырожденные центральные кривые
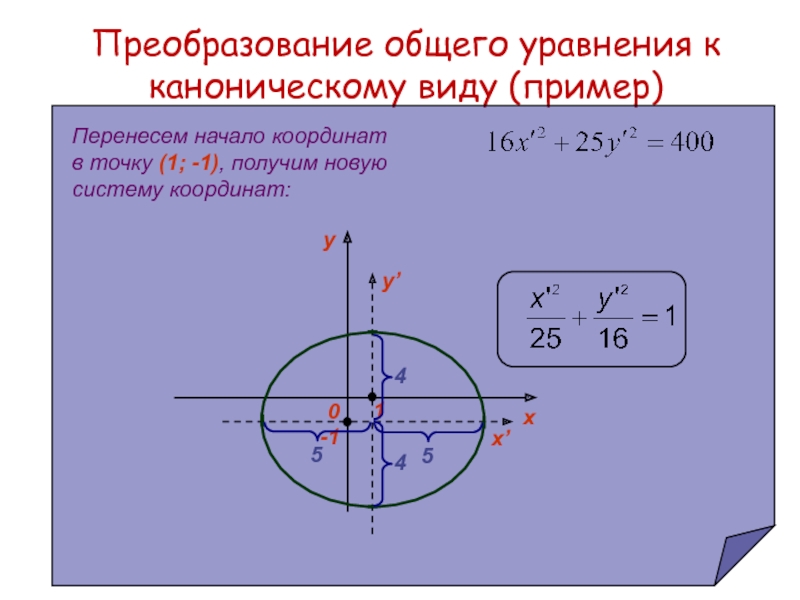
Слайд 24Преобразование общего уравнения к каноническому виду (пример)
-1
1
y’
x’
Перенесем начало координат в точку
Слайд 252 случай. Преобразование уравнения кривой Ax2 + 2Bxy + Cy2 +
Сразу производим поворот
Так как , остается только один квадрат, например, для y:
Для дальнейшего упрощения (предполагаем D,F ненулевые)
Слайд 26Классификация нецентральных кривых (
Вырожденные нецентральные кривые
Невырожденные нецентральные кривые
Преобразованное уравнение: