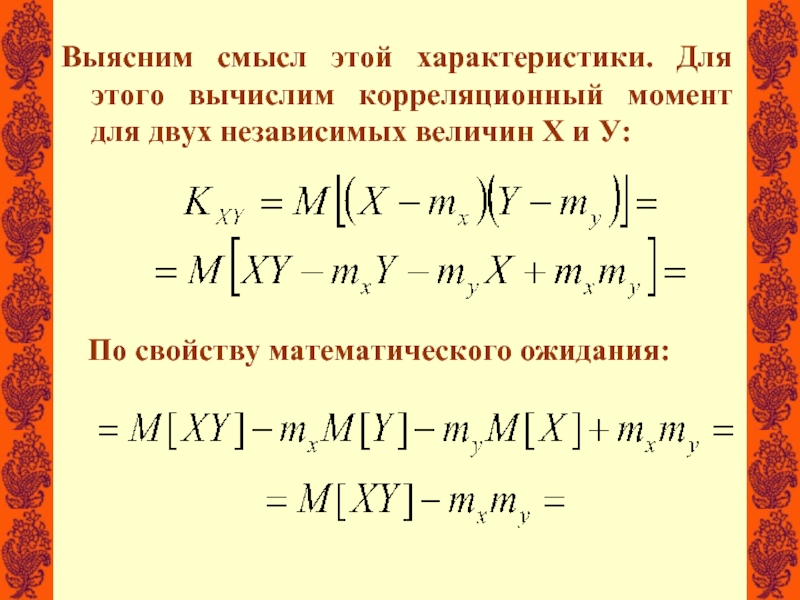- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Корреляция случайных величин презентация
Содержание
- 1. Корреляция случайных величин
- 2. Для дискретных СВ он выражается формулой: А для непрерывных СВ:
- 3. Выясним смысл этой характеристики. Для этого вычислим
- 4. Корреляционный момент двух независимых величин равен
- 5. Следовательно, если корреляционный момент двух случайных величин
- 6. коэффициент корреляции
- 7. Для независимых СВ он также равен нулю.
- 8. Вычислим коэффициент корреляции для СВ Х и У из предыдущего примера.
- 9. Коэффициент корреляции характеризует не всякую, а только
- 10. Вычислим корреляционный момент случайных величин Х и У: По свойству математического ожидания:
- 11. Выражение, стоящее в скобках, по определению является
- 12. Таким образом, знак коэффициента корреляции определяется
- 13. Найдем дисперсию Z: (т.к. дисперсия всегда неотрицательна). Тогда
- 14. Следовательно, Если случайные величины положительно коррелированы,
Слайд 1Ранее было введено понятие корреляционного момента двух случайных величин:
28. КОРРЕЛЯЦИЯ СЛУЧАЙНЫХ
Слайд 3Выясним смысл этой характеристики. Для этого вычислим корреляционный момент для двух
По свойству математического ожидания:
Слайд 4Корреляционный момент двух
независимых величин равен нулю.
Математическое ожидание произведения независимых случайных
М[XY]=M[X]M[Y]
Следовательно,
Слайд 5Следовательно, если корреляционный момент двух случайных величин отличен от нуля, то
Из определения корреляционного момента следует, что если одна из величин мало отклоняется от своего мат. ожидания (почти не случайна), то момент будет небольшим, какой бы тесной не была зависимость.
Поэтому для характеристики связи между величинами Х и У переходят к безразмерной величине:
Слайд 7Для независимых СВ он также равен нулю. Такие СВ называются некоррелированными.
Некорреляция
Если Kxy>0, то СВ называются положительно
коррелированными.
Если Kxy<0, то СВ называются отрицательно
коррелированными.
Слайд 9Коэффициент корреляции характеризует не всякую, а только линейную зависимость, при которой
Коэффициент корреляции характеризует степень тесноты линейной зависимости между СВ.
Пусть
У=AХ+B
где А и В – постоянные.
Слайд 10Вычислим корреляционный момент случайных величин Х и У:
По свойству математического ожидания:
Слайд 11Выражение, стоящее в скобках, по определению является дисперсией Х:
С другой стороны,
Тогда
Следовательно
Слайд 12
Таким образом, знак коэффициента корреляции определяется знаком постоянной А.
Далее, чтобы показать,
Слайд 14
Следовательно,
Если случайные величины положительно коррелированы, то возрастанию одной из них соответствует
Если корреляция отрицательная, то возрастанию одной СВ соответствует убывание другой (например, время, потраченное студентом на подготовку к контрольной и количество сделанных им в работе ошибок).