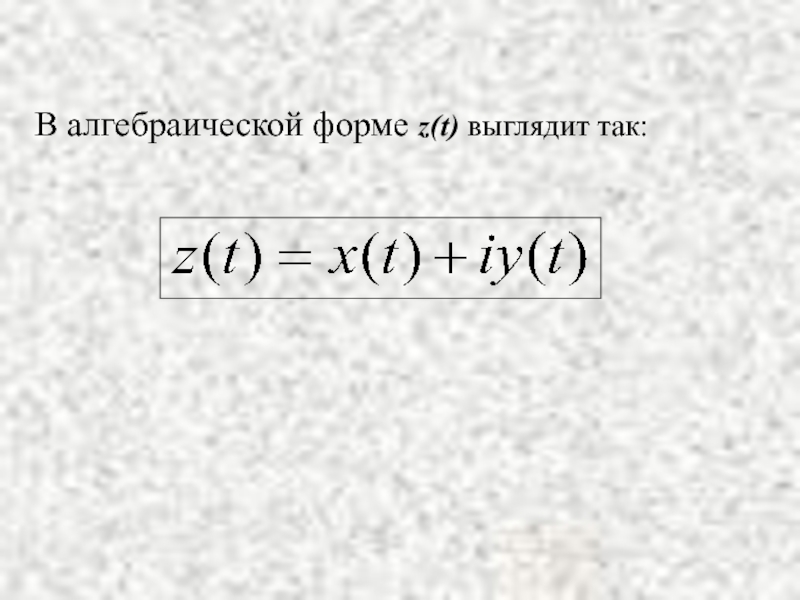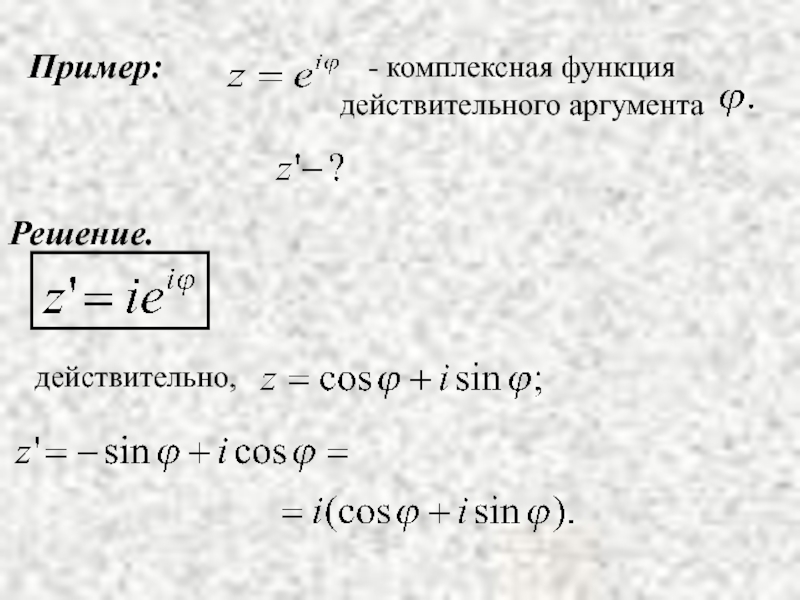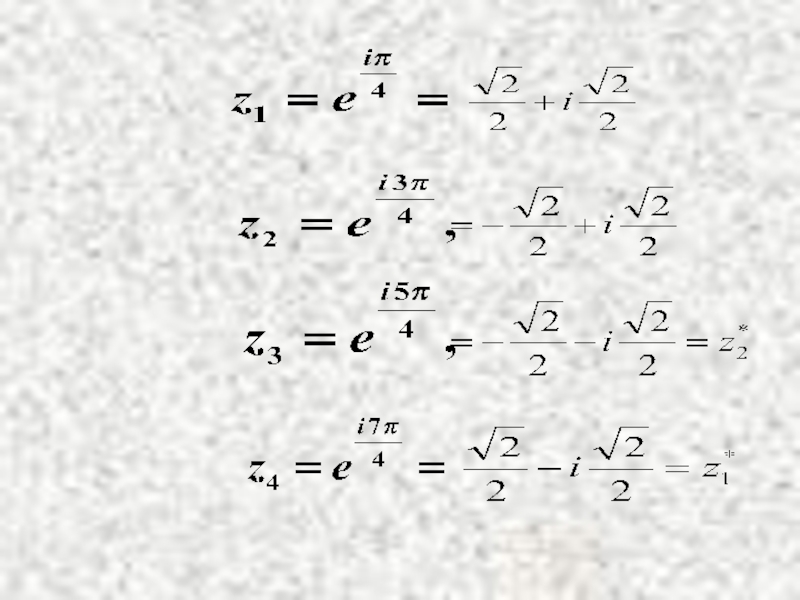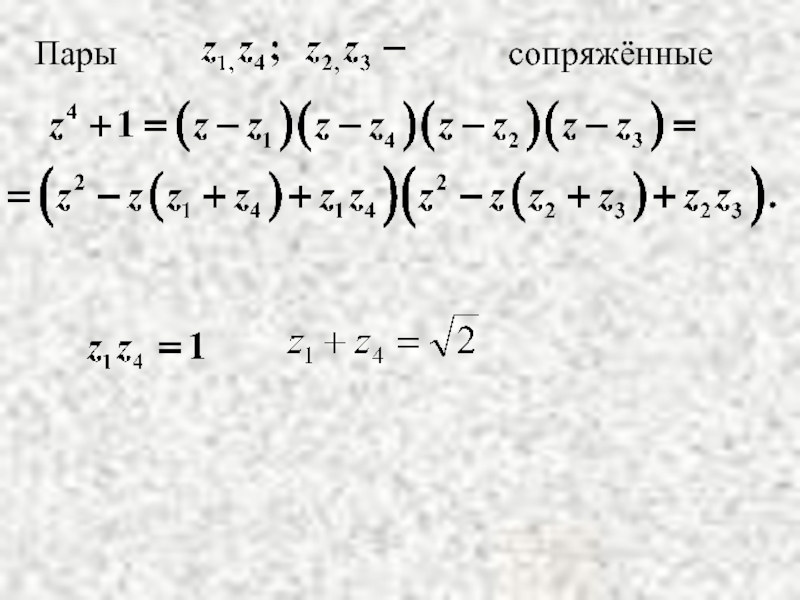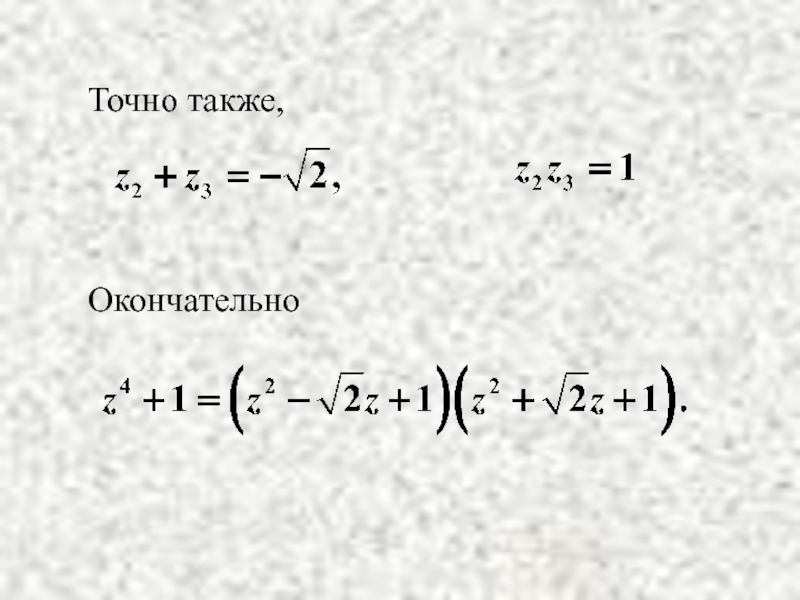- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Комплексные функции и многочлены презентация
Содержание
- 1. Комплексные функции и многочлены
- 2. Лекция 4 2. Многочлены в комплексной
- 4. В алгебраической форме z(t) выглядит так:
- 5. Отсюда, в частности, следует правило дифференцирования комплексной функции:
- 6. Пример: Решение. действительно,
- 7. Рассмотрим многочлен порядка n: Здесь z - комплексная переменная.
- 9. Как и в элементарной алгебре справедливо основное свойство деления: Здесь:
- 10. Корни многочлена ( деление без остатка)
- 11. В развернутом виде: Такое уравнение называется алгебраическим уравнением n-ой степени. Теорема Безу.
- 12. Доказательство. По условию: По основному свойству деления: Пложим z = a, тогда
- 13. Следствие. и т.д.
- 15. Основная теорема алгебры Многочлен n-ой
- 16. Таким образом: Комплексные корни многочлена с действительными коэффициентами являются сопряженными парами корней .
- 17. Из теоремы Безу и основной теоремы алгебры
- 18. Здесь …………………………..
- 19. 1. Линейные множители - соответствуют действительным корням
- 20. Для доказательства последнего рассмотрим: Здесь:
- 21. Таким образом, многочлен с действительными коэффициентами имеет разложение:
- 22. Пример: Решение. Действительных корней нет. Комплексные корни:
- 25. Точно также, Окончательно
Слайд 2
Лекция 4
2. Многочлены в комплексной области.
1. Комплексная функция действительного
аргумента.
Комплексные функции и многочлены.
Слайд 11В развернутом виде:
Такое уравнение называется алгебраическим уравнением n-ой степени.
Теорема Безу.
Слайд 15Основная теорема алгебры
Многочлен n-ой степени имеет ровно n
корней, если каждый корень считать столько раз, какова его кратность.
Слайд 16Таким образом:
Комплексные корни многочлена с действительными коэффициентами являются сопряженными парами корней
.
Слайд 17Из теоремы Безу и основной теоремы алгебры следует,
что всякий многочлен степени
n можно разложить на
множители:
множители:
Слайд 191.
Линейные множители
- соответствуют действительным корням zi кратности ki,
2.
Квадратичные множители
где p,q -
действительные числа,
- соответствуют парам комплексно-сопряжённых корней кратности kj