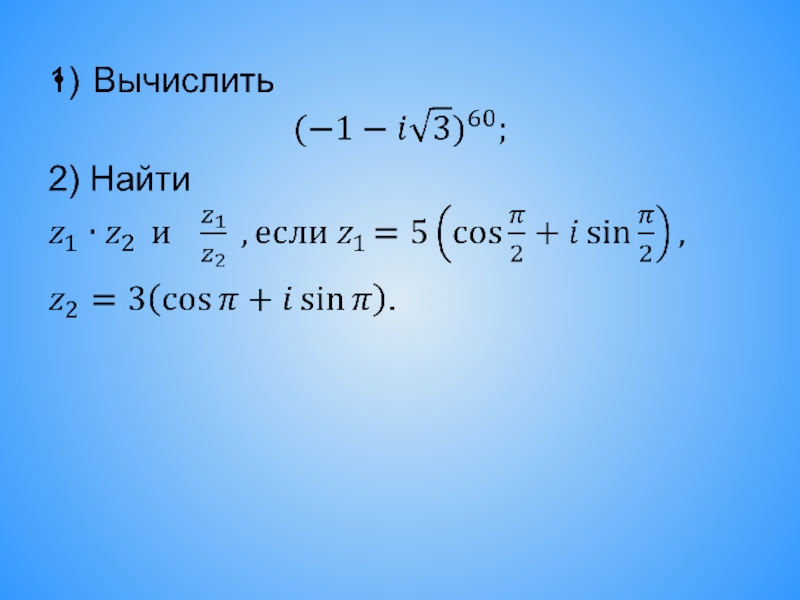- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Комплексные числа и действия над ними. (Лекция 1) презентация
Содержание
- 1. Комплексные числа и действия над ними. (Лекция 1)
- 2. ПЛАН 1. Основные понятия. 2.
- 3. 1. Основные понятия.
- 4.
- 5. 2. Геометрическое изображение комплексных чисел. М x y
- 6.
- 7. 3. Формы записи комплексных чисел.
- 8.
- 9.
- 10. 4. Действия над комплексными
- 11. Вычитание комплексныхчисел
- 12. Умножение комплексных чисел
- 13.
- 14. Деление комплексных чисел
- 15. Извлечение корней из комплексных чисел
- 16. Зачем изучать комплексные числа? На множестве С
- 17. Одним из важных приложений ТФКП является
- 18.
- 19.
- 20.
- 21.
Слайд 2
ПЛАН
1. Основные понятия.
2. Геометрическое изображение комплексных чисел.
3. Формы записи комплексных чисел.
4.
Действия над комплексными числами.
5. Зачем изучать комплексные числа?
5. Зачем изучать комплексные числа?
Слайд 16Зачем изучать комплексные числа?
На множестве С вводятся понятия функции, предела таким
образом, что соответствующие понятия действительного анализа рассматриваются как частный случай. При этом сохраняются известные свойства функций действительного переменного: теоремы о пределах, правила дифференцирования, формулы интегрирования и т.д. Однако, благодаря расширению класса функций появляются новые свойства. Например, доказывается, что из существования производной функции следует существование её производных n-го порядка в области. Устанавливается, что все элементарные функции связаны между собой: тригонометрические функции выражаются через показательную функцию, а обратные тригонометрические функции – через логарифмическую. Значительно глубже, чем в анализе функций действительного переменного, развита геометрическая теория – конформные отображения. Благодаря сочетанию аналитических и геометрических методов теория функций комплексного переменного находит широкое применение в других разделах математики и прикладных задач.
Слайд 17
Одним из важных приложений ТФКП является операционное исчисление, которое применяется для
решения обыкновенных дифференциальных уравнений и разностных уравнений с постоянными коэффициентами.