- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Комплексные числа презентация
Содержание
- 1. Комплексные числа
- 2. 22.1. АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ
- 3. Число х называется действительной частью числа z:
- 4. Действительное число х является частным случаем комплексного
- 5. Комплексные числа называются сопряженными Комплексные
- 6. Арифметические действия над множеством комплексныx чисел 1 Сумма (разность) комплексных чисел:
- 7. 2 Произведение комплексных чисел:
- 8. Поскольку Например:
- 9. 3 Деление комплексных чисел:
- 10. Поскольку
- 11. Пример. Найти сумму, разность, произведение и частное комплексных чисел:
- 12. Решение
- 13. Если для изображения действительных чисел используются точки
- 14. По оси абсцисс откладывается действительная часть комплексного
Слайд 222.1. АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ
НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ
Комплексным числом называется выражение вида
где х
i – мнимая единица:
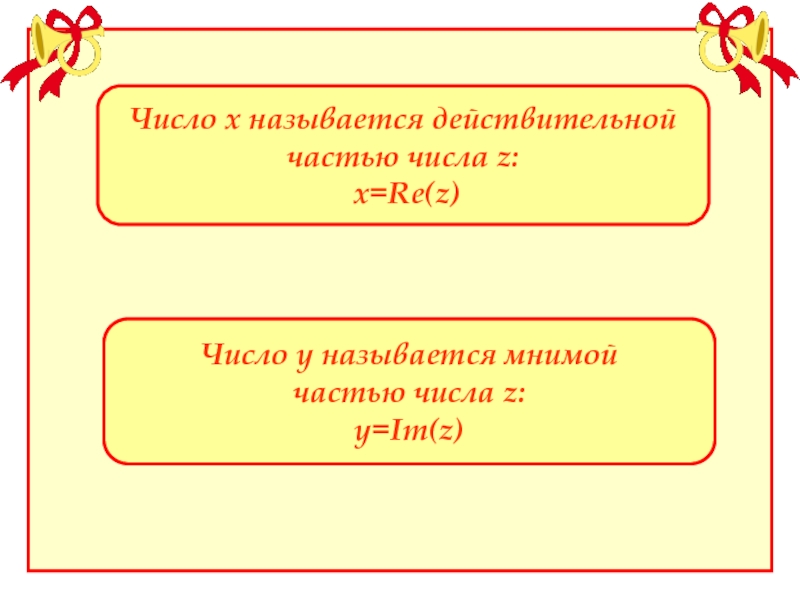
Слайд 3Число х называется действительной
частью числа z:
х=Re(z)
Число у называется мнимой
частью
у=Im(z)
Слайд 4Действительное число х является частным случаем комплексного числа
при у=0.
Комплексные числа
не являющиеся действительными, т.е. при
называются мнимыми, а при
называются чисто мнимыми.
Слайд 5
Комплексные числа
называются сопряженными
Комплексные числа
называются равными, если равны их действительные и мнимые
Слайд 13Если для изображения действительных чисел используются точки числовой прямой, то для
Плоскость называется комплексной, если любому комплексному числу
ставятся в соответствие точки плоскости ХОУ, причем это соответствие взаимно однозначное.
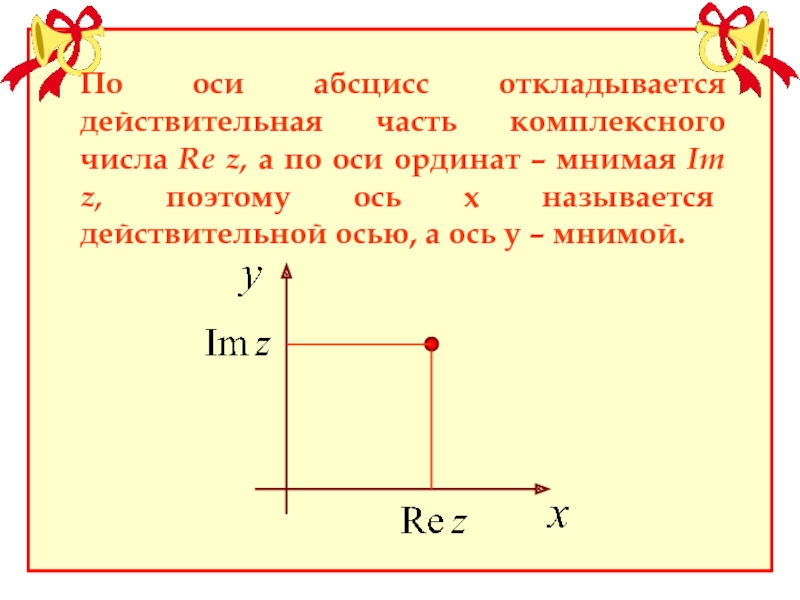
Слайд 14По оси абсцисс откладывается действительная часть комплексного числа Re z, а