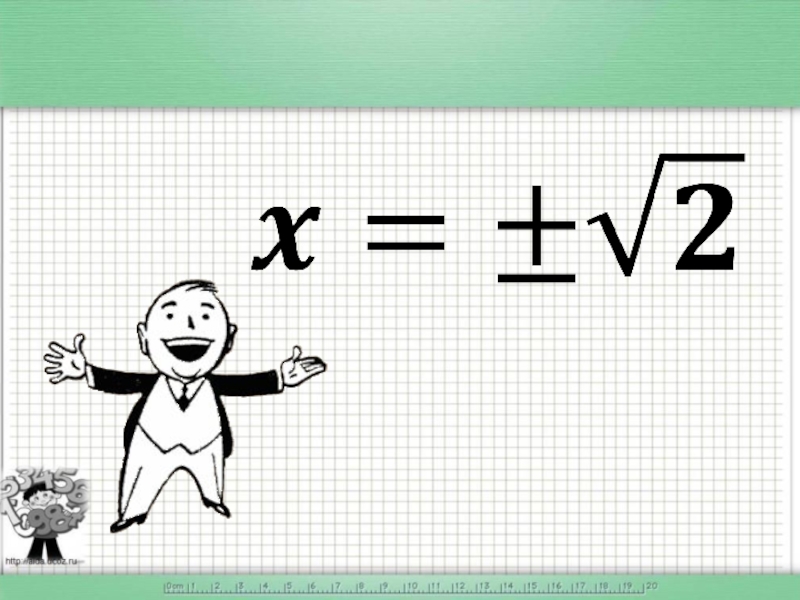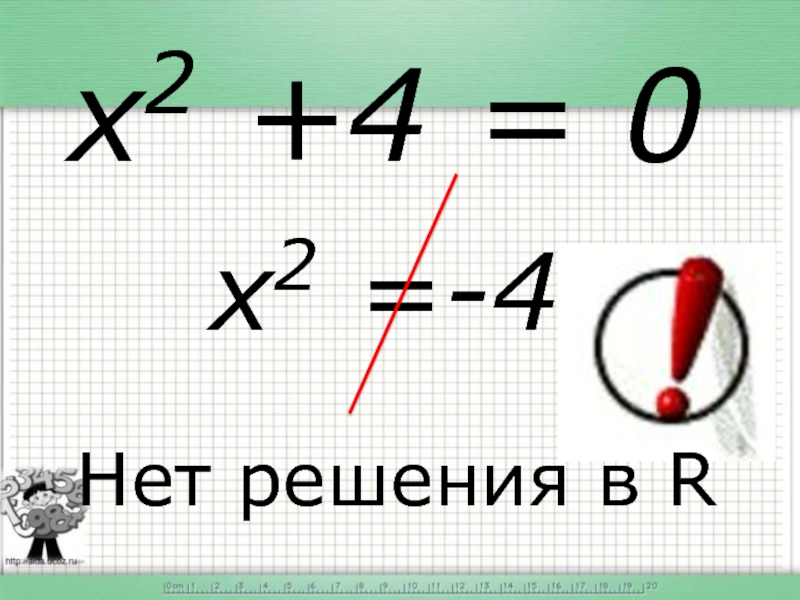- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Комплексные числа презентация
Содержание
- 1. Комплексные числа
- 2. Числа не управляют миром, но показывают, как управляется мир И. Гёте
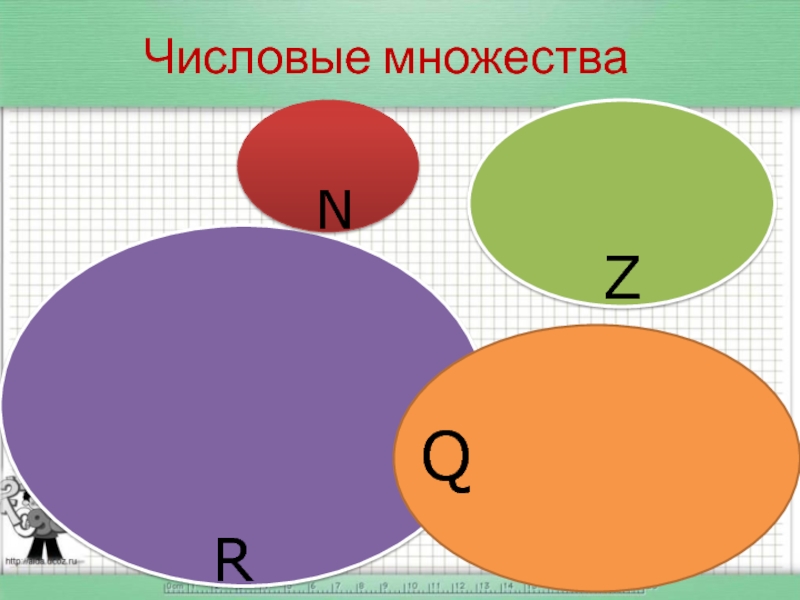
- 3. Числовые множества
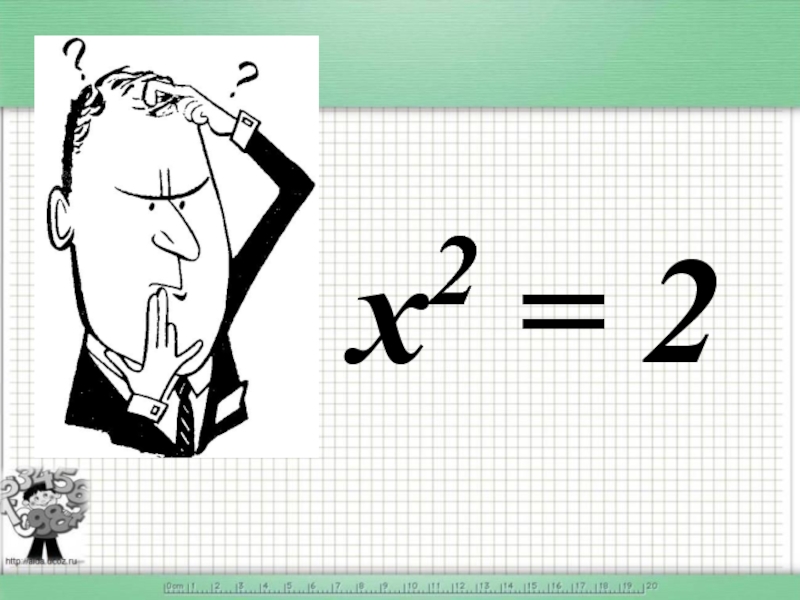
- 4. x2 = 2
- 5.
- 6. x2 +4 = 0 Нет решения в R
- 7. Решите уравнения: Вариант I Вариант II
- 8. x2 = -1 i – мнимая единица i2 = -1
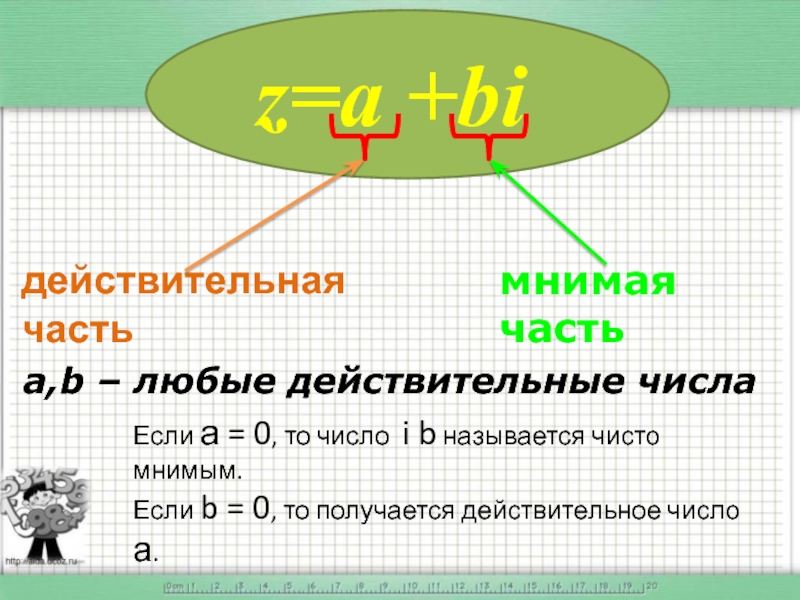
- 9. a,b – любые действительные числа Если а
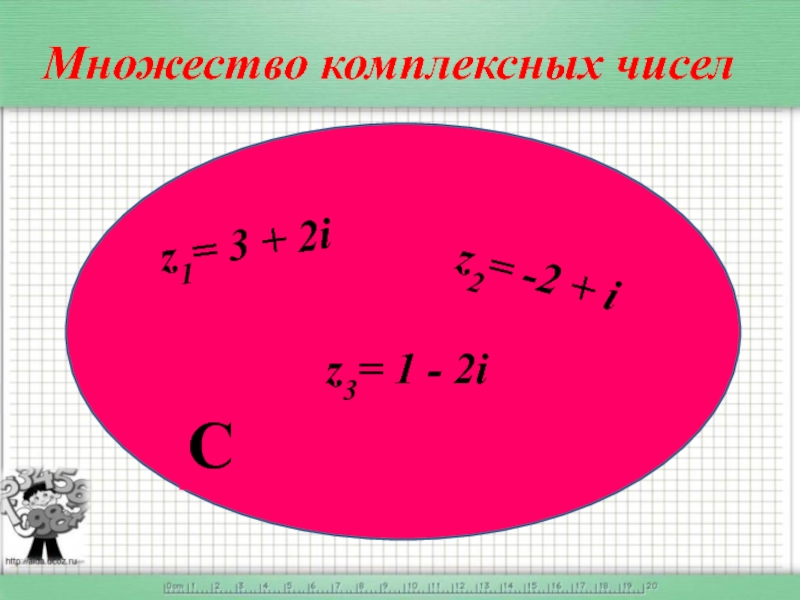
- 10. Множество комплексных чисел
- 11. Геометрическое изображение комплексных чисел. Рассмотрим плоскость с
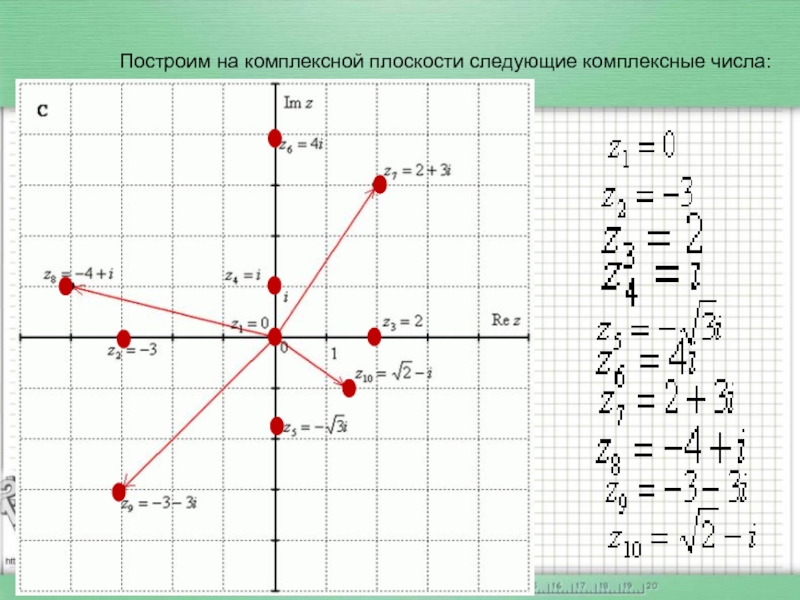
- 12. Построим на комплексной плоскости следующие комплексные числа:
- 13. Геометрическое изображение комплексных чисел. модуль аргумент Z = a+bi
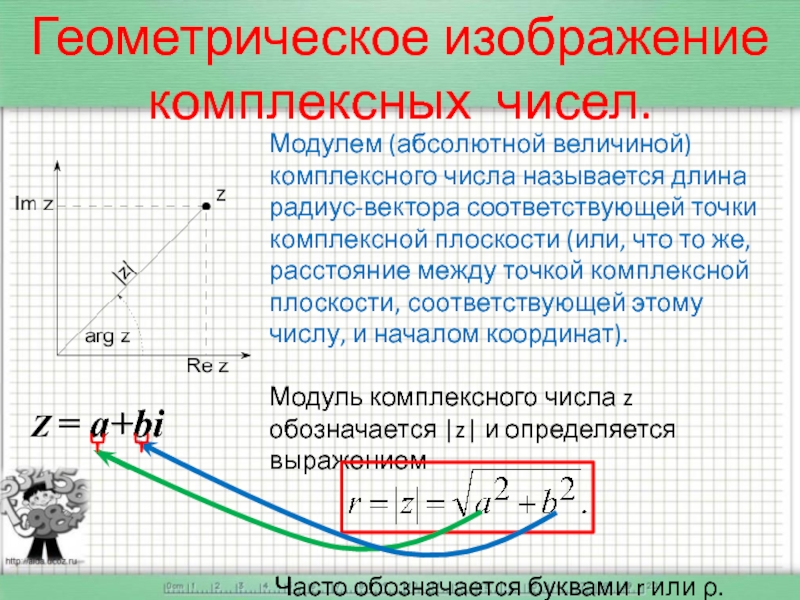
- 14. Модулем (абсолютной величиной) комплексного числа называется длина
- 15. СУММА z1 = a1 + b1i z2
- 16. а)Z1 =5+4i
- 17. РАЗНОСТЬ Z1 = a1+b1i Z2 = a2+b2i
- 18. РАЗНОСТЬ z1 = a1 + b1i z2
- 19. а)Z1 =5+4i
- 20. Возведение в степень
- 21. Самостоятельная работа Для комплексных чисел z1 и
- 22. Произведение Произведением комплексных чисел является комплексное число:
- 23. Если у комплексного числа сохранить действительную часть
- 24. Деление Для того, чтобы разделить два
Слайд 7Решите уравнения:
Вариант I
Вариант II
Решения нет
во множестве действительных чисел!!!!!
x2 +1 = 0
x2 +9 = 0
Слайд 9a,b – любые действительные числа
Если а = 0, то число i
Если b = 0, то получается действительное число а.
Слайд 11Геометрическое изображение комплексных чисел.
Рассмотрим плоскость с прямоугольной системой
координат. Каждому комплексному
Такая плоскость называется комплексной.
Действительная часть числа на ней занимает
горизонтальную ось, мнимая часть изображается на вертикальной оси; по этой причине горизонтальная и вертикальная оси
называются соответственно вещественной и
мнимой осями.
Вещественная ось
Мнимая ось
Слайд 14Модулем (абсолютной величиной) комплексного числа называется длина радиус-вектора соответствующей точки комплексной
Модуль комплексного числа z обозначается |z| и определяется выражением
Часто обозначается буквами r или ρ.
Геометрическое изображение комплексных чисел.
Z = a+bi
Слайд 21Самостоятельная работа
Для комплексных чисел z1 и z2 найдите их сумму z1
z1 = 1+i, z2 = -1+2i;
Ответ:
Слайд 23Если у комплексного числа сохранить действительную часть и поменять знак у
комплексное число;
сопряженное число.
Сопряженные числа