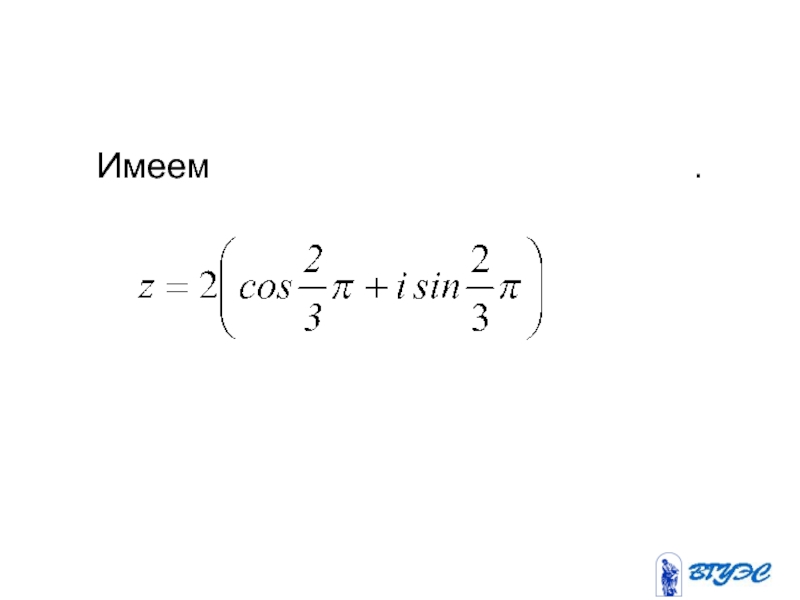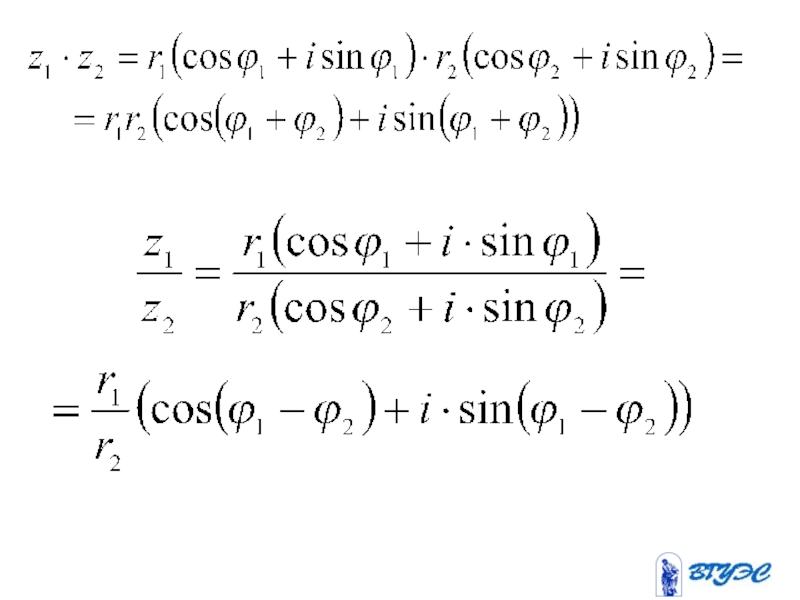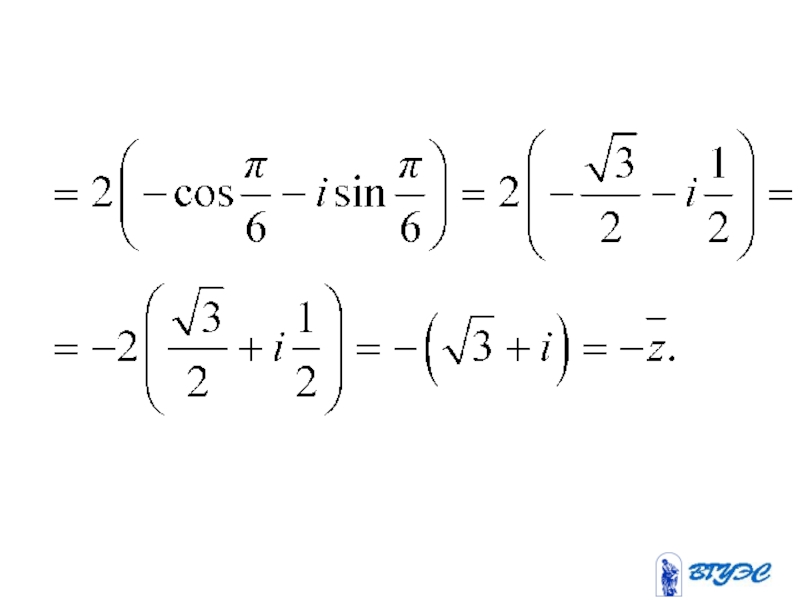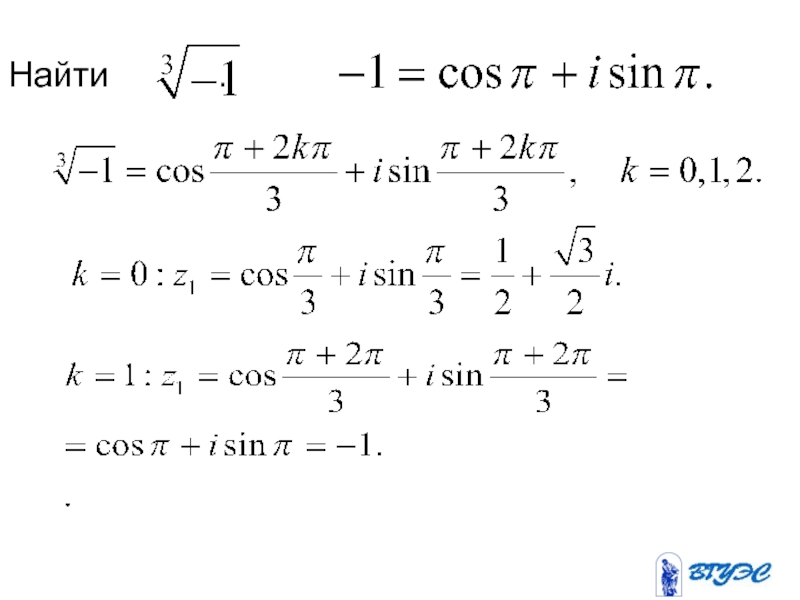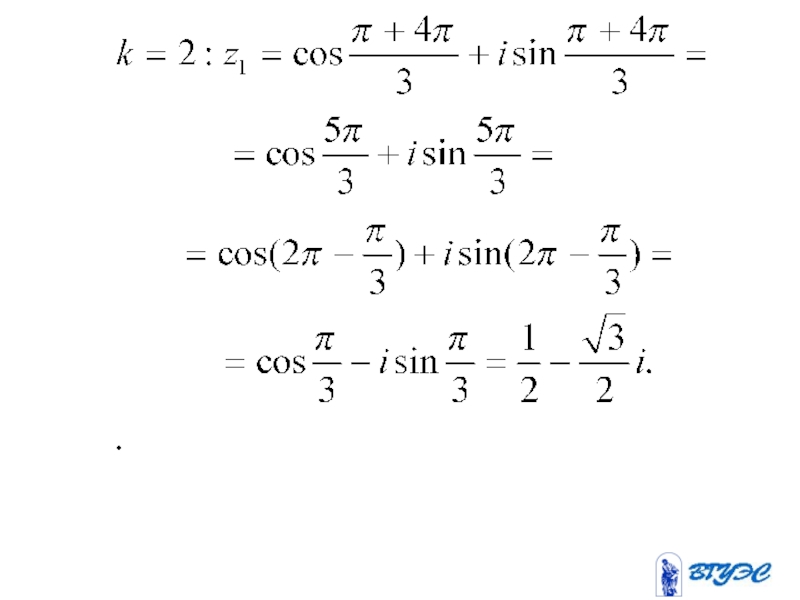- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Комплексные числа презентация
Содержание
- 1. Комплексные числа
- 2. Комплексным числом называется
- 3. называется алгебраической формой
- 4. Число x называется действительной частью, y–мнимой
- 5. Если
- 6. Два комплексных числа
- 7. Всякое комплексное число
- 8. Число z=0 ставится в соответствие
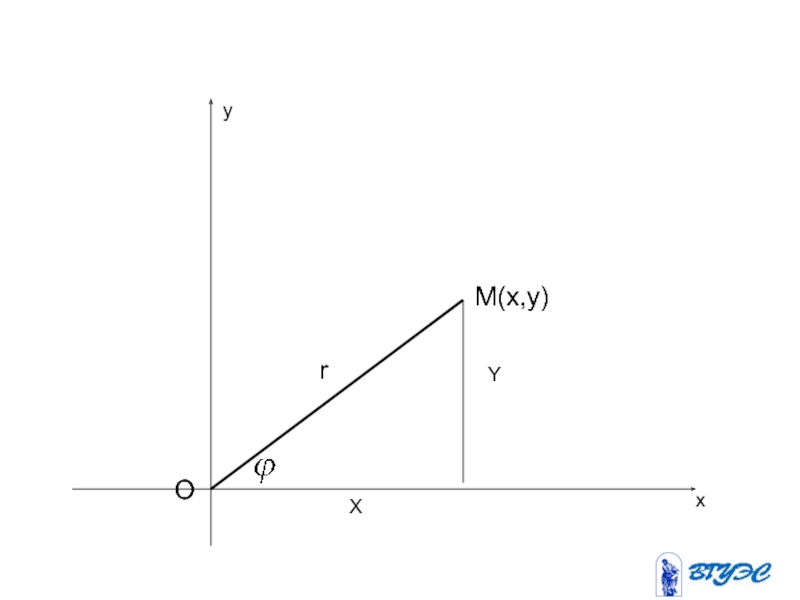
- 9. O M(x,y) X Y r х у
- 10. Модуль комплексного числа
- 11. Тригонометрическая и показательная формы комплексного числа
- 12. , Положительным направлением изменения угла
- 13. ,
- 14. Записать в тригонометрической форме комплексное
- 15. Имеем
- 16. Показательная форма комплексного числа Используя
- 17. Действия над комплексными числами
- 18. Действия над комплексными числами
- 19. Действия над комплексными числами
- 20. Действия над комплексными
- 22. Формула Муавра
- 23. Извлечение корня В тригонометрической
- 24. Аргумент комплексного числа. Аргумент комплексного
- 25. Пример . Возвести число
- 26. Тогда по формуле Муавра получим
- 28. Найти .
Комплексным числом называется число вида где , а x
Слайд 3называется алгебраической формой
записи комплексного
числа.
Выражение
называется алгебраической формой
записи комплексного числа.
Слайд 4Число x называется действительной частью,
y–мнимой частью комплексного числа z.
Это
записывают следующим образом:
Слайд 5 Если , то
число называют
чисто мнимым.
Если , то получается
вещественное число.
Два комплексных числа
и
называются сопряженными.
чисто мнимым.
Если , то получается
вещественное число.
Два комплексных числа
и
называются сопряженными.
Слайд 6 Два комплексных числа
и
равны друг другу, если
и .
Комплексное число z считается
равным нулю, если x=y=0.
равны друг другу, если
и .
Комплексное число z считается
равным нулю, если x=y=0.
Слайд 7 Всякое комплексное число можно
изобразить
точкой на плоскости, т.к. каждому z соответствует
упорядоченная пара вещественных
чисел (x;y).
упорядоченная пара вещественных
чисел (x;y).
Слайд 8
Число z=0 ставится в соответствие началу координатной плоскости. Такую плоскость
мы в дальнейшем будем называть комплексной плоскостью, ось абсцисс–действительной, а ось ординат– мнимой осью комплексной плоскости.
Слайд 11 Тригонометрическая и показательная формы комплексного числа
Для определения
положения точки на плоскости можно пользоваться полярными координатами , где r–расстояние точки от начала координат, а φ–угол, который составляет радиус–вектор этой точки с положительным направлением оси Ox.
Слайд 12,
Положительным направлением изменения угла φ считается направление против часовой
стрелки. Воспользовавшись связью декартовых и полярных координат:
, ,
получим тригонометрическую форму записи комплексного числа
, ,
получим тригонометрическую форму записи комплексного числа
,
Слайд 13,
, где
,
φ–аргумент комплексного числа, который находят из формул
,
или в силу того, что ,
,
φ–аргумент комплексного числа, который находят из формул
,
или в силу того, что ,
,
Слайд 14 Записать в тригонометрической форме комплексное число
.
Очевидно точка
находится во 2-й четверти и поэтому
Очевидно точка
находится во 2-й четверти и поэтому
Пример
.
.
Слайд 16Показательная форма комплексного числа
Используя формулу Эйлера
,
получаем показательную форму записи комплексного числа
получаем показательную форму записи комплексного числа
Слайд 23Извлечение корня
В тригонометрической форме корень n–й степени вычисляют
по формуле:
,
, а в показательной–по формуле .
,
, а в показательной–по формуле .
Слайд 24Аргумент комплексного числа.
Аргумент комплексного числа можно брать с точностью
до . Это значит, что аргументы сопряженных чисел отличаются знаком. Так, например, аргументом числа можно считать значения
или .
или .
