- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Каскады из правильных многогранников презентация
Содержание
- 1. Каскады из правильных многогранников
- 2. Куб и тетраэдр Тетраэдр можно вписать в
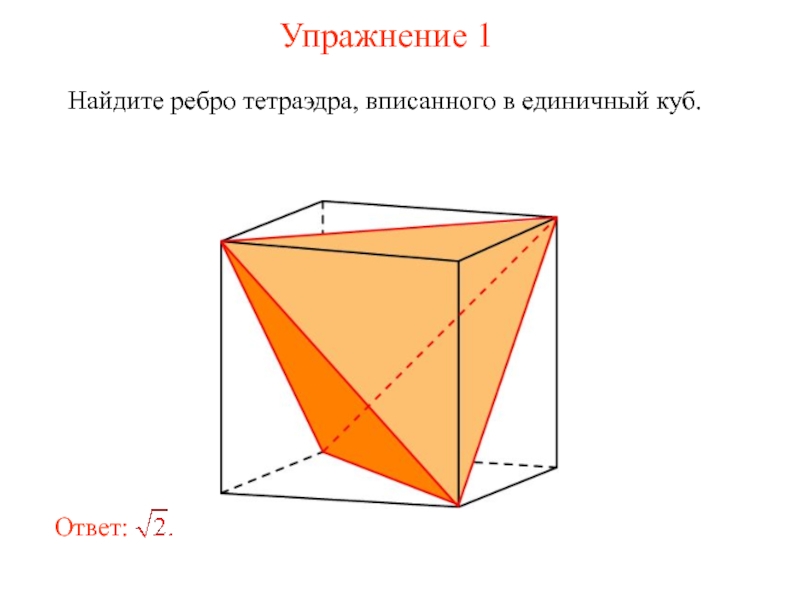
- 3. Упражнение 1 Найдите ребро тетраэдра, вписанного в единичный куб.
- 4. Куб и октаэдр В куб можно вписать
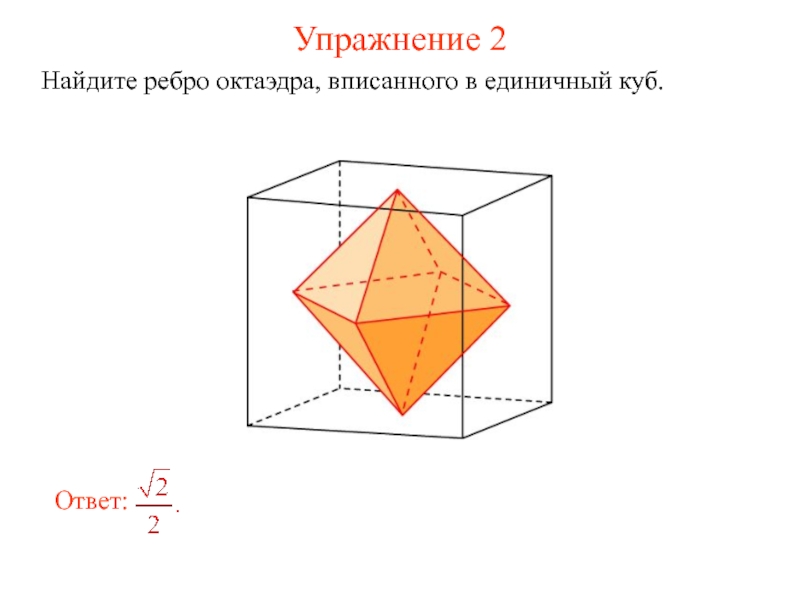
- 5. Упражнение 2 Найдите ребро октаэдра, вписанного в единичный куб.
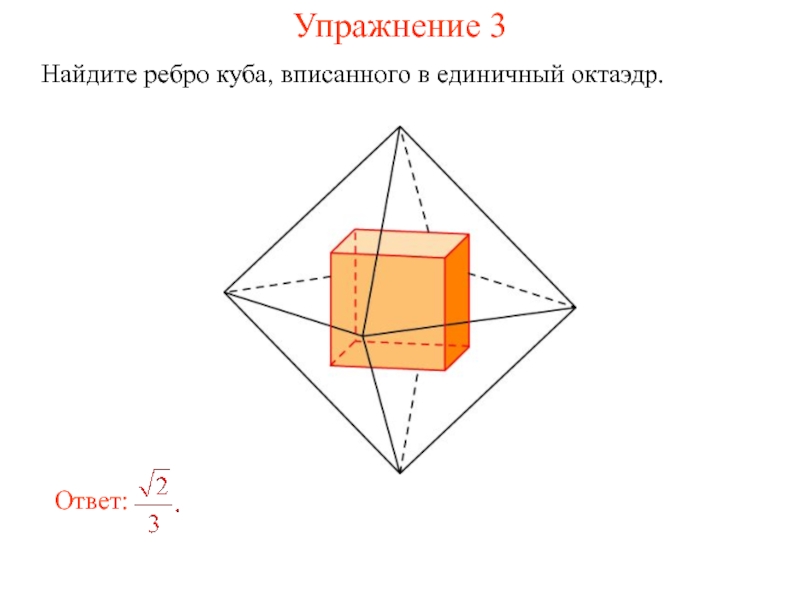
- 6. Упражнение 3 Найдите ребро куба, вписанного в единичный октаэдр.
- 7. Куб и икосаэдр
- 8. Упражнение 4 Впишем в куб икосаэдр. Для
- 9. Куб и додекаэдр
- 10. Упражнение 5 Впишем в куб додекаэдр. Для
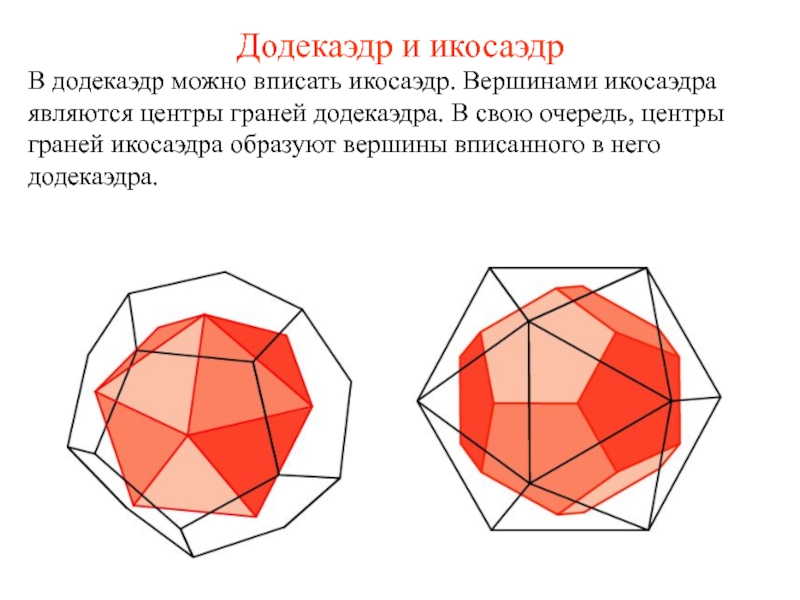
- 11. Додекаэдр и икосаэдр В додекаэдр можно вписать
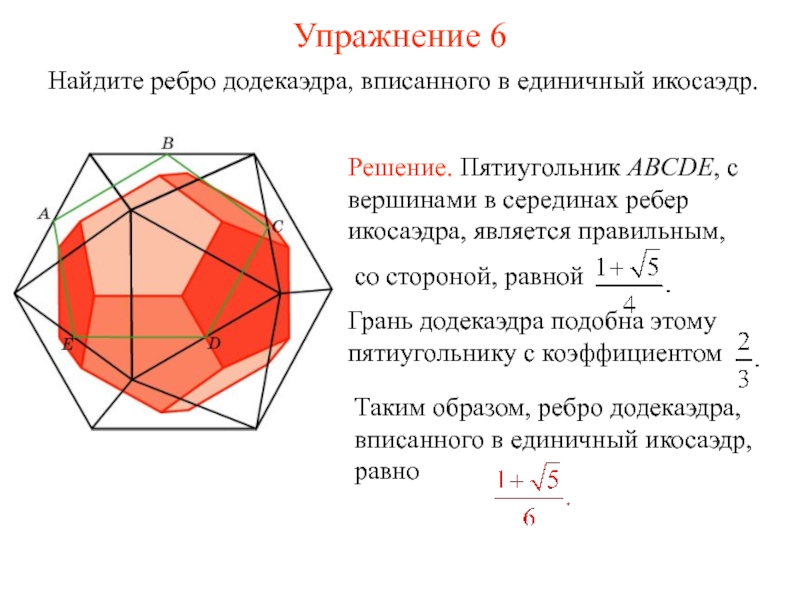
- 12. Упражнение 6 Найдите ребро додекаэдра, вписанного в единичный икосаэдр.
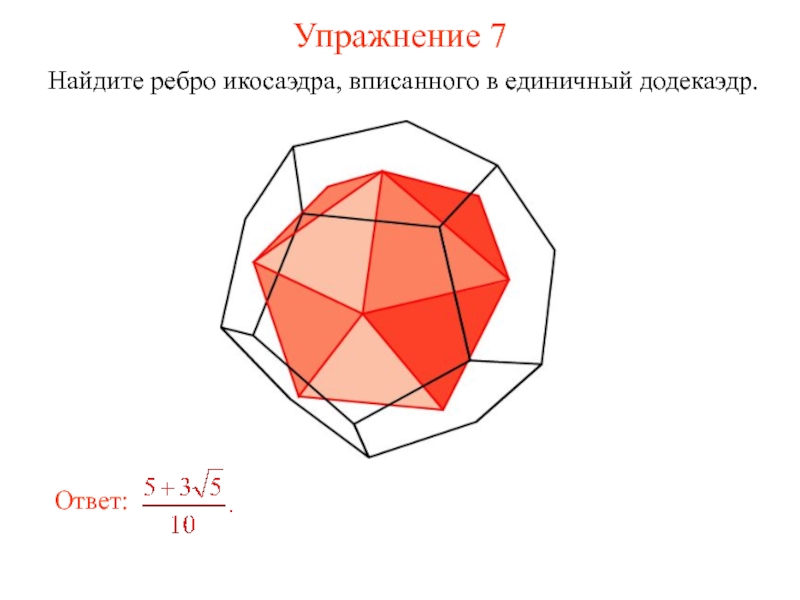
- 13. Упражнение 7 Найдите ребро икосаэдра, вписанного в единичный додекаэдр.
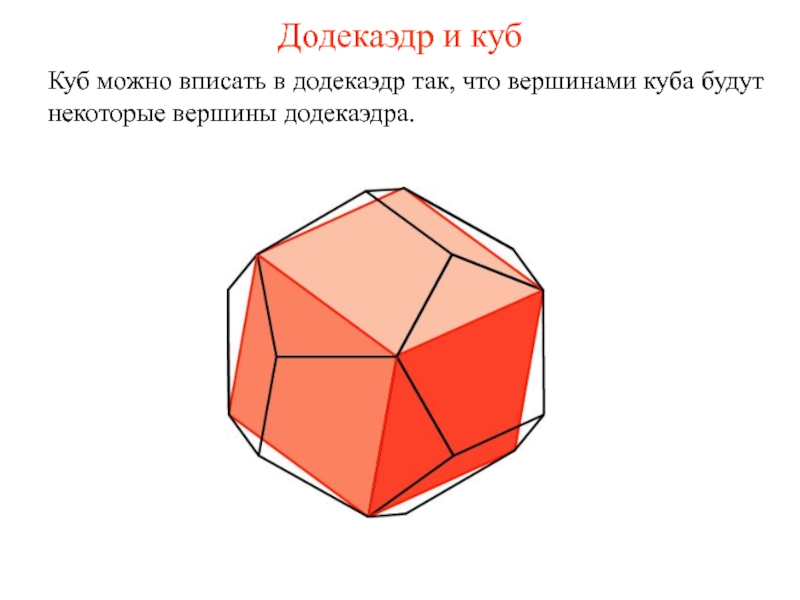
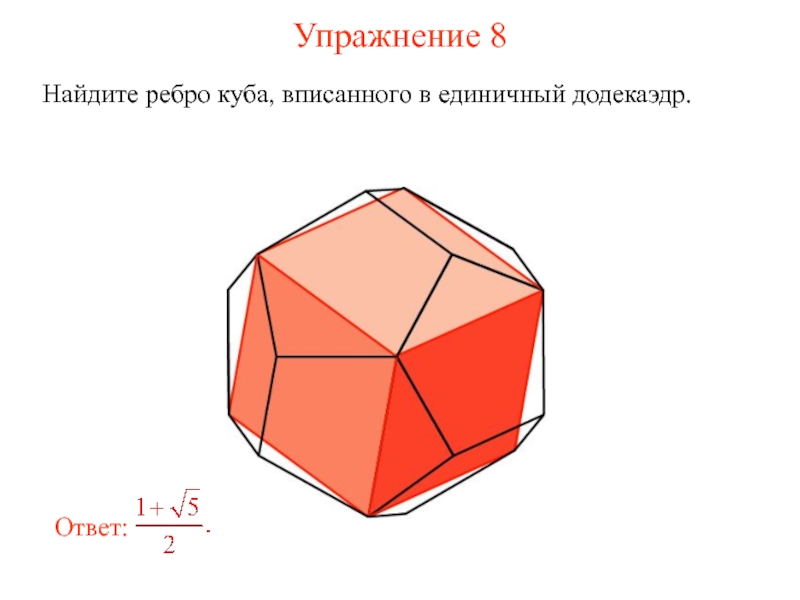
- 14. Додекаэдр и куб Куб можно вписать в
- 15. Упражнение 8 Найдите ребро куба, вписанного в единичный додекаэдр.
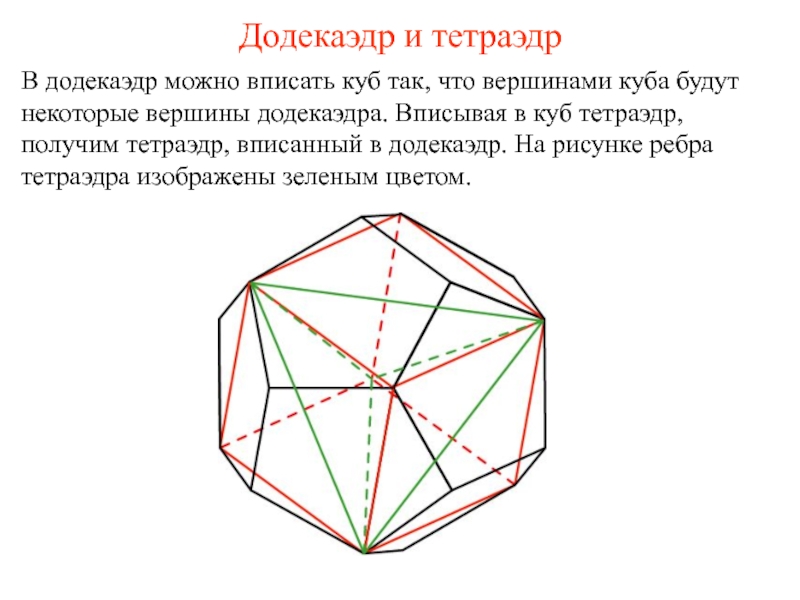
- 16. Додекаэдр и тетраэдр В додекаэдр можно вписать
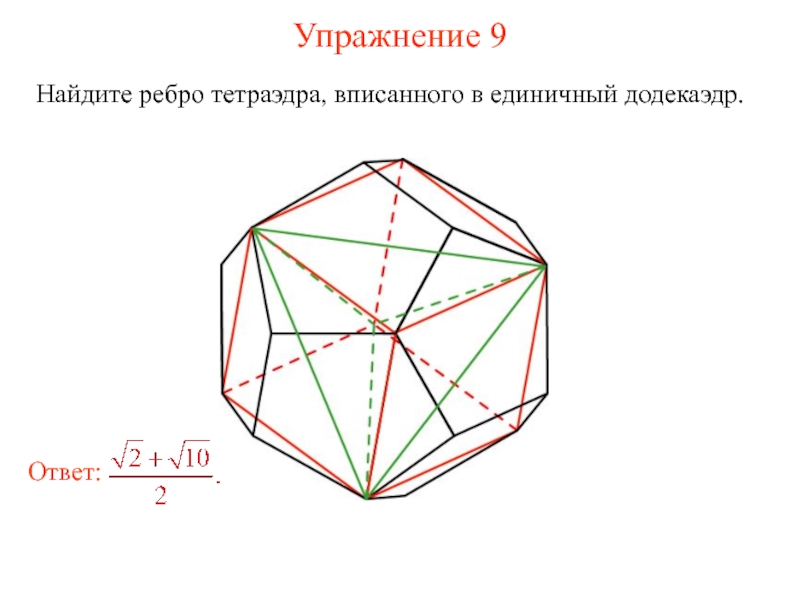
- 17. Упражнение 9 Найдите ребро тетраэдра, вписанного в единичный додекаэдр.
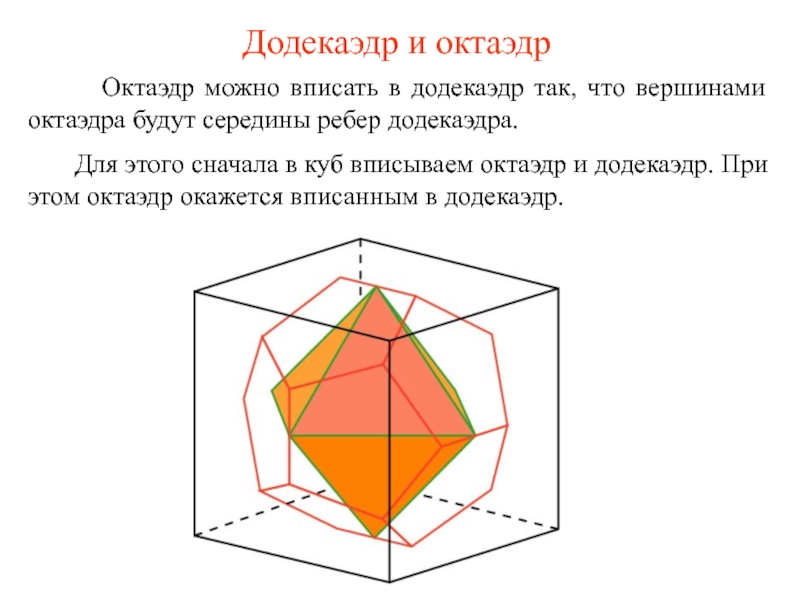
- 18. Додекаэдр и октаэдр
- 19. Упражнение 10 Найдите ребро октаэдра, вписанного в единичный додекаэдр.
- 20. Икосаэдр и куб В икосаэдр можно вписать
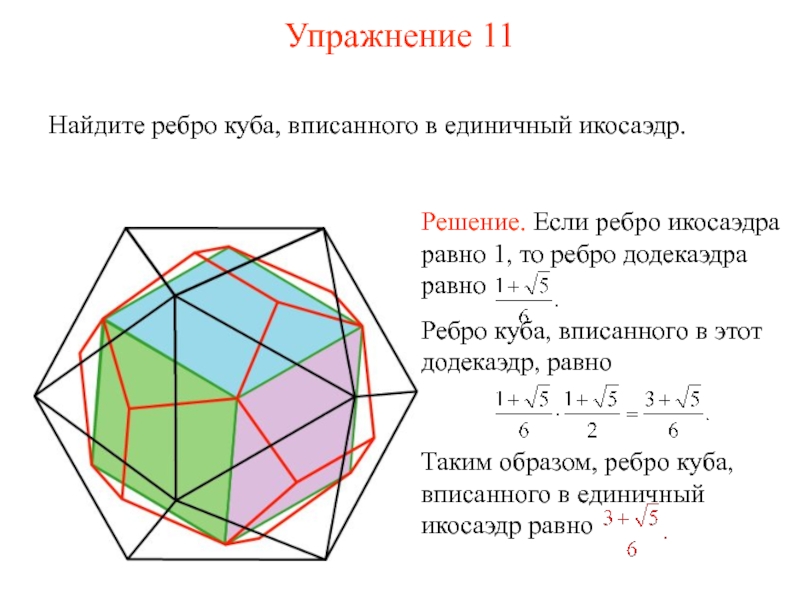
- 21. Упражнение 11 Найдите ребро куба, вписанного в единичный икосаэдр.
- 22. Икосаэдр и тетраэдр В икосаэдр можно вписать
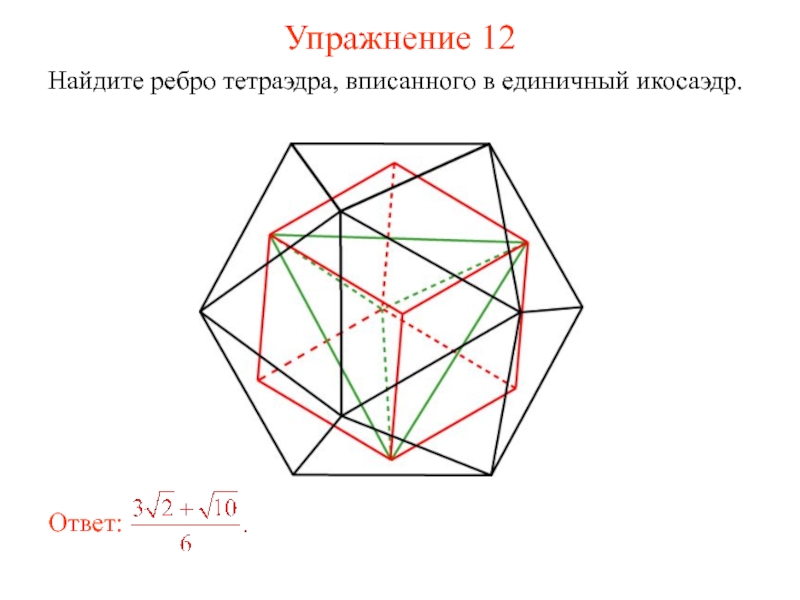
- 23. Упражнение 12 Найдите ребро тетраэдра, вписанного в единичный икосаэдр. Ответ:
- 24. Икосаэдр и октаэдр
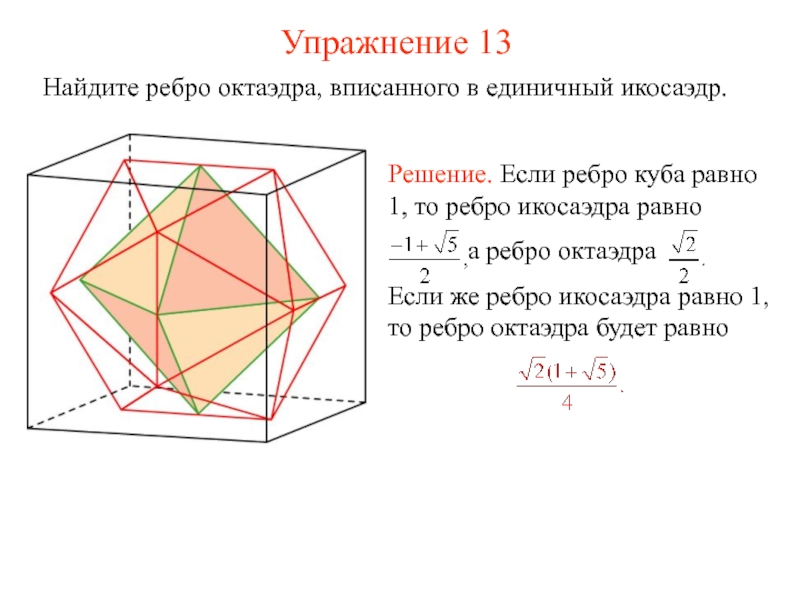
- 25. Упражнение 13 Найдите ребро октаэдра, вписанного в единичный икосаэдр.
- 26. Октаэдр и тетраэдр В октаэдр можно вписать
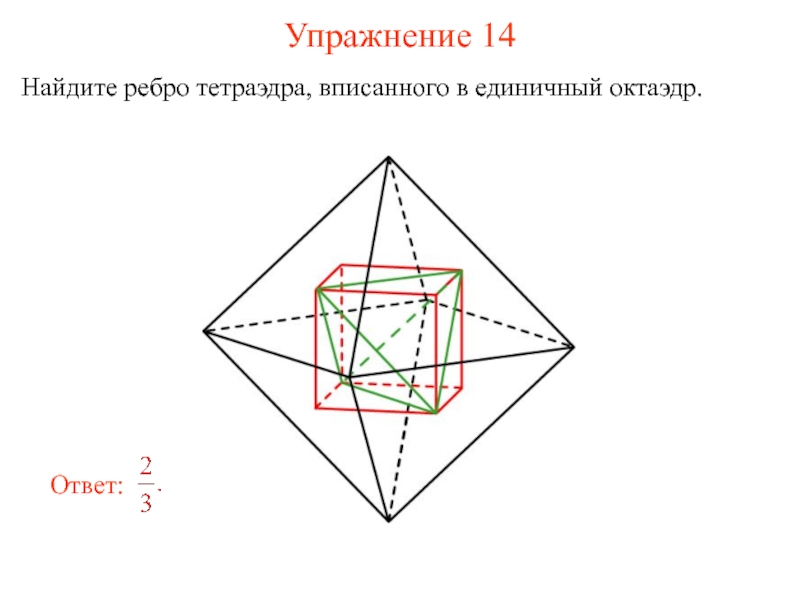
- 27. Упражнение 14 Найдите ребро тетраэдра, вписанного в единичный октаэдр.
- 28. Октаэдр и икосаэдр
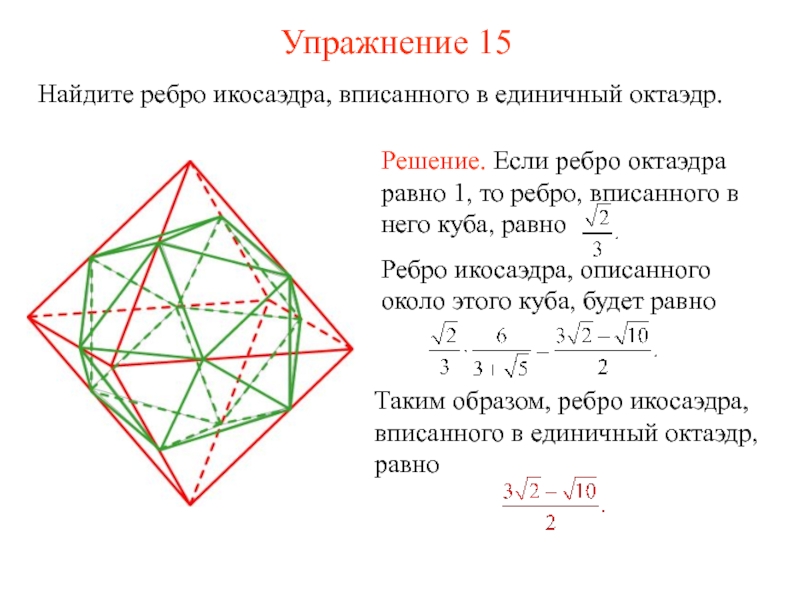
- 29. Упражнение 15 Найдите ребро икосаэдра, вписанного в единичный октаэдр.
- 30. Октаэдр и додекаэдр
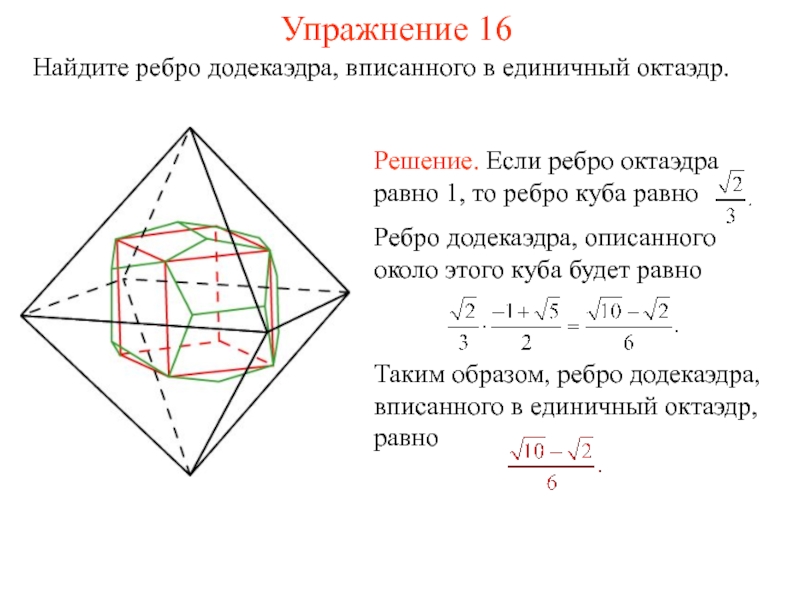
- 31. Упражнение 16 Найдите ребро додекаэдра, вписанного в единичный октаэдр.
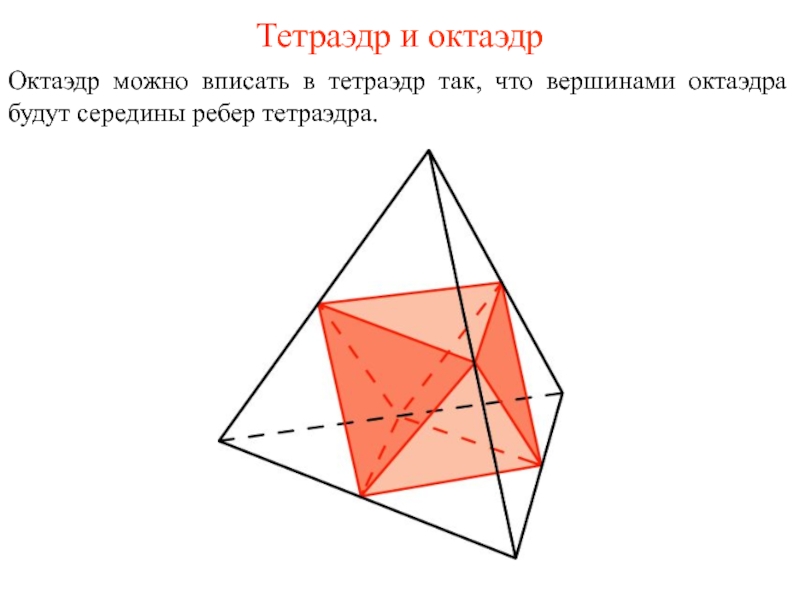
- 32. Тетраэдр и октаэдр Октаэдр можно вписать в
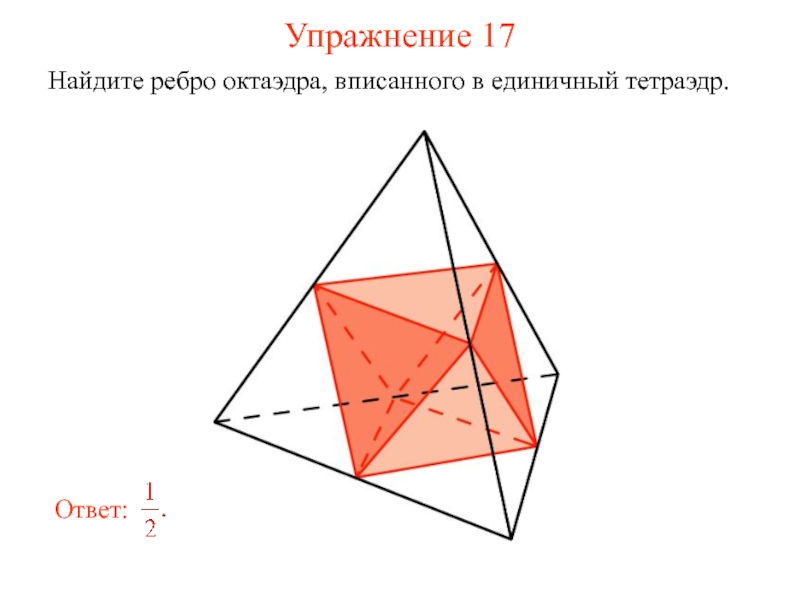
- 33. Упражнение 17 Найдите ребро октаэдра, вписанного в единичный тетраэдр.
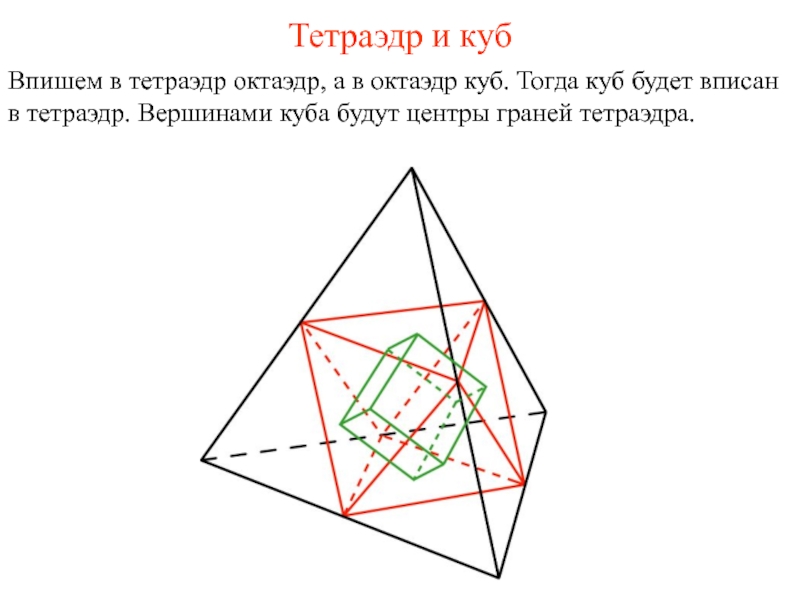
- 34. Тетраэдр и куб Впишем в тетраэдр октаэдр,
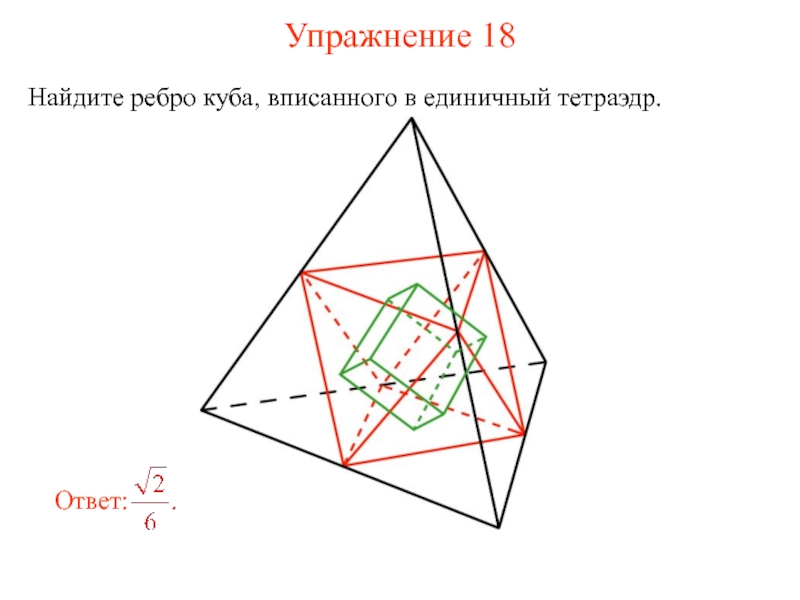
- 35. Упражнение 18 Найдите ребро куба, вписанного в единичный тетраэдр.
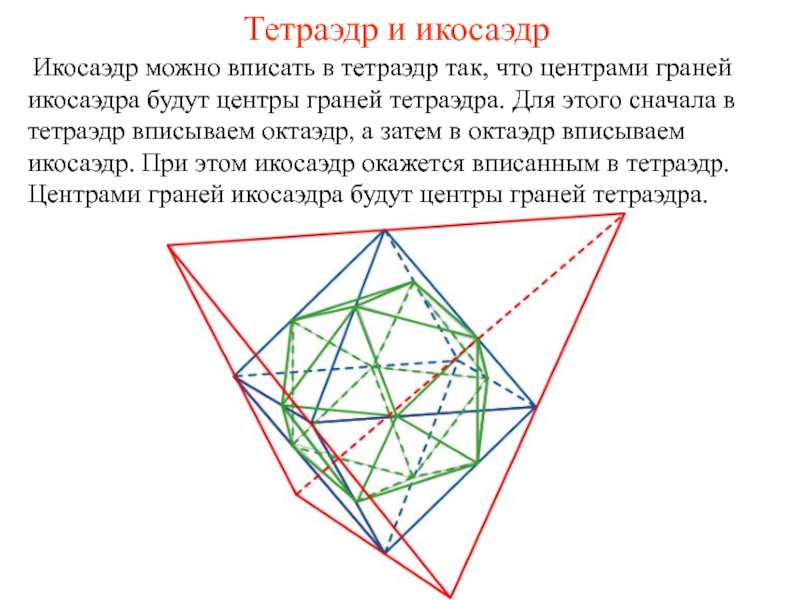
- 36. Тетраэдр и икосаэдр Икосаэдр можно вписать
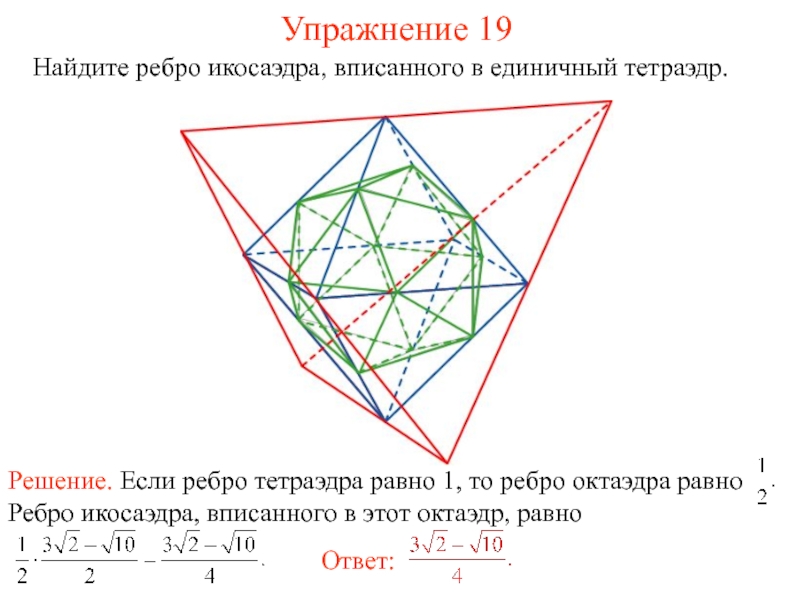
- 37. Упражнение 19 Найдите ребро икосаэдра, вписанного в единичный тетраэдр.
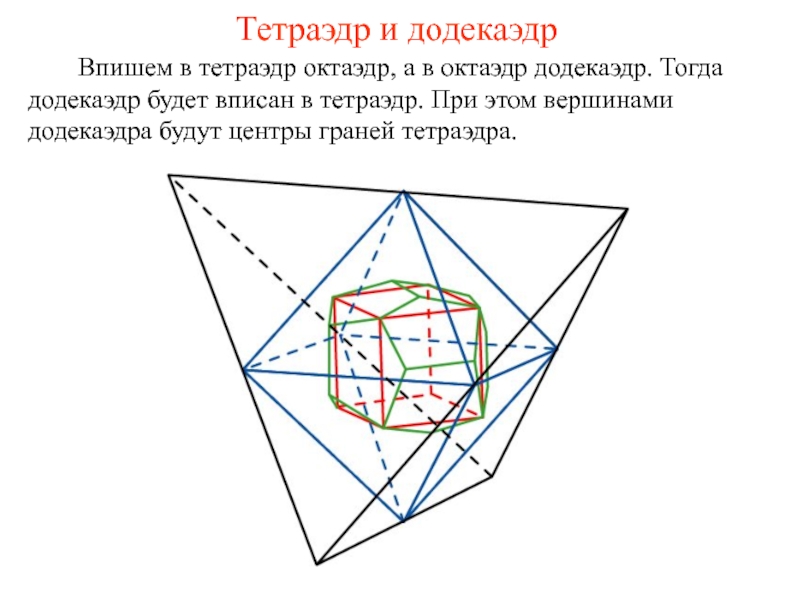
- 38. Тетраэдр и додекаэдр
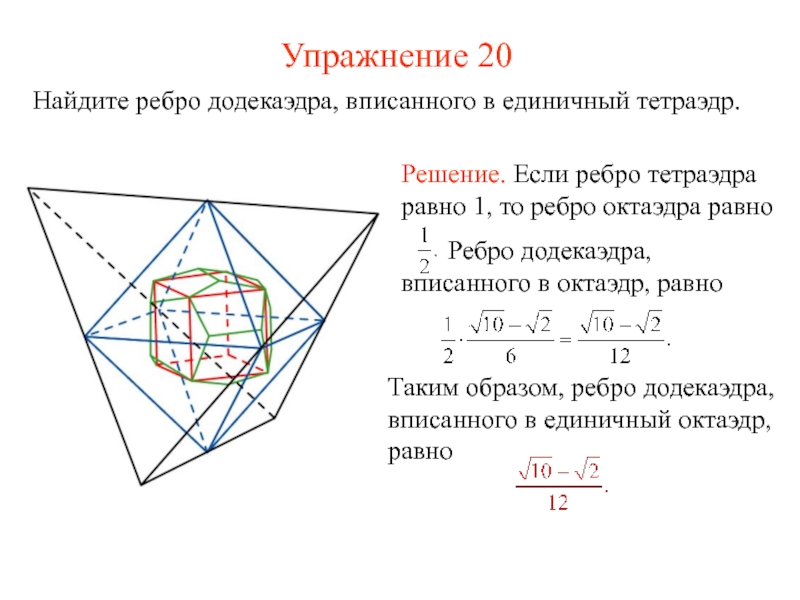
- 39. Упражнение 20 Найдите ребро додекаэдра, вписанного в единичный тетраэдр.
- 40. 120 каскадов В качестве первого можно взять
Слайд 1Каскады из правильных многогранников
Правильные многогранники можно вписывать друг в друга.
При
Вершинами вписанного многогранника являются некоторые вершины описанного многогранника.
Вершинами вписанного многогранника являются середины ребер описанного многогранника.
Вершинами вписанного многогранника являются центры граней описанного многогранника.
Серединами ребер вписанного многогранника являются центры граней описанного многогранника.
Центрами граней вписанного многогранника являются некоторые центры граней описанного многогранника.
Последовательное вписывание друг в друга правильных многогранников называется каскадом.
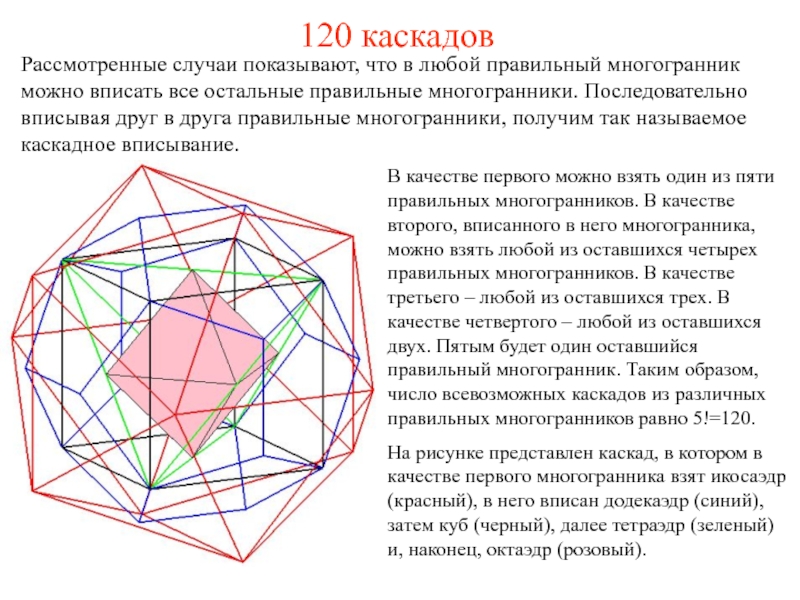
Здесь мы рассмотрим возможные варианты вписанности правильных многогранников и покажем, что имеется 5! = 120 каскадов.
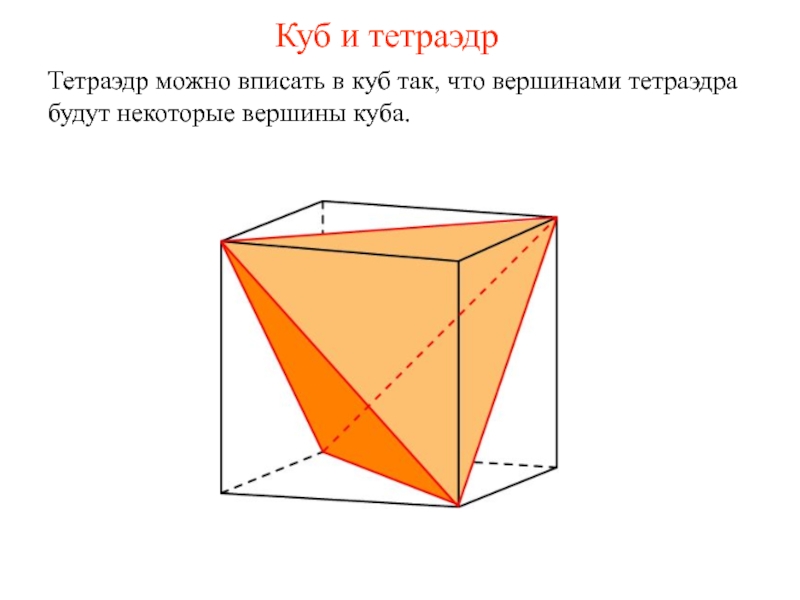
Слайд 2Куб и тетраэдр
Тетраэдр можно вписать в куб так, что вершинами тетраэдра
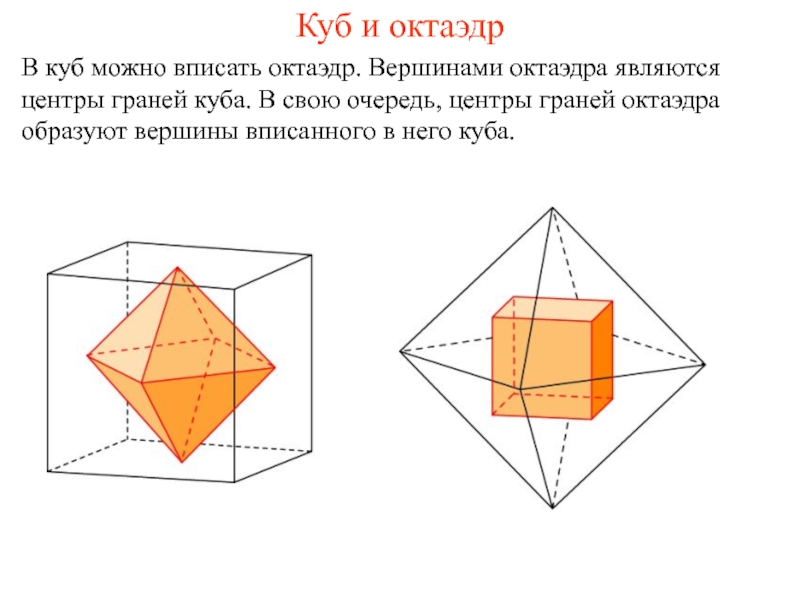
Слайд 4Куб и октаэдр
В куб можно вписать октаэдр. Вершинами октаэдра являются центры
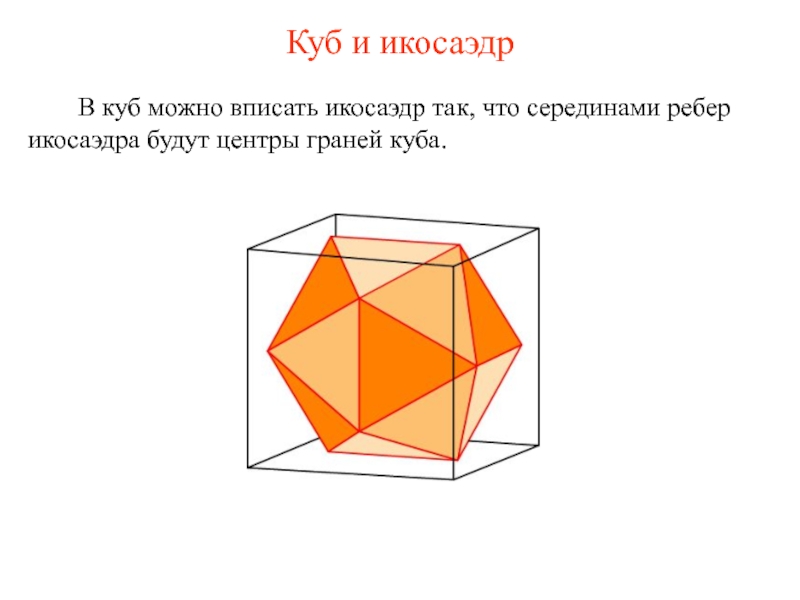
Слайд 7Куб и икосаэдр
В куб можно вписать
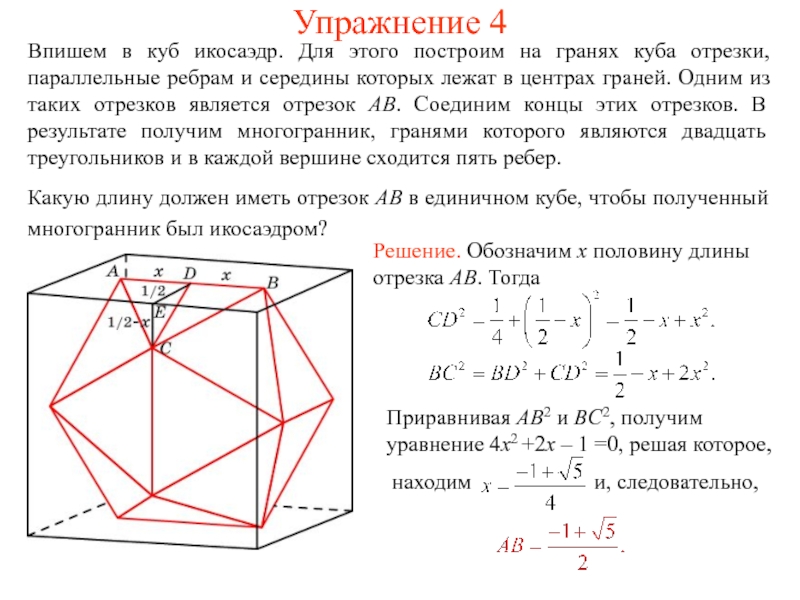
Слайд 8Упражнение 4
Впишем в куб икосаэдр. Для этого построим на гранях куба
Какую длину должен иметь отрезок AB в единичном кубе, чтобы полученный многогранник был икосаэдром?
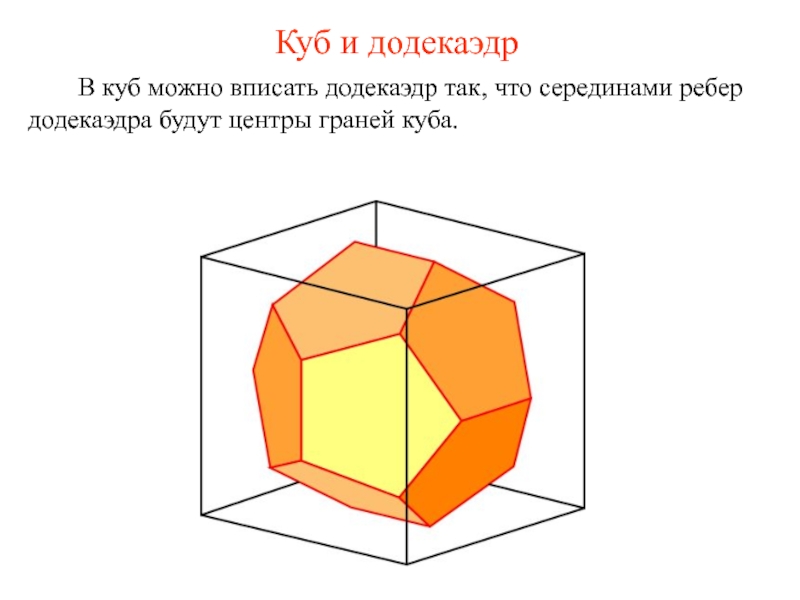
Слайд 9Куб и додекаэдр
В куб можно вписать
Слайд 10Упражнение 5
Впишем в куб додекаэдр. Для этого построим на гранях куба
Какую длину должен иметь отрезок AB в единичном кубе, чтобы полученный многогранник был додекаэдром?
Слайд 11Додекаэдр и икосаэдр
В додекаэдр можно вписать икосаэдр. Вершинами икосаэдра являются центры
Слайд 14Додекаэдр и куб
Куб можно вписать в додекаэдр так, что вершинами куба
Слайд 16Додекаэдр и тетраэдр
В додекаэдр можно вписать куб так, что вершинами куба
Слайд 18Додекаэдр и октаэдр
Октаэдр можно вписать в
Для этого сначала в куб вписываем октаэдр и додекаэдр. При этом октаэдр окажется вписанным в додекаэдр.
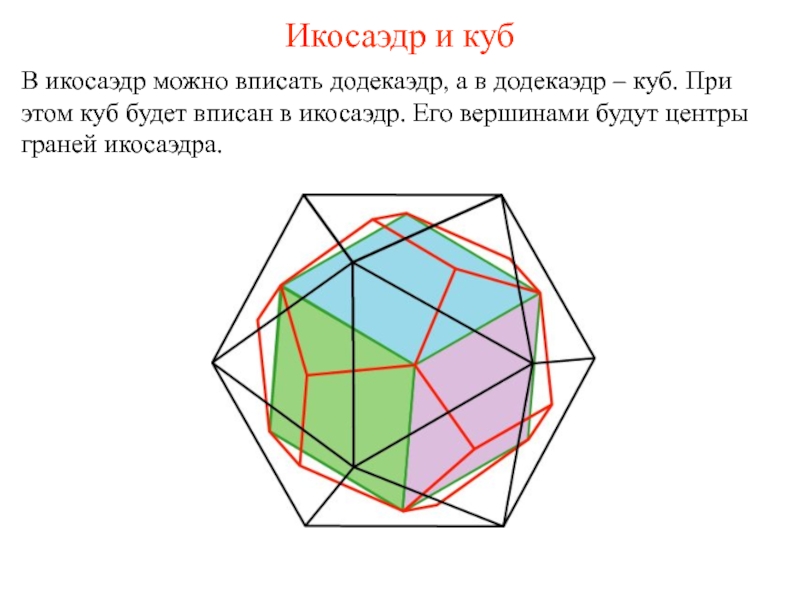
Слайд 20Икосаэдр и куб
В икосаэдр можно вписать додекаэдр, а в додекаэдр –
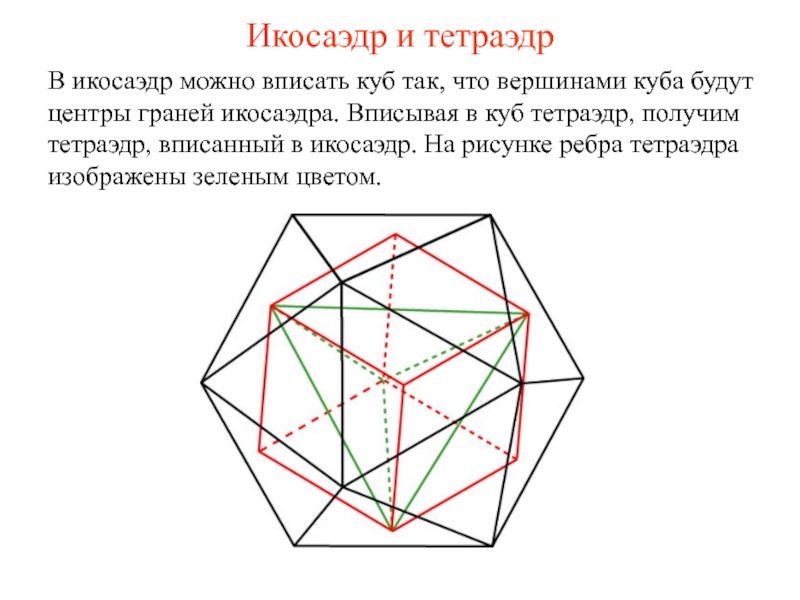
Слайд 22Икосаэдр и тетраэдр
В икосаэдр можно вписать куб так, что вершинами куба
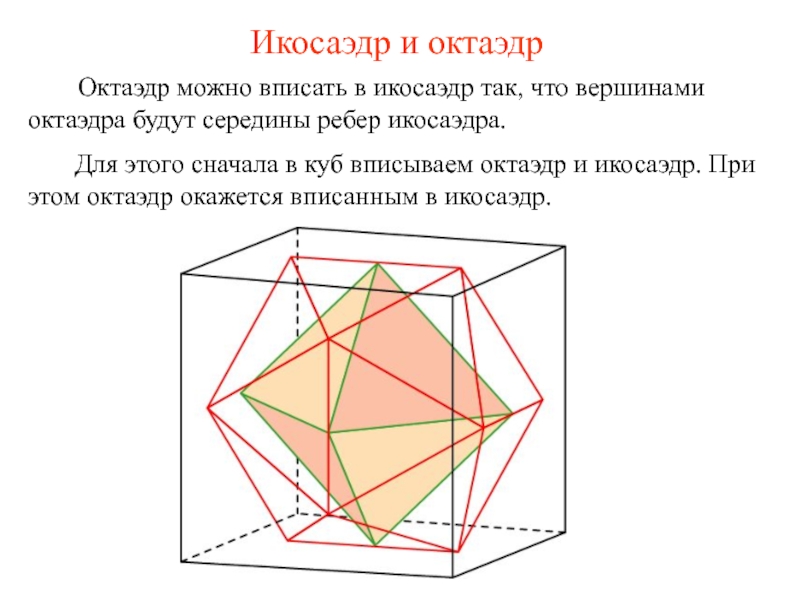
Слайд 24Икосаэдр и октаэдр
Октаэдр можно вписать в
Для этого сначала в куб вписываем октаэдр и икосаэдр. При этом октаэдр окажется вписанным в икосаэдр.
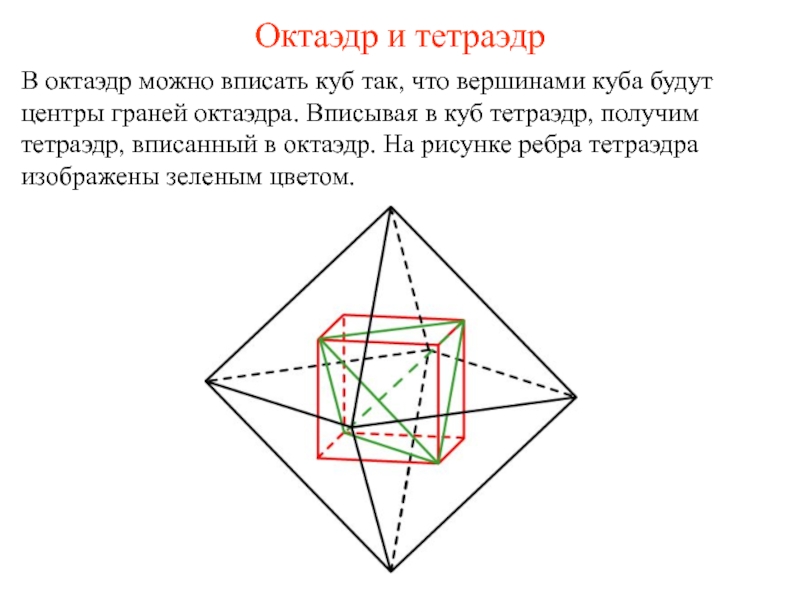
Слайд 26Октаэдр и тетраэдр
В октаэдр можно вписать куб так, что вершинами куба
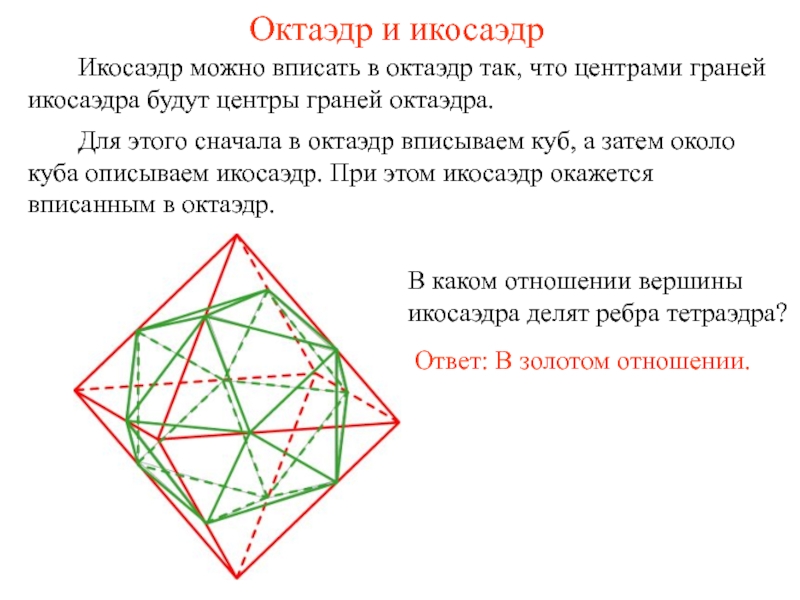
Слайд 28Октаэдр и икосаэдр
Икосаэдр можно вписать в
В каком отношении вершины икосаэдра делят ребра тетраэдра?
Ответ: В золотом отношении.
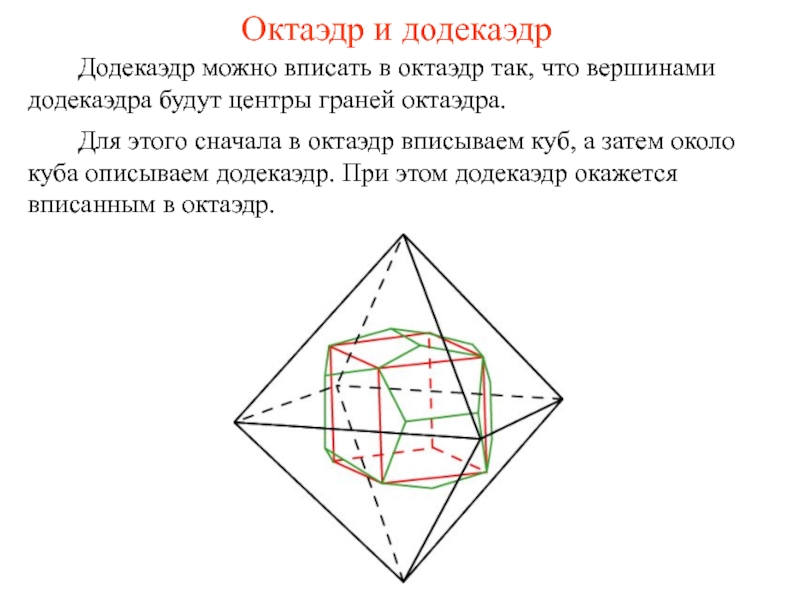
Слайд 30Октаэдр и додекаэдр
Додекаэдр можно вписать в
Слайд 32Тетраэдр и октаэдр
Октаэдр можно вписать в тетраэдр так, что вершинами октаэдра
Слайд 34Тетраэдр и куб
Впишем в тетраэдр октаэдр, а в октаэдр куб. Тогда
Слайд 36Тетраэдр и икосаэдр
Икосаэдр можно вписать в тетраэдр так, что центрами
Слайд 38Тетраэдр и додекаэдр
Впишем в тетраэдр октаэдр,
Слайд 40120 каскадов
В качестве первого можно взять один из пяти правильных многогранников.
На рисунке представлен каскад, в котором в качестве первого многогранника взят икосаэдр (красный), в него вписан додекаэдр (синий), затем куб (черный), далее тетраэдр (зеленый) и, наконец, октаэдр (розовый).
Рассмотренные случаи показывают, что в любой правильный многогранник можно вписать все остальные правильные многогранники. Последовательно вписывая друг в друга правильные многогранники, получим так называемое каскадное вписывание.