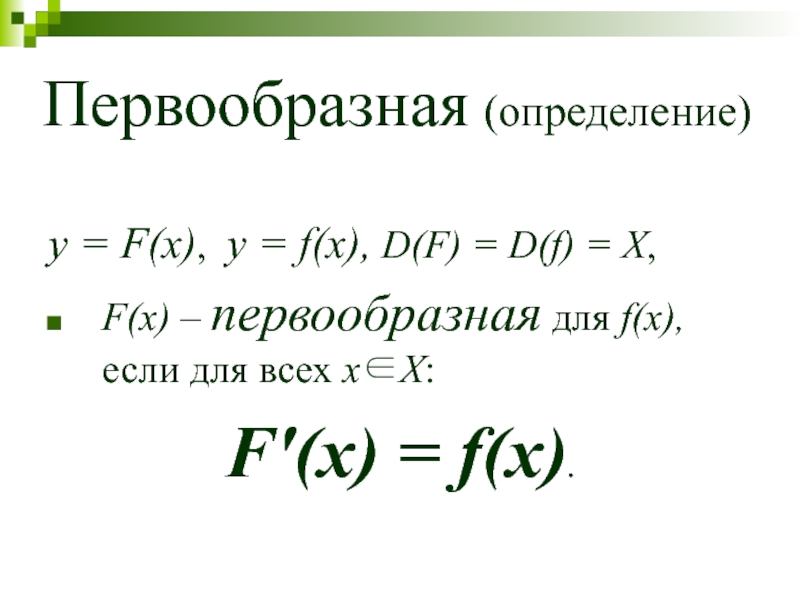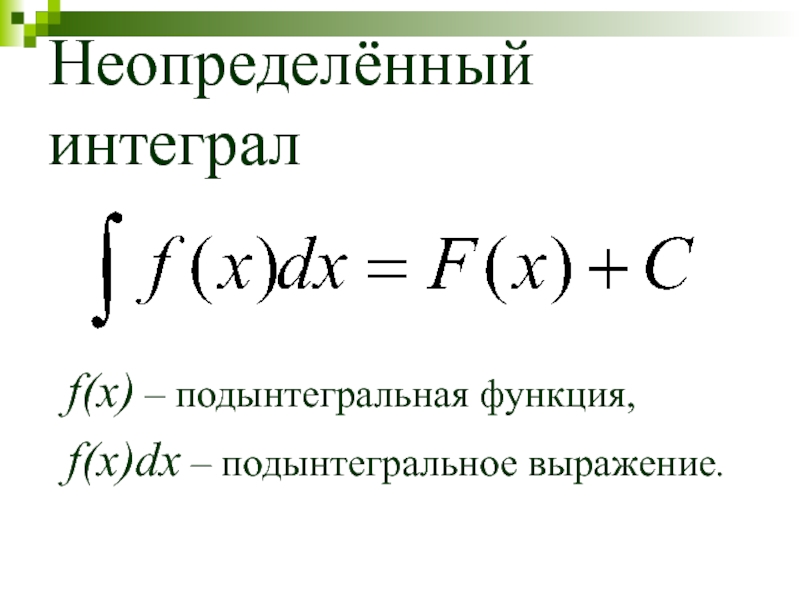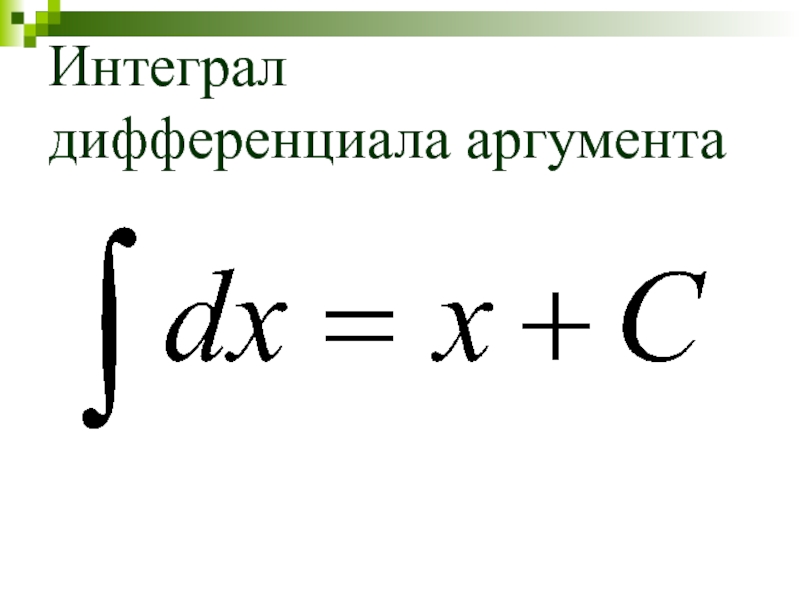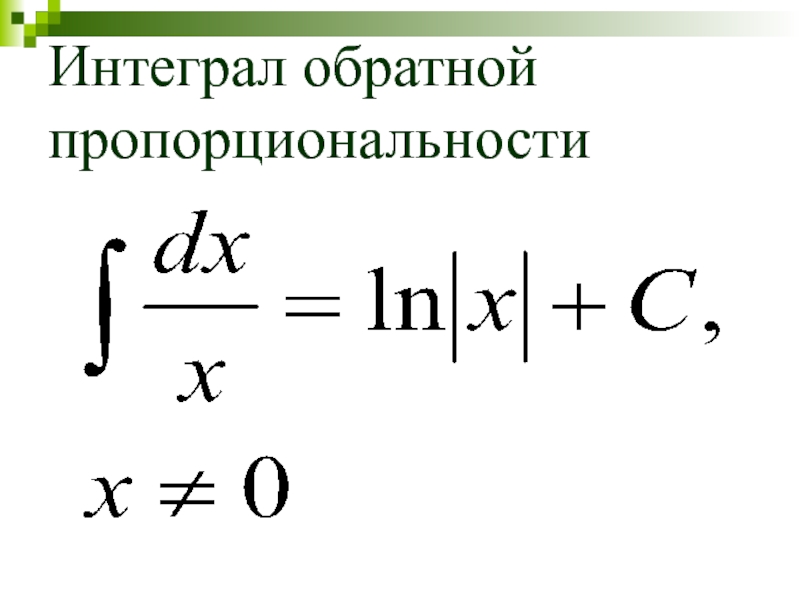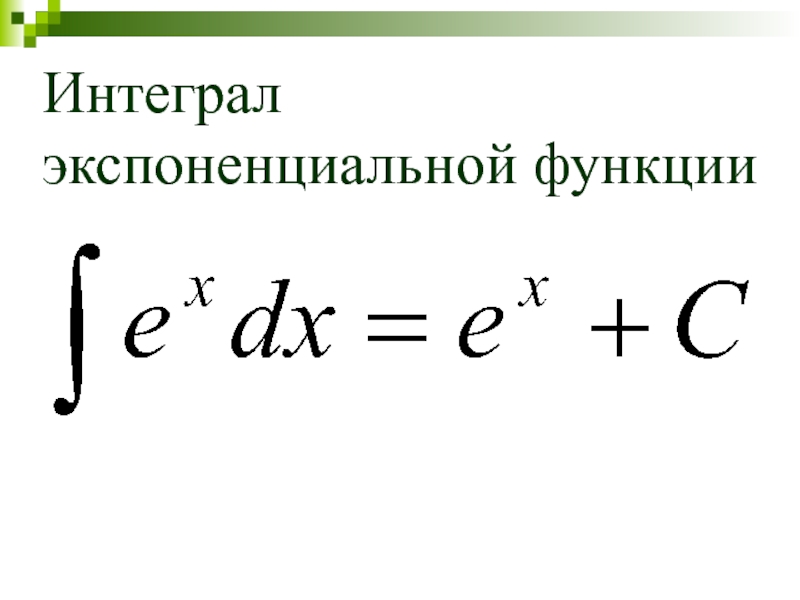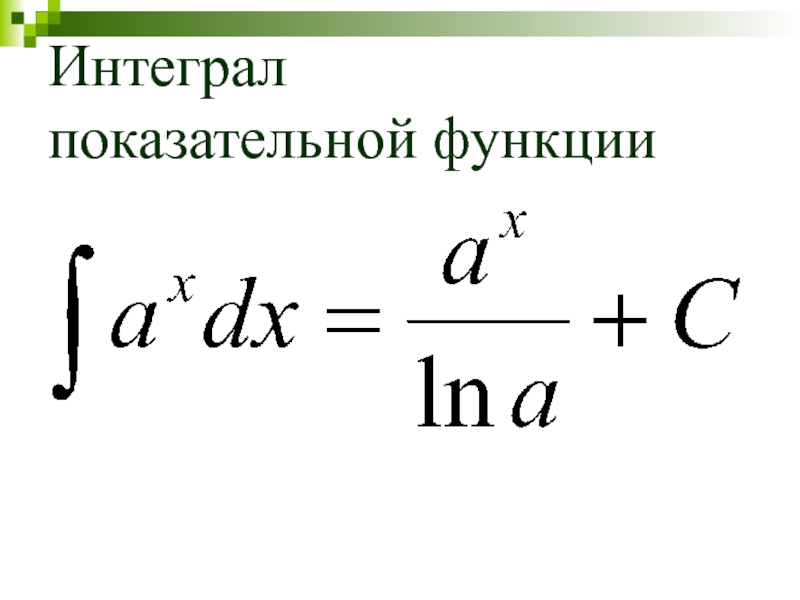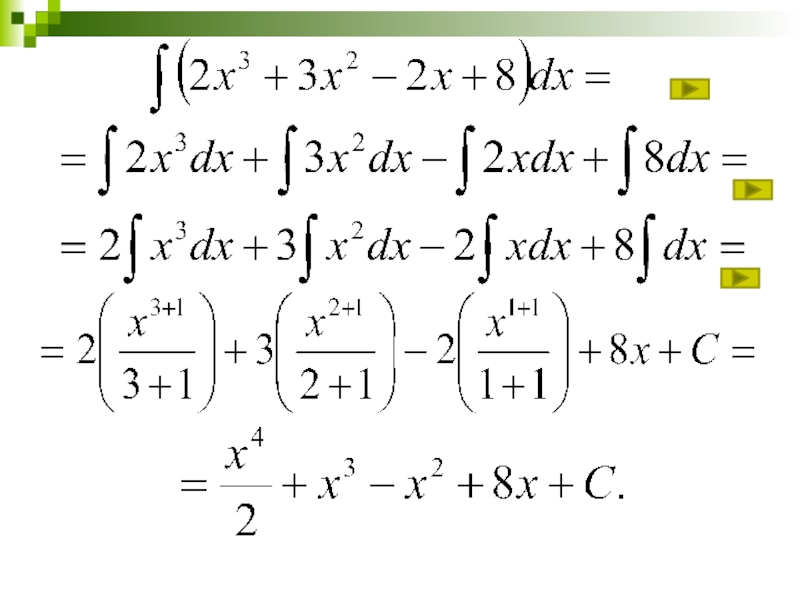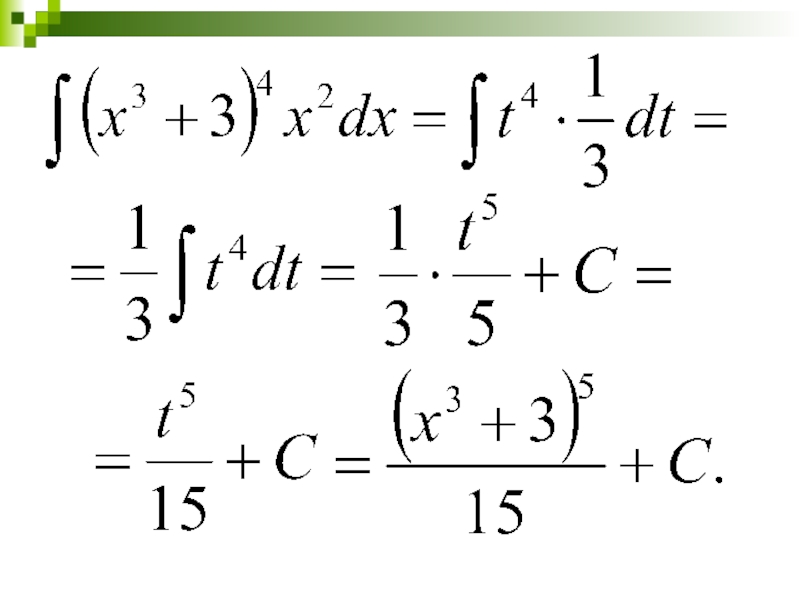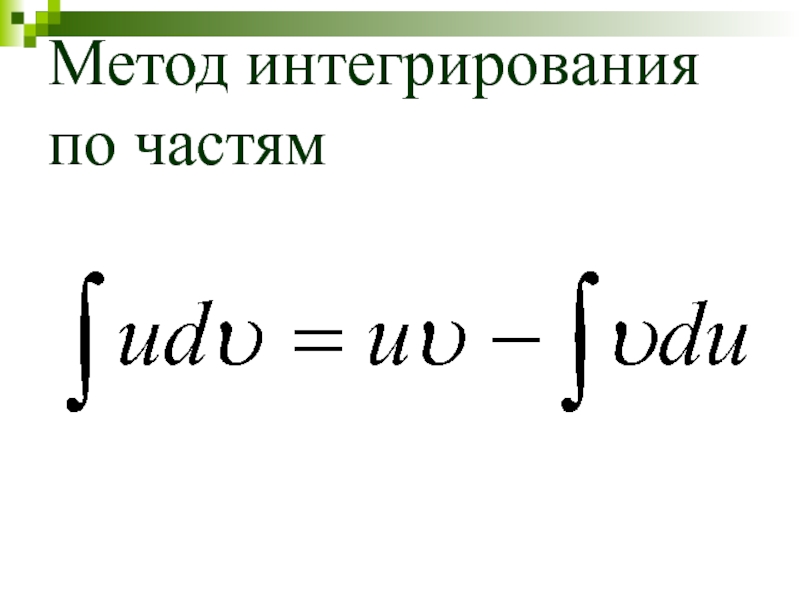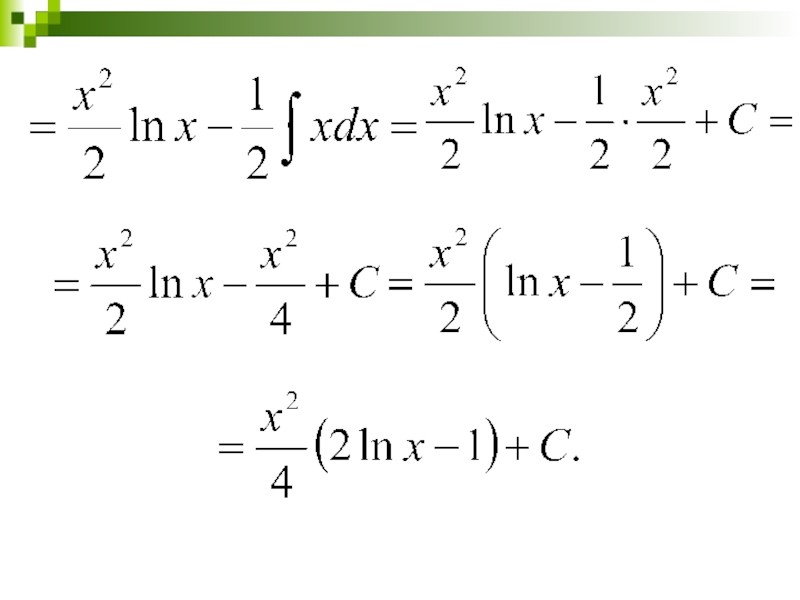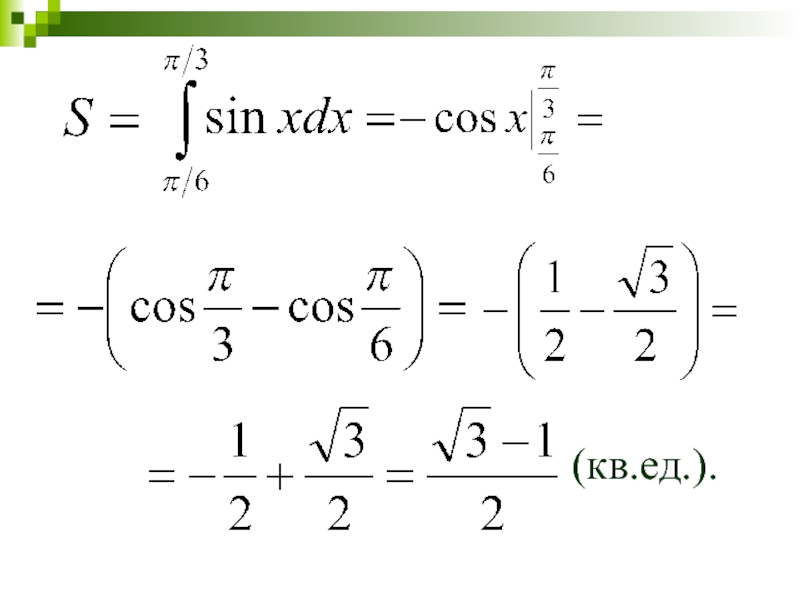- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Интегральное исчисление. Приложения определённого интеграла презентация
Содержание
- 1. Интегральное исчисление. Приложения определённого интеграла
- 2. Студент должен знать понятия неопределённого и определённого
- 3. Заполните таблицу
- 4. Первообразная (определение) y = F(x), y =
- 5. Определить первообразную функции f(x) = 3x2 F(x)
- 6. Определить первообразную функции f(x) = 3x2 1.
- 7. Теорема 1 Функция f(x), имеет бесконечное множество первообразных вида F(x)+С.
- 8. Неопределённый интеграл
- 9. Свойства неопределённого интеграла
- 10. Теорема 2
- 11. Теорема 3
- 12. Теорема 4
- 13. Теорема 5 Интеграл суммы равен сумме интегралов
- 14. Теорема 6
- 15. Основные формулы интегрирования
- 16. Интеграл дифференциала аргумента
- 17. Интеграл степенной функции
- 18. Интеграл обратной пропорциональности
- 19. Интеграл экспоненциальной функции
- 20. Интеграл показательной функции
- 21. Интеграл функции косинуса
- 22. Интеграл функции синуса
- 23. Методы интегрирования Непосредственное интегрирование Метод подстановки (замены переменной) Метод интегрирования по частям
- 24. Непосредственное интегрирование Найти:
- 26. Метод подстановки (замены переменной) Найти:
- 27. Введение подстановки
- 29. Метод интегрирования по частям
- 30. Найти: Чтобы воспользоваться формулой необходимо
- 31. Выберем функцию u и дифференциал dυ иначе:
- 32. Образец оформления
- 34. Определённый интеграл Определённый интеграл функции y=f(x) есть
- 35. Определённый интеграл f(x) – подынтегральная функция,
- 36. Формула Ньютона-Лейбница
- 37. Свойства определённого интеграла
- 38. Теорема 7 (аддитивность)
- 39. Теорема 8
- 40. Теорема 9
- 41. Теорема 10
- 42. Вычисление определённых интегралов Вычислить:
- 43. Вычисление определённых интегралов
- 44. Криволинейная трапеция плоская фигура, огра-ниченная линиями:
- 45. Площадь криволинейной трапеции
- 46. Вычисление площадей плоских фигур Вычислить площадь фигуры, ограниченной линиями:
- 47. (кв.ед.).
- 48. Дифференциальные уравнения
- 49. Дифференциальное уравнение* – это уравнение, связывающее
- 50. Решить ДУ – это значит, найти множество
- 51. Обыкновенное ДУ* – это ДУ, которое имеет
- 52. Порядок* ОДУ – это порядок старшей
- 53. Решение ОДУ ОДУ: y’ = x2; Одно
- 54. Общее решение ОДУ – это множество решений,
- 55. Частное решение ОДУ – одно из
- 56. Задача Коши – это задача нахождения частного решения дифференциального уравнения, удовлетворяющего заданным начальным условиям.
- 57. ОДУ с разделяющимися переменными – это уравнение,
- 58. Пример 1 Найти общее решение ОДУ
- 59. Этап 1: расшифровка производной Запишем:
- 60. Этап 2: разделение переменных x⋅dy/dx = y;
- 61. Этап 3: интегрирование Найдём интегралы левой и
- 62. Этап 4: нахождение y в явном виде
- 63. Пример 2 (задача Коши) Найти частное решение
- 64. Этап 1: расшифровка производной Запишем:
- 65. Этап 2: разделение переменных dy/dx = –2y;
- 66. Этап 3: интегрирование Найдём интегралы левой и
- 67. Этап 4: нахождение y в явном виде
- 68. Этап 5: нахождение частного решения Найдём частное
- 69. Итоги свойства интегралов; таблица неопределённых интегралов; методы интегрирования; формула Ньютона-Лейбница; дифференциальные уравнения; задача Коши.
- 70. Домашнее задание К практическому занятию №3: Теория
- 71. Благодарю за сотрудничество До встречи!
Студент должен знать понятия неопределённого и определённого интегралов; свойства интегралов; таблицу неопределённых интегралов; методы интегрирования; формулу Ньютона-Лейбница.
Слайд 2Студент должен знать
понятия неопределённого и определённого интегралов;
свойства интегралов;
таблицу неопределённых интегралов;
методы интегрирования;
формулу
Ньютона-Лейбница.
Слайд 4Первообразная (определение)
y = F(x), y = f(x), D(F) = D(f) =
X,
F(x) – первообразная для f(x), если для всех x∈Х:
F′(x) = f(x).
F(x) – первообразная для f(x), если для всех x∈Х:
F′(x) = f(x).
Слайд 6Определить первообразную функции f(x) = 3x2
1. F(x) = x3+1, т.к.
F′(x)
= (x3+1)′ = 3x2+0 = f(x).
2. F(x) = x3–7, т.к.
F′(x) = (x3–7)′ = 3x2–0 = f(x).
2. F(x) = x3–7, т.к.
F′(x) = (x3–7)′ = 3x2–0 = f(x).
Слайд 23Методы интегрирования
Непосредственное интегрирование
Метод подстановки (замены переменной)
Метод интегрирования по частям
Слайд 30Найти:
Чтобы воспользоваться формулой
необходимо выбрать функцию u и дифференциал dυ
Пусть
u = x и dυ = lnx.
Тогда: du = dx и
Такой выбор неудачен: невозможно интегрирование.
Слайд 34Определённый интеграл
Определённый интеграл функции y=f(x) есть число, значение которого зависит от
вида этой функции и пределов интегрирования a и b:
Слайд 35Определённый интеграл
f(x) – подынтегральная функция,
f(x)dx – подынтегральное выражение,
a –
нижний предел интегрирования
b – верхний предел интегрирования
b – верхний предел интегрирования
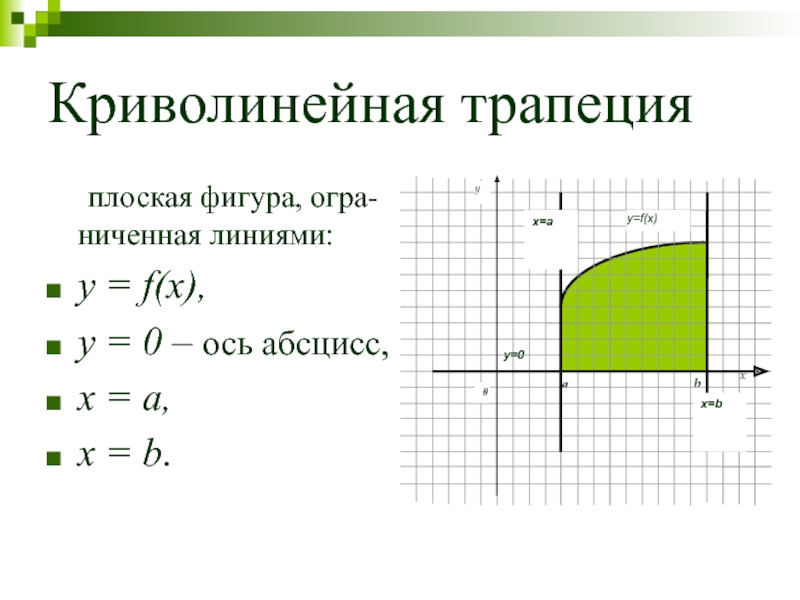
Слайд 44Криволинейная трапеция
плоская фигура, огра-ниченная линиями:
y = f(x),
y =
0 – ось абсцисс,
x = a,
x = b.
x = a,
x = b.
Слайд 49Дифференциальное уравнение* –
это уравнение, связывающее
независимую переменную x,
её функцию y,
производные
различных порядков этой функции: y’, y”, y’”…
*«Дифференциальное уравнение» будем кратко обозначать аббревиатурой «ДУ»
*«Дифференциальное уравнение» будем кратко обозначать аббревиатурой «ДУ»
Слайд 50Решить ДУ –
это значит, найти множество всех функций, которые удовлетворяют данному
ДУ:
Такое множество функций имеет вид:
y = f(x; C), где C – произвольная постоянная,
Это – общее решение ДУ.
Такое множество функций имеет вид:
y = f(x; C), где C – произвольная постоянная,
Это – общее решение ДУ.
Слайд 51Обыкновенное ДУ* –
это ДУ, которое имеет только одну независимую переменную (например,
х или t).
ДУ в частных производных** – это ДУ, которое имеет две и более независимых переменных.
*«Обыкновенное дифференциальное уравнение» будем кратко обозначать аббревиатурой «ОДУ».
**Такие ДУ в рамках нашей программы не рассматриваются.
ДУ в частных производных** – это ДУ, которое имеет две и более независимых переменных.
*«Обыкновенное дифференциальное уравнение» будем кратко обозначать аббревиатурой «ОДУ».
**Такие ДУ в рамках нашей программы не рассматриваются.
Слайд 52Порядок* ОДУ –
это порядок старшей производной:
y’ + 1 = 0
–
ОДУ первого порядка;
y” + y = x⋅sinx
y(V) + y(III) = a⋅y, a∈R
– ОДУ второго порядка;
– ОДУ пятого порядка.
*В рамках нашей программы будут рассматриваться только ОДУ первого порядка.
Слайд 53Решение ОДУ
ОДУ: y’ = x2;
Одно из решений: y = (1/3)⋅x3;
Проверка:
((1/3)⋅x3)’
= (1/3)⋅(x3)’ = (1/3)⋅3x2 = x2.
Другое решение ОДУ: y = (1/3)⋅x3 + 1,2.
ОДУ могут иметь множество решений.
Другое решение ОДУ: y = (1/3)⋅x3 + 1,2.
ОДУ могут иметь множество решений.
Слайд 54Общее решение ОДУ –
это множество решений, содержащее ВСЕ без исключения решения
этого дифференциального уравнения.
Слайд 55Частное решение ОДУ –
одно из множества решений ОДУ, удовлетворяющее изначально
заданным дополнительным условиям:
ОДУ: y’ = x2, y(1) = 1;
Общее решение: y(x) = (1/3)⋅x3 + С.
Найдём С: 1 = (1/3)⋅13 + С
С = 2/3.
Частное решение ОДУ: y = (1/3)⋅x3 + 2/3.
ОДУ: y’ = x2, y(1) = 1;
Общее решение: y(x) = (1/3)⋅x3 + С.
Найдём С: 1 = (1/3)⋅13 + С
С = 2/3.
Частное решение ОДУ: y = (1/3)⋅x3 + 2/3.
Слайд 56Задача Коши –
это задача нахождения частного решения дифференциального уравнения, удовлетворяющего заданным
начальным условиям.
Слайд 57ОДУ с разделяющимися переменными –
это уравнение, которое возможно преобразовать таким образом,
что правая часть будет содержать выражения только с переменной y, а левая – только с переменной х (или наоборот).
Слайд 60Этап 2: разделение переменных
x⋅dy/dx = y;
По свойству пропорции, перенесём «крест-накрест»
х и dx вправо, а y – влево:
dy/y = dх/x;
dy/y = dх/x;
Слайд 61Этап 3: интегрирование
Найдём интегралы левой и правой частей уравнения:
∫(dy/y) =
∫(dх/x);
ln|y| = ln|x| + константа;
константа = ln|С|;
ln|y| = ln|x| + ln|С|;
ln|y| = ln|x| + константа;
константа = ln|С|;
ln|y| = ln|x| + ln|С|;
Слайд 62Этап 4: нахождение y в явном виде
Найдём общее решение (функцию y)
в явном виде:
ln|y| = ln|x| + ln|С|;
ln|y| = ln|Cx|;
y = Сx.
Ответ: y = Сx, где С – константа.
ln|y| = ln|x| + ln|С|;
ln|y| = ln|Cx|;
y = Сx.
Ответ: y = Сx, где С – константа.
*Общее решение ОДУ – семейство функций (здесь – семейство прямых пропорциональностей).
Слайд 63Пример 2 (задача Коши)
Найти частное решение дифференциального уравнения
y’ = –2y,
удовлетворяющее
начальному условию
y(0) = 2.
y(0) = 2.
Слайд 65Этап 2: разделение переменных
dy/dx = –2y;
По свойству пропорции, перенесём «крест-накрест» dx
вправо, а y – влево:
dy/y = –2dх;
dy/y = –2dх;
Слайд 66Этап 3: интегрирование
Найдём интегралы левой и правой частей уравнения:
dy/y =
dх;
∫(dy/y) = ∫(–2dх);
∫(dy/y) = –2∫dх;
ln|y| = –2x + С`;
∫(dy/y) = ∫(–2dх);
∫(dy/y) = –2∫dх;
ln|y| = –2x + С`;
Слайд 67Этап 4: нахождение y в явном виде
Найдём общее решение (функцию y)
в явном виде:
ln|y| = –2x + С`;
Учтём: если lna = b, то a = eb;
y = e–2x + С`;
y = eС`⋅ e–2x ⇒
Переобозначим: eС` = С,
тогда общее решение будет иметь вид: y = Сe–2x.
(семейство экспоненциальных функций)
ln|y| = –2x + С`;
Учтём: если lna = b, то a = eb;
y = e–2x + С`;
y = eС`⋅ e–2x ⇒
Переобозначим: eС` = С,
тогда общее решение будет иметь вид: y = Сe–2x.
(семейство экспоненциальных функций)
Слайд 68Этап 5: нахождение частного решения
Найдём частное решение для y(0) = 2:
При х = 0: y = Сe–2⋅ 0 = Сe0 = С⋅ 1 = С = 2.
Тогда y = Сe–2x и С = 2 ⇒
y = 2e–2x – частное решение ОДУ.
Ответ: y = 2e–2x.
Слайд 69Итоги
свойства интегралов;
таблица неопределённых интегралов;
методы интегрирования;
формула Ньютона-Лейбница;
дифференциальные уравнения;
задача Коши.
Слайд 70Домашнее задание
К практическому занятию №3:
Теория – лекционный материал;
Письменно – упражнения для
самостоятельной работы.
